If v=u2, in which direction the man should swim so that his drift along the flow is minimum and find value of the minimum drift.
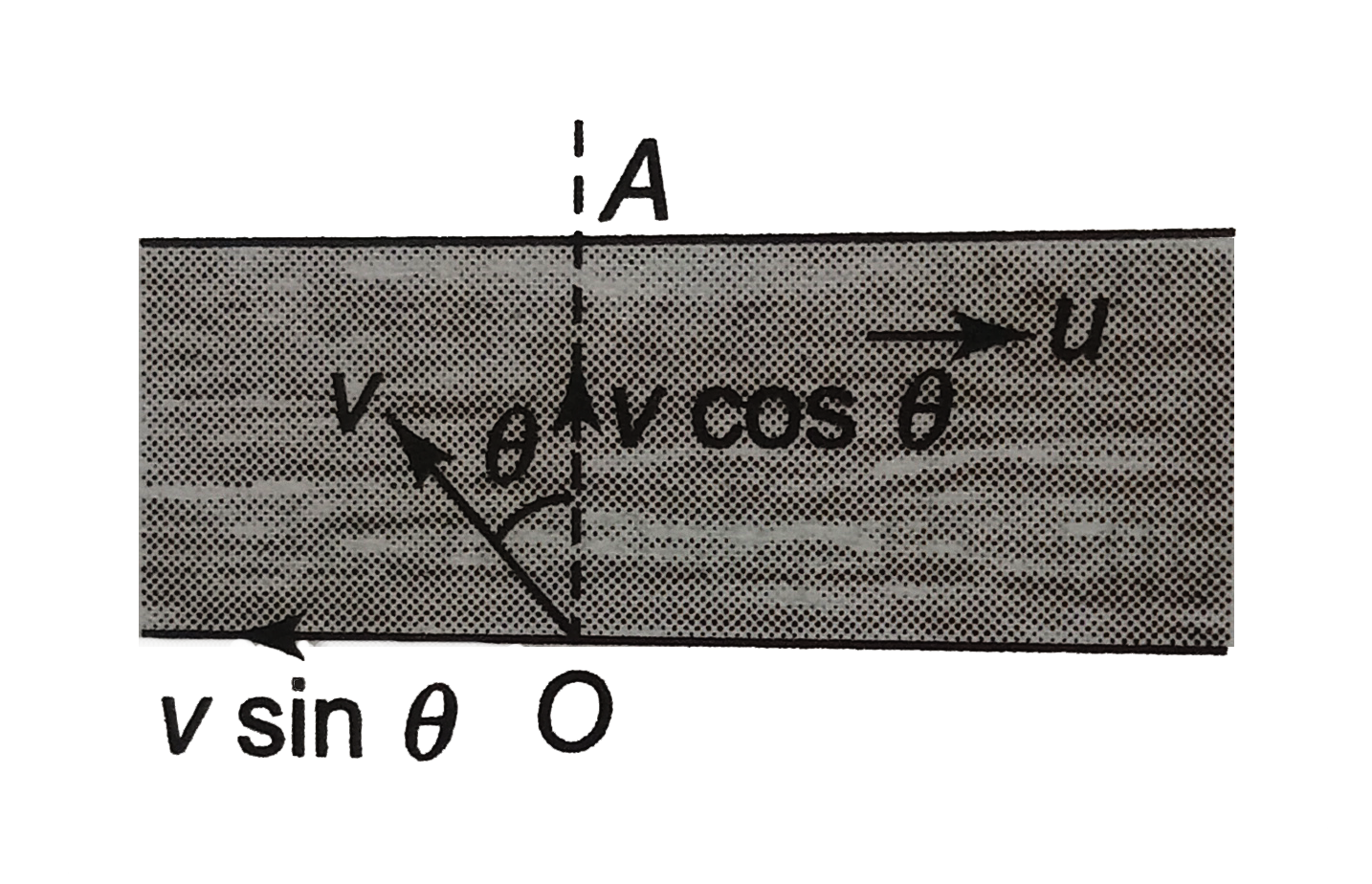
(vm/g)x=vsinθ−u=u2sinθ−u
(vm/g)y=vcosθ=u2cosθ
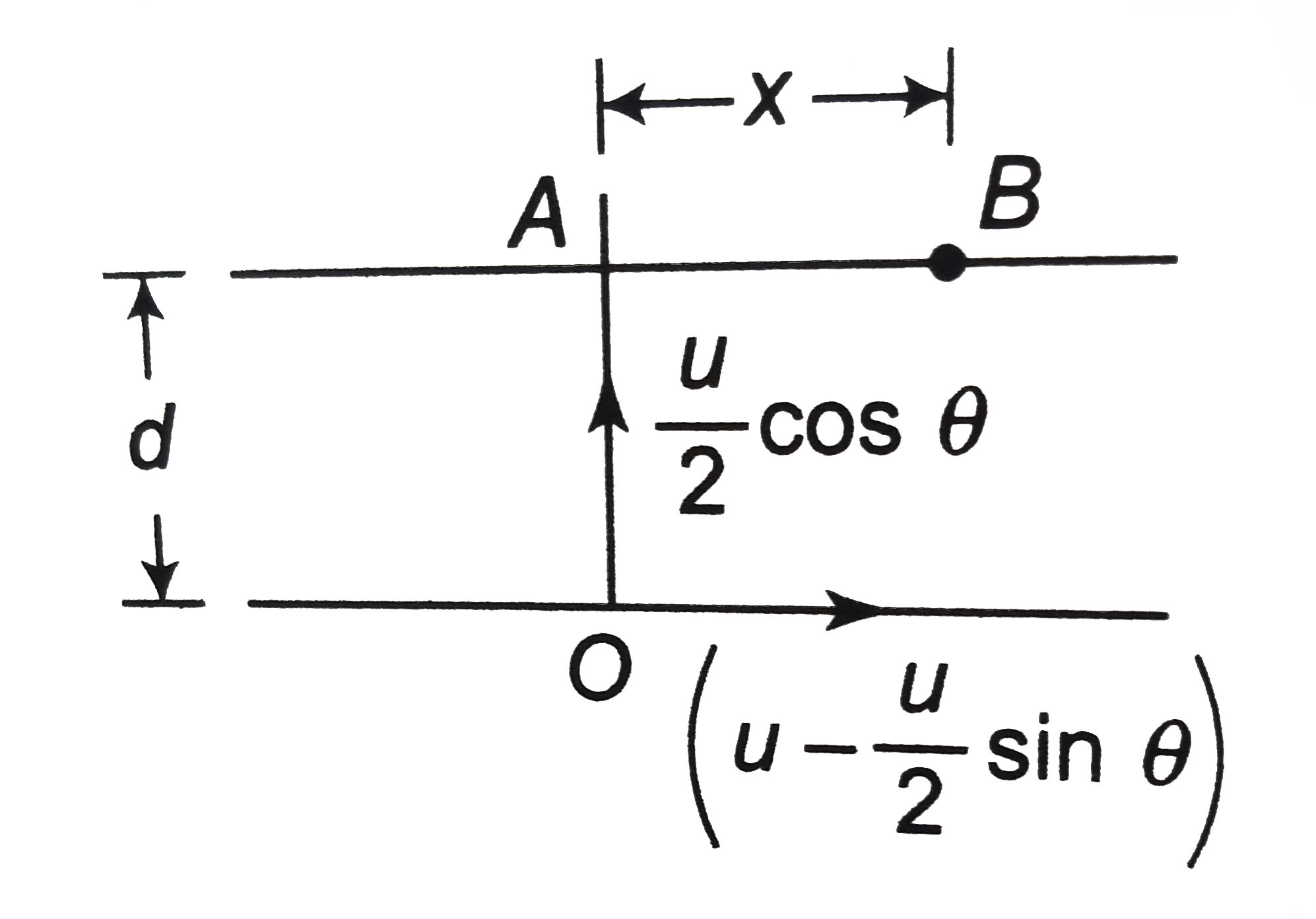
y:d=u2cosθt⇒t=2ducosθ
x:x=(u−u2sinθ)t=(u−u2sinθ)2ducosθ
=2d(secθ−tanθ2)
For x to be minimum
dxdθ=(secθtanθ−12sec2θ)=0
secθ=2tanθ
1cosθ=2sinθcosθ⇒sinθ=12⇒θ=30∘
xmin=2d(sec30∘−tan30∘2)
2d(2√3−12√3)=2d(4−12√3)=√3d
Topper's Solved these Questions
Similar Questions
Find minimum value of (9−x)(2−x)
View SolutionA man can swim in still water with a speed v . River flows at a speed u which is greater than the swimming speed (v) of the man . Explain that the man cannot move perpendicular to the flow . If man swims at an angle θ with the river flow , then find drift along the flow by the time he crosses the river . Also find the minimum value of the drift along the flow x by the time he crosses the river .
View Solution
Knowledge Check
Find the minimum value of sin2x
A-1B0C1D1/2A boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
A30∘B60∘C150∘D120∘A river is flowing from west to east with a speed of 5m/min. A man can swim in still water with a velocity 10m/min. In which direction should the man swim so as to take the shortest possible path to go to the south.
A30∘ with downstreamB60∘ with downstreamC120∘ with downstreamDSouth
In the previous problem, the man wants to cross the river in the minimum time. In which directions, he should move? Find the minimum time to cross the river and his displacement (drift) along the flow.
View SolutionA man swimming in a river from a point. A on one bank has to reach a point C on other bank, which is at a distance l from the point B, directly opposite to A on other bank. River width is d and the current velocity is u0. Find the minimum speed of swimmer relative to still water with which he should swim.
View SolutionA river is flowing from the west to the east at 5m/min. A swimmer on the southerm bank can swim at 10 m/min in still water. In what direction should he swim if (i) He wishes to cross the river in minimum time (ii) He wishes to cross te river through shortest route
View SolutionA block of mass m rests on a horizontal floor for which coefficient of friction is μ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.
View SolutionA river is flowing at a speed of 5 km/h in a particular direction. A man, who can swim at a speed of 20 km/h in still water, starts swimming along the direction of flow of the river from point A and reaches another point B which is at a distance of 30 km from the starting point A. On reaching point B, the man turns back and starts swimming against the direction of flow of the river and stops after reaching point A. The total time taken by the man to complete his journey is
View Solution
