If X represents force, Y represents area and Z represents time. The quantities having same dimensions as coefficient of viscosity in are
XYZ
XZY
YZX
XYZ
The correct Answer is:B
To find the quantities having the same dimensions as the coefficient of viscosity, we can start by recalling the definition and formula for the coefficient of viscosity (η).
1. Understanding the Coefficient of Viscosity:
The coefficient of viscosity (η) is defined in the context of Newton's law of viscosity, which states that the shear stress (τ) is proportional to the shear rate (du/dy). The formula can be expressed as:
τ=ηdudy
2. Relating Shear Stress and Shear Rate:
Shear stress (τ) is defined as force (F) per unit area (A):
τ=FA
Therefore, we can rewrite the equation for shear stress in terms of force and area:
FA=ηdudy
3. Rearranging for Coefficient of Viscosity:
Rearranging the equation gives us:
η=FA⋅dydu
4. Substituting Dimensions:
- Force (F) has dimensions of (MLT−2)
- Area (A) has dimensions of (L2)
- The shear rate dudy has dimensions of (T−1) since it is a velocity gradient (change in velocity over change in distance).
5. Calculating Dimensions of η:
Plugging in the dimensions into the equation:
η=(MLT−2)(L2)⋅(T−1)=(ML−1T−1)
6. Conclusion:
The dimensions of the coefficient of viscosity (η) are (ML−1T−1). Thus, any quantity that has the same dimensions as (ML−1T−1) will be equivalent to the coefficient of viscosity.
The coefficient of viscosity (η) is defined in the context of Newton's law of viscosity, which states that the shear stress (τ) is proportional to the shear rate (du/dy). The formula can be expressed as:
τ=ηdudy
Shear stress (τ) is defined as force (F) per unit area (A):
τ=FA
Therefore, we can rewrite the equation for shear stress in terms of force and area:
FA=ηdudy
Rearranging the equation gives us:
η=FA⋅dydu
- Force (F) has dimensions of (MLT−2)
- Area (A) has dimensions of (L2)
- The shear rate dudy has dimensions of (T−1) since it is a velocity gradient (change in velocity over change in distance).
Plugging in the dimensions into the equation:
η=(MLT−2)(L2)⋅(T−1)=(ML−1T−1)
The dimensions of the coefficient of viscosity (η) are (ML−1T−1). Thus, any quantity that has the same dimensions as (ML−1T−1) will be equivalent to the coefficient of viscosity.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (JEE (Main) & Other State Boards For Engineering Entrance)
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Numerical Problems)
28 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Knowledge Check
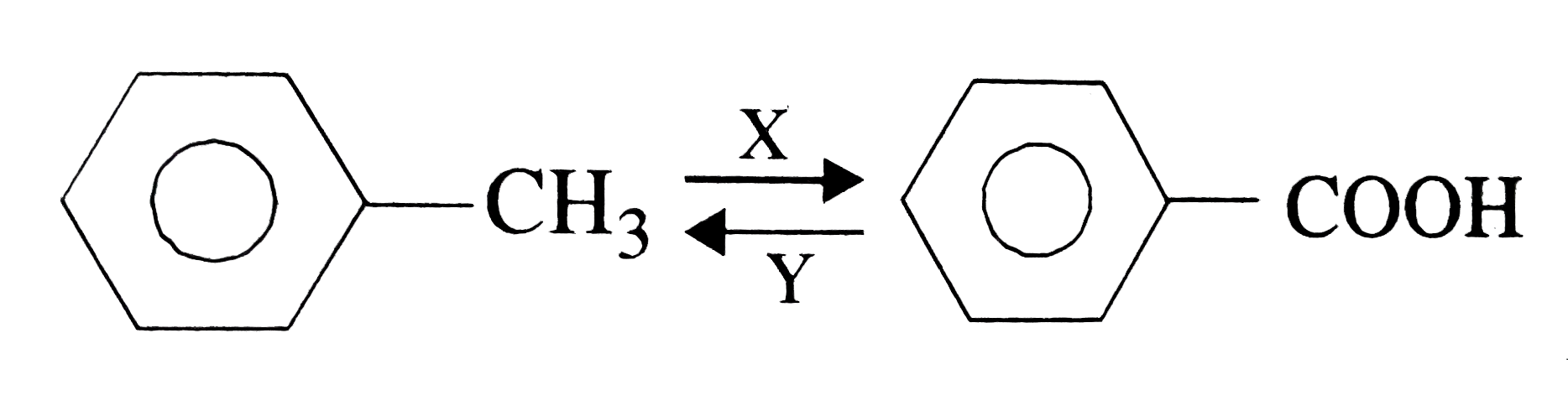 X and Y representAH2/Pt,KMnO4BKMnO4,H2/PtCKMnO4/KOH/HI/PDNH2−NH2/KOH,HI/P
X and Y representAH2/Pt,KMnO4BKMnO4,H2/PtCKMnO4/KOH/HI/PDNH2−NH2/KOH,HI/PWhich one of the following represents the correct dimensions of the coefficient of viscosity?
A(a) ML−1T−1B(b) MLT−1C( c ) ML−1T−2D(d) ML−2T−2Which one of the following represents the correct dimensions of the coefficient of viscosity?
A[ML−1T−2]B[MLT−1]C[ML−1T−1]D[ML−2T−2]
Area under force-displacement curve represents
View SolutionIn space 2y+3z=0 represents
View SolutionWhich measurement represents the smallest quantity?
View SolutionConsider an expression F=Axsin−1'(Bt) where F represents force, x represents distance and t represents time. Dimensionally the quantity AB represents
View SolutionArea under Force-Displacement curve represents
View Solution
