Image of an object kept on the principal axis of transparent sphere with silvered rear surface
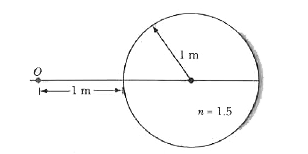
A sphere of radius 1m and n=1.5 is silvered at its back. A point objet is kept at a distance of 1m from the front face (Fig. 34-30). Where will the final image be formed ?
Here , we can clearly see that there will be three events before the final image will be formed. Refraction, reflection , and refraction back into the air.
Calculation : For the first event O is the optical center, n1=1 , n2=1.5, u=−1m , R=+1m. Therefore, we get
1.5v1−1−1=1.5−11
v1=3m
This image will act as an object for the rear silvered surface . However, for taking the object distance, we have to measure it from the pole of the mirror. As we have discussed before,
u2=v1−x
u2=−3−2=−5m
Applying mirror formula, we get (radius of curvature is −1m, so final length of the mirror is −1/2m)
1v2+1−5=1−0.5
v2=−59m.
These reflected rays will again be refracted from the spherical surface . Since now The direction of the light rays has reversed, therefore
u3=−v2−x
u3=−(−59)−2=−139m.
This can be seen from Fig. 35-29 also. Now,
1v3−1.5−139=1−1.5−1=0.5
Note here that the radius of this surface is negative becuase the direction of the incident rays has reversed. Solving we get v3=−13/7m.
Negative means that the image is virtual formed inside the spherical surface. This is distance from the left edge of the spherical surface.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point6videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems44videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)4videos
GRAVITATION
Similar Questions
There is a glass (μ=1.5) biconvex lens of radius of curvature 5 cm and thickness of the lens is also 5 cm. An object is placed at a distance 20 cm from the front surface of lens. Locate its final image.
View SolutionA plane mirror is made of glass slab (μg=1.5) 2.5 cm thick and silvered on back. A point object is placed 5 cm in front of the unsilvered face of the mirror. What will be the position of final image ?
View Solution
Knowledge Check
- Question 1 - Select One
A plane mirror is made of glass slab (μg=1.5) 2.5 cm thick and silvered on back. A point object is placed 5 cm in front of the unsilvered face of the mirror. What will be the position of final image ?
A12 cm from unsilvered faceB14.6 cm from unsilvered faceC5.67 cm from unsilvered faceD8.33 cm from unsilvered - Question 2 - Select One
A convex mirror of radius of curvature 1.6m has an object placed at a distance of 1m from it. The image is formed at a distance of
A8/13m in fron of the mirrorB8/13m behind the mirrorC4/9 m in front of the mirrorD4/9m behind the mirror - Question 3 - Select One
A point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
A6cmB4cmC12cmD9cm
A convex mirror of radius of curvature 1.6m has an object placed at a distance of 1m from it. The image is formed at a distance of
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
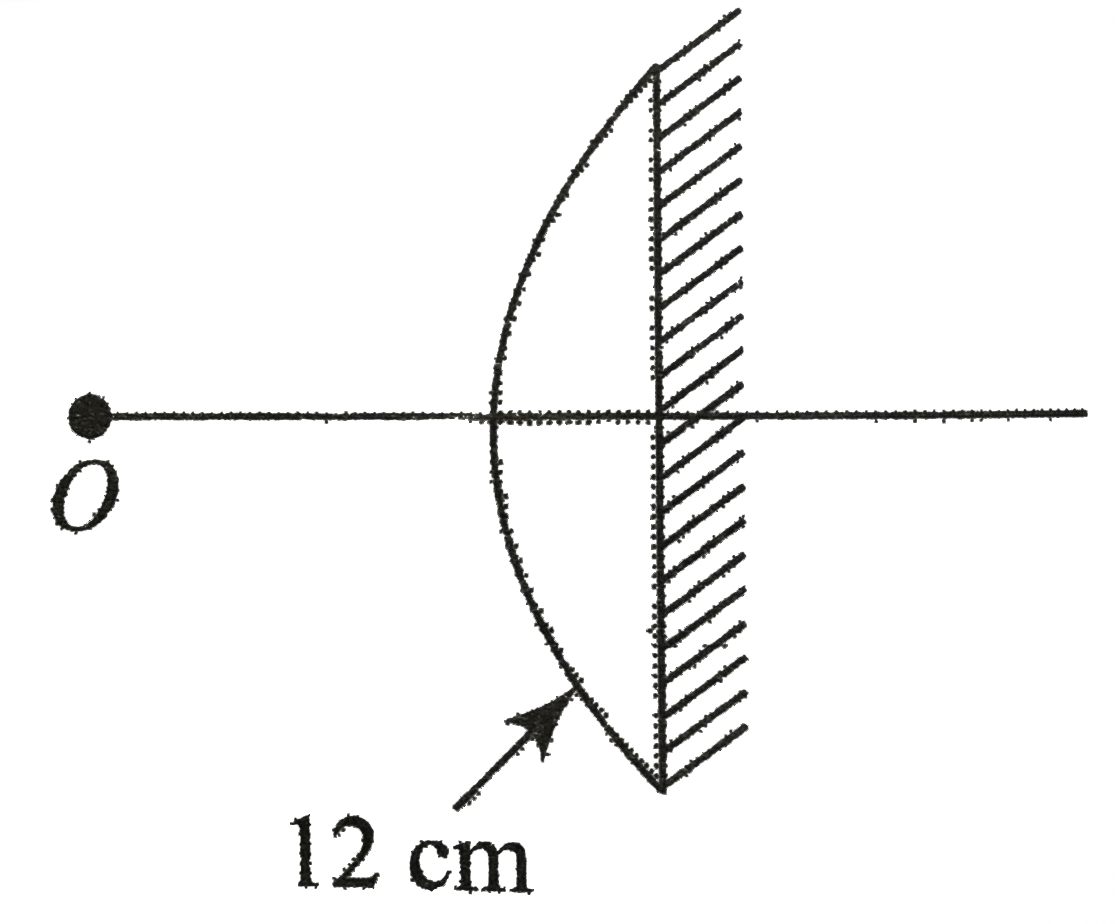
View SolutionA plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
 View Solution
View SolutionA plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
 View Solution
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View Solution

