Question

There is a glass $(\mu =1.5)$ biconvex lens of radius of curvature 5 cm and thickness of the lens is also 5 cm. An object is placed at a distance 20 cm from the front surface of lens. Locate its final image.

Explanation

Since lens is thick so we cannot use lens formula. We can use refraction formula to locate the final image. Refraction formula is given as follows :
`(mu_(2))/(v)-(mu_(1))/(u)=(mu_(2)-mu_(1))/(R )`

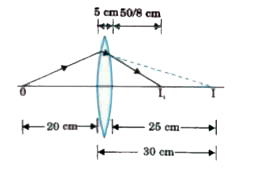
But note that there are two refractions which are taking place here. First refraction is from air into glass into air to form the final image. Image of the first refraction will act as object for the second refraction but only after the adjustment of thickness of lens.
Let us apply formula for the first refraction.
`(1.5)/(v)-(1)/((-20))=(1.5-1)/(+5)`
`rArr" "(1.5)/(v)+(1)/(20)=(1)/(10)`
`rArr" "(1.5)/(v)=(1)/(10)-(1)/(20)=(1)/(20)`
`rArr" "v=30cm`
So real image is formed on the other side of surface at a distance 30 cm from it. Next surface of lens is 5 cm ahead. Hence, the first image is formed at a distance 25 cm ahead of second surface. So for the second refraction this image is one virtual object kept at a distance 25 cm from it. Distance of the virtual object as per sign convention is positive.
`u=+25cm`.
`(mu_(2))/(v)-(mu_(1))/(u)=(mu_(2)-mu_(1))/(R )`
`rArr" "(1)/(v)-(1.5)/(+25)=(1-1.5)/(-5)`
`rArr" "(1)/(v)=(3)/(50)+(1)/(10)`
`rArr" "(1)/(v)=(8)/(50)`
`rArr" "v=(50)/(8)cm=6.25cm`
Hence final image is formed at a distance 6.25 cm from the rear surface of lens. And the image is real.