Impact Parameter
Impact parameter of a charged particle is the perpendicular distance of the velocity vector of the particle from the centre of the nucleus, when it is far away from the atom.
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - MBD -HARYANA BOARDCHAPTER - ATOMS AND NUCLEIEXERCISE - SHORT ANSWER TYPE QUESTIONS
44 Videos
- ATOMS AND NUCLEIBOOK - MBD -HARYANA BOARDCHAPTER - ATOMS AND NUCLEIEXERCISE - LONG ANSWER TYPE QUESTIONS
3 Videos
- BOARD QUESTION PAPER (SOLVED) - 2019BOOK - MBD -HARYANA BOARDCHAPTER - BOARD QUESTION PAPER (SOLVED) - 2019EXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
Similar Questions
A dparticle of mas m moving with speed u collides elastically with a sphere of radius R and same mass at rest, at an impact parameter d. Find
(a) Angle between their final velocities and
(b) Magpitude of their final velocities.
View SolutionFigure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
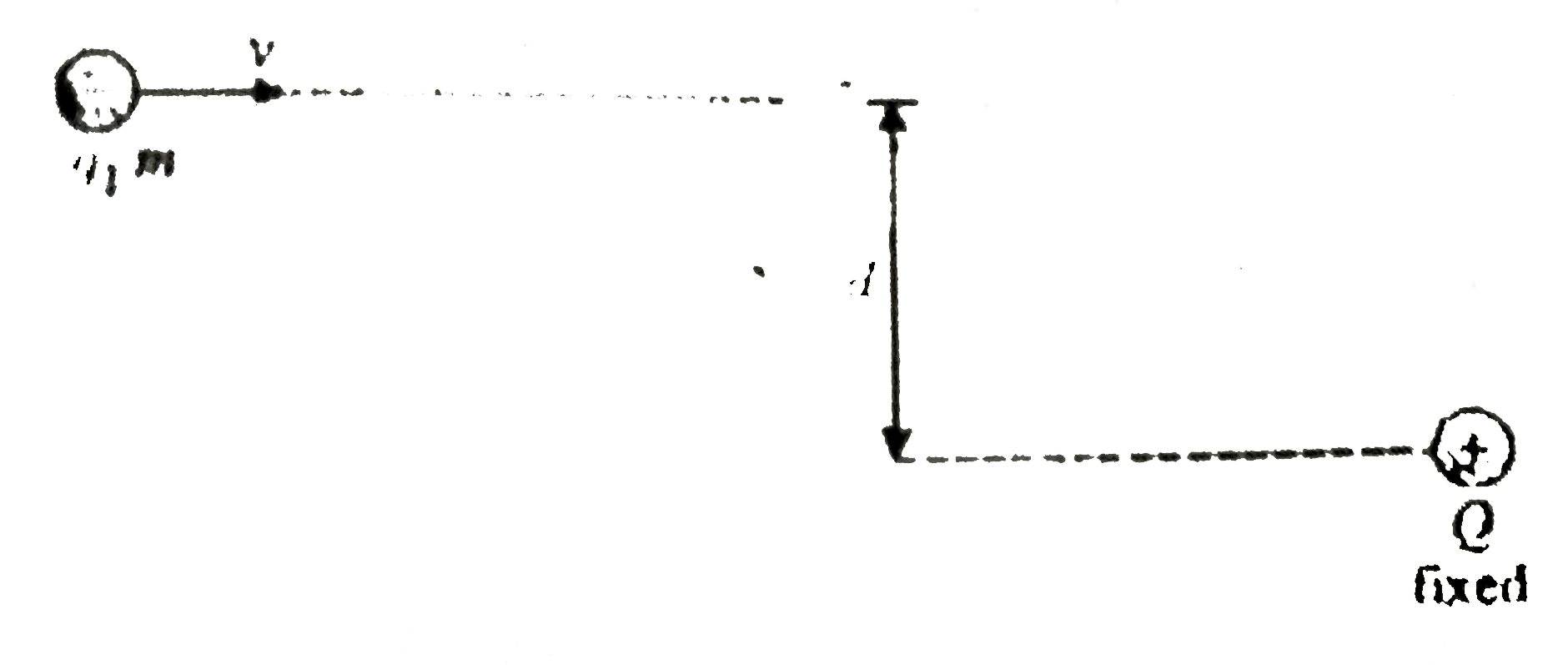
View Solution
Knowledge Check
(A) the trajetory traced by an incident particle depends on the impact parameter of collision.
(R) the impact parameter is the perpendicular distance of the initial velocity vector of the incident particle from the centre of the target nucleus.Aif both assertion and reason are true and reason is the correct explanation of assertion.Bif both assertion and reason are true but reason is not the correct explanation of assertion.Cif assertion is true but reason is false.Dif both assertion and reason are false.A proton of mass m moving with a speed v0 apporoches a stationary proton that is free to move. Assuming impact parameter to be zero., i.e., head-on collision. How close will be incident proton go to other proton ?
Ae3πε0m2v0Be3πε0mv0Ce2πε0mv20DNone of theseA disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
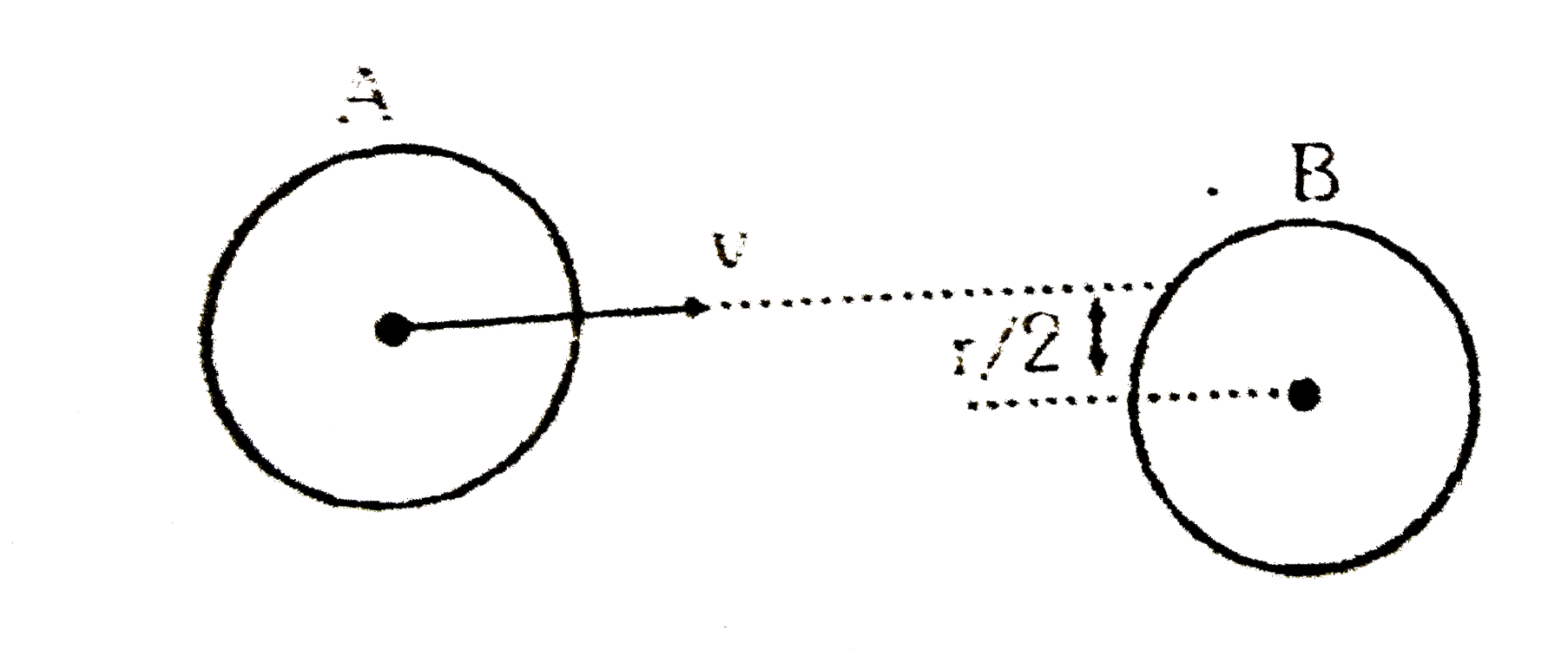 A√154vBv4Cv2D√3v2
A√154vBv4Cv2D√3v2
A disk of radius r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk. Express the magnitude and the direction of the velocity of each of tho disks after the collision, as a function of tho impact parameter d (Fig. 10.7a). Calculatious to be made only for the nonrelativistic approximation.
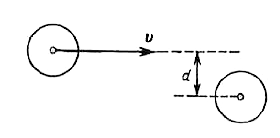
View SolutionA projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach r0.
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
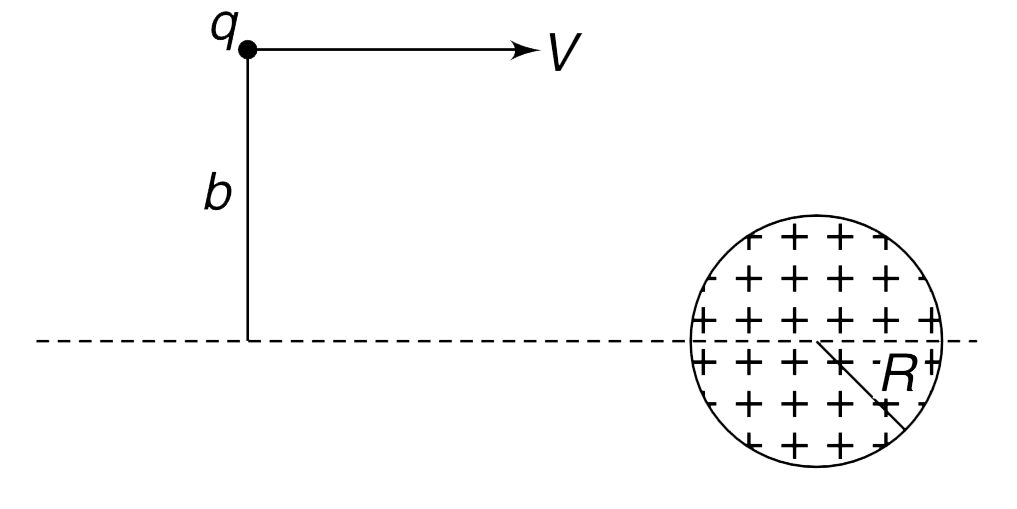
View SolutionOn a horizontal smooth surface a disc is placed at rest. Another disc of same mass is coming with impact parameter equal to its own radius. First disc is of radius r. What should be the radius of comping disc so that after collision first disc moves at an angle 45∘ to the direction of motion of incoming disc ?
View SolutionThe following text gives a qualitative idea about Rutherford's α− particle scattering experiment.

Applying some trigonometry and calculus, Rutherford got the following equation:
cot(02)=K×(KE)Ze2×b
where,K=constant=(19×10)c2N−m2
KE = initial kinetic energy of α−particle,
e=1.6×10−19C
In an experment with gold nucleus (assume Z=80) with impact parameter equal to 10−4m the scattering angle was found to be 90∘, What should be the initial KE of α−particle?
View Solution
