In a bicycle the radius of rear wheel is twice the radius of front wheel. If vF and vr are the speeds of top most points of front and rear wheels respectively, then :
vr=2vF
vF=2vr
vF=vr
vF>vr
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the speeds of the topmost points of the front and rear wheels of the bicycle based on their radii.
1. Identify the Radii of the Wheels:
- Let the radius of the front wheel be R.
- Then, the radius of the rear wheel will be 2R (as given in the problem).
2. Understand the Relationship Between Linear Speed and Angular Speed:
- The linear speed v of a point on the circumference of a wheel is related to its angular speed ω and radius r by the equation:
v=r⋅ω
- Thus, for the front wheel:
vF=R⋅ωF
- And for the rear wheel:
vR=2R⋅ωR
3. Equate the Linear Speeds of the Centers of the Wheels:
- Since the bicycle is moving forward, the linear speeds of the centers of both wheels must be the same:
vF=vR
4. Express the Speeds in Terms of Angular Speeds:
- From the equations for vF and vR:
R⋅ωF=2R⋅ωR
5. Simplify the Equation:
- Dividing both sides by R (assuming R≠0):
ωF=2⋅ωR
- This shows that the angular speed of the front wheel is twice that of the rear wheel.
6. Determine the Speeds of the Topmost Points:
- The speed of the topmost point of the front wheel vtop,F is:
vtop,F=vF+R⋅ωF
- The speed of the topmost point of the rear wheel vtop,R is:
vtop,R=vR+2R⋅ωR
- Since vF=vR, we can substitute vF for vR:
vtop,F=vF+R⋅(2⋅ωR)=vF+2R⋅ωR
- Therefore, we find that:
vtop,F=vF+vR=2vR
- This means:
vtop,F=vtop,R
7. Conclusion:
- The speeds of the topmost points of both wheels are equal, hence:
vF=vR
Final Answer:
Both vF and vR are equal at the topmost points of the front and rear wheels.
- Let the radius of the front wheel be R.
- Then, the radius of the rear wheel will be 2R (as given in the problem).
- The linear speed v of a point on the circumference of a wheel is related to its angular speed ω and radius r by the equation:
v=r⋅ω
- Thus, for the front wheel:
vF=R⋅ωF
- And for the rear wheel:
vR=2R⋅ωR
- Since the bicycle is moving forward, the linear speeds of the centers of both wheels must be the same:
vF=vR
- From the equations for vF and vR:
R⋅ωF=2R⋅ωR
- Dividing both sides by R (assuming R≠0):
ωF=2⋅ωR
- This shows that the angular speed of the front wheel is twice that of the rear wheel.
- The speed of the topmost point of the front wheel vtop,F is:
vtop,F=vF+R⋅ωF
- The speed of the topmost point of the rear wheel vtop,R is:
vtop,R=vR+2R⋅ωR
- Since vF=vR, we can substitute vF for vR:
vtop,F=vF+R⋅(2⋅ωR)=vF+2R⋅ωR
- Therefore, we find that:
vtop,F=vF+vR=2vR
- This means:
vtop,F=vtop,R
- The speeds of the topmost points of both wheels are equal, hence:
vF=vR
Both vF and vR are equal at the topmost points of the front and rear wheels.
Topper's Solved these Questions
Similar Questions
10 In a bicycle the radius of rear wheel is twice the radius of front wheel.If rF and rr are the radii,vF and vr are speeds of top most points of wheel,then
(A) vr=2vF" (B) vF=2vr (C) vF=vr (D) vF>vrView SolutionThe rear wheel on a clown's bicycle has twice the radius of the front wheel. (a) When the bicycle is moving, is the linear speed at the very top of the rear wheel greater than, less than, or the same as that of the very top of the front wheel? (b) Is the angular speed of the rear wheel greater than, less than, or the same as that of the front wheel?
View Solution
Knowledge Check
- Question 1 - Select One
In a bicycle the radius of rear wheel is twice the radius of front wheel. If vF and vr are the speeds of top most points of front and rear wheels respectively, then :
Av=2 vBv=2 vCv=vDv>v - Question 2 - Select One
In a bicycle the radius of rear wheel is twice the radius of front wheel. If vF and vr are the speeds of top most points of front and rear wheels respectively, then :
Avr=2vfBvf=2vrCvf=2vrDvf=vr - Question 3 - Select One
the radus if the rear wheel of bicycle is twice that of the front wheel. When the bicycle is moving . The angular speed of the rear wheel compared to that of the front is
AGreaterBsmallerCsameDexact double
A wheel is rolling uniformly along a level road (see figure). The speed of transitional motion of the wheel axis is V. What are the speeds of the points A and B on the wheel rim relative to the road at the instant shown in the figure?
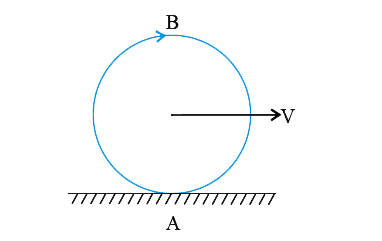 View Solution
View SolutionA bicycle moves on a horizontal road with some acceleration. The forces of friction between the road and the front and rear wheels are F1 and F2 respectively.
View SolutionA bicycle moves on a horizontal road with some acceleration. The forces of friction between the road and the front and rear wheels are F1 and F2 respectively.
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View SolutionA bicycle wheel makes 5000 revolutions in moving 11km. Then the radius of the wheel (in cm) is
View Solution

