In a diatiomic molecule, the rotational energy at a given temperature
obeys Maxwell's distribution
have the same value for all molecules
equals the translational kinetic energy for each molecule
is (2/3) rd the translational kinetic energy for each molecule
To solve the problem regarding the rotational energy of a diatomic molecule at a given temperature, we can follow these steps:
1. Understanding Degrees of Freedom:
- A diatomic molecule has translational and rotational degrees of freedom.
- For translational motion, a diatomic molecule has 3 degrees of freedom (movement along x, y, and z axes).
- For rotational motion, it has 2 degrees of freedom (rotation about two perpendicular axes perpendicular to the bond axis).
2. Translational Kinetic Energy:
- The translational kinetic energy (TKE) for a diatomic molecule can be expressed using the formula:
TKE=32kBT
- Here, kB is the Boltzmann constant and T is the temperature.
3. Rotational Kinetic Energy:
- The rotational kinetic energy (RKE) for a diatomic molecule can be expressed as:
RKE=22kBT=kBT
- This is because there are 2 degrees of freedom contributing to the rotational energy.
4. Relationship Between TKE and RKE:
- From the above equations, we can compare the translational and rotational kinetic energies:
TKERKE=32kBTkBT=32
- This implies that the translational kinetic energy is 32 times the rotational kinetic energy.
5. Conclusion:
- Therefore, we can conclude that the rotational energy of a diatomic molecule at a given temperature is:
RKE=23TKE
- This means that the rotational energy is two-thirds of the translational kinetic energy.
Final Answer:
The rotational energy of a diatomic molecule at a given temperature is two-thirds of its translational kinetic energy.
- A diatomic molecule has translational and rotational degrees of freedom.
- For translational motion, a diatomic molecule has 3 degrees of freedom (movement along x, y, and z axes).
- For rotational motion, it has 2 degrees of freedom (rotation about two perpendicular axes perpendicular to the bond axis).
- The translational kinetic energy (TKE) for a diatomic molecule can be expressed using the formula:
TKE=32kBT
- Here, kB is the Boltzmann constant and T is the temperature.
- The rotational kinetic energy (RKE) for a diatomic molecule can be expressed as:
RKE=22kBT=kBT
- This is because there are 2 degrees of freedom contributing to the rotational energy.
- From the above equations, we can compare the translational and rotational kinetic energies:
TKERKE=32kBTkBT=32
- This implies that the translational kinetic energy is 32 times the rotational kinetic energy.
- Therefore, we can conclude that the rotational energy of a diatomic molecule at a given temperature is:
RKE=23TKE
- This means that the rotational energy is two-thirds of the translational kinetic energy.
The rotational energy of a diatomic molecule at a given temperature is two-thirds of its translational kinetic energy.
Topper's Solved these Questions
Similar Questions
According to the law of equipartition of energy, internal energy of an ideal gas at a given temperature, is equally distributed in translational and rotational kinetic energies.
Rotational kinetic energy of a monoatomic gas is zero.View SolutionWhich of the following paramenters is the same for molecules of all gases at a given temperature?
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
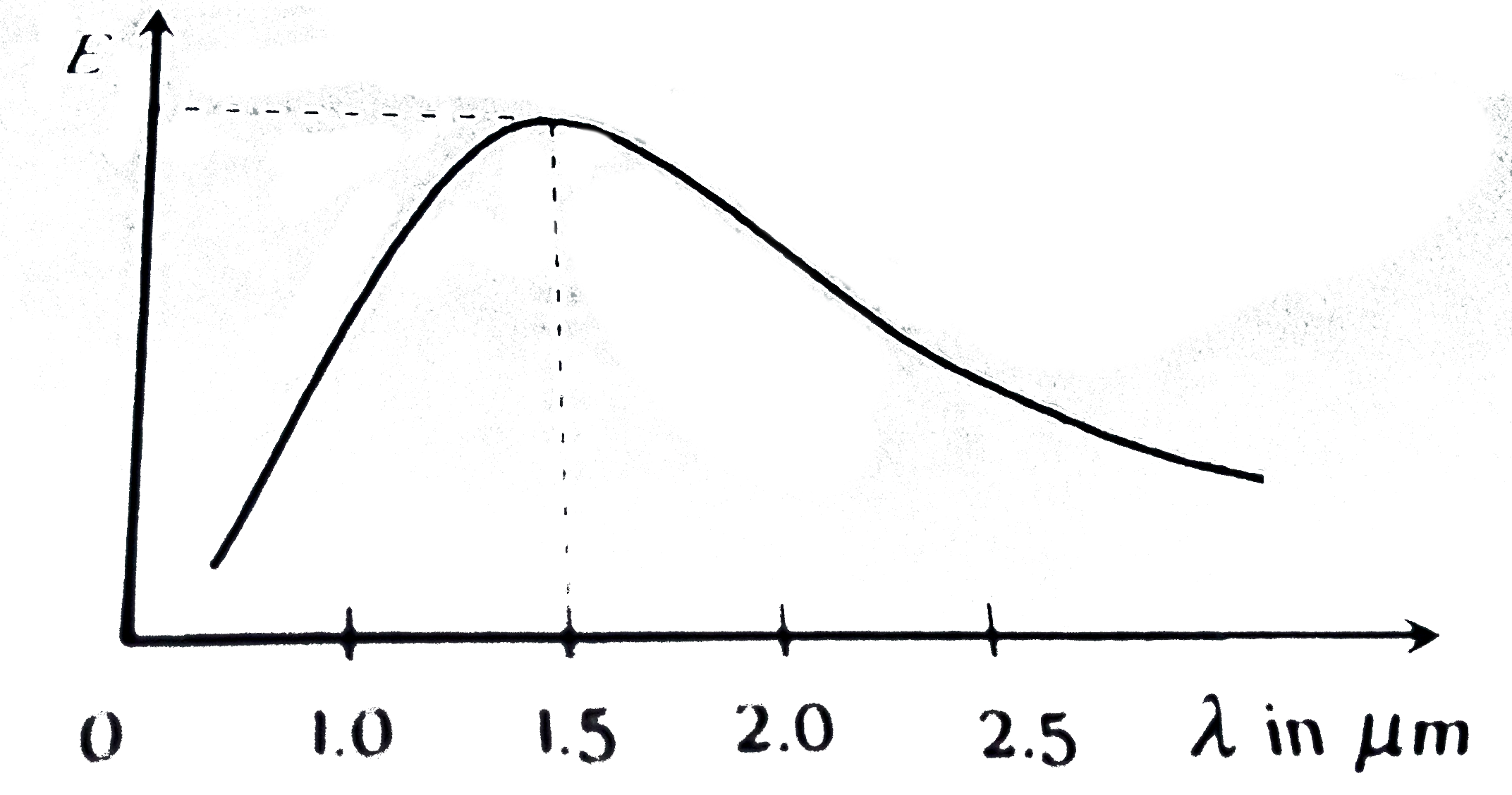 View Solution
View SolutionAssertion Total internal energy of oxygen gas at a given temperature is E of this energy 35 E is rotational kinetic energy.
Reason Potantial energy of an ideal gas is zero.View SolutionThe translational kinetic energy of one mole oxygen gas at a temperature is 15x10−20J. Its rotational kinetic energy at same temperature is
View SolutionThe ratio of translational and rotational kinetic energies at 100K temperature is 3:2. Then the internal energy of one mole gas at that temperature is (R=8.3j/mol−K]
View SolutionStatement-1. Most probable velocity is the velocity possesed by the maximum fraction of the molecules at a given temperature.
Statement-2. On collision, more and more molecules acquire higher speed at the same temperature.View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperatureView SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperatureView SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures, they may also have vibrational energy. As a result of this, at higher temperatures, molar specific heat capacity at constant volume, CV is
View Solution

