Diatomic molecules like hydrogen have energies due to both translations as well as rotational motion. From the equation in kinetic theory pV=23E,E is
The total energy per unit volume
only the translational part of energy because rotational energy is very small compared to the translational energy.
only the translational part of the energy because during collisions with the wall pressure relates to change in linear momentum
the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero
According to kinetic theory we assume the walls only exert perpendicular forces on molecules. They do not exert any parallel force, hence there will not be any type of rotation present.
The wall producess only change in translational motion.
Hence , in the equation
pV=23E [wherep= pressureV=volume]
E is representing only translational part of energy.
Topper's Solved these Questions
Similar Questions
For a diatomic gas having 3 translational and 2 rotational degree of freedom ,the energy is given by ?
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
In a CO molecule, the distance between C(mass=12a.m.u)andO(mass=16a.m.u) where 1a.m.u=53×10−27kg,is close to
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
In a CO molecule, the distance between C(mass=12a.m.u)andO(mass=16a.m.u) where 1a.m.u=53×10−27kg,is close to
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperature
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperature
View SolutionRotational energy levels of diatomic molecules are well described by the formula EJ=BJ(J+1), where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced
mass μ and the bond length R of the molecule through the equation B=h28π2μR2.
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=ΔE). The observed rotational transitions occur between adjacent rotational levels, hence ΔE=EJ+1−EJ=2B(J+1). Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Δυ)=2B.
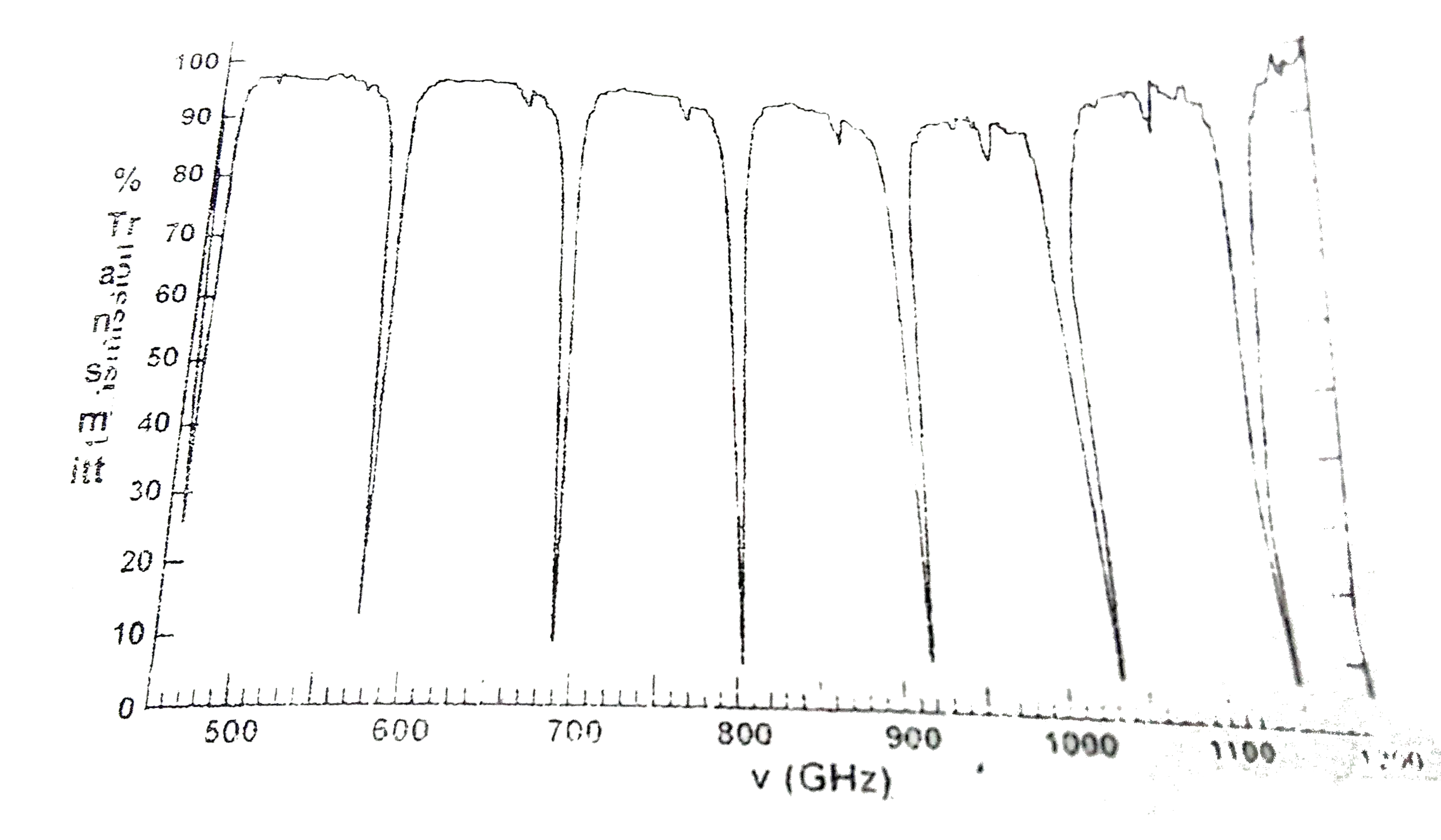
By inspecting the spectrum provided, determine the following quantities for ^(2)CpC with appropriate units
(a) Δυ (b) B (c) R
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures, they may also have vibrational energy. As a result of this, at higher temperatures, molar specific heat capacity at constant volume, CV is
View SolutionCalculate the dimensional formula of energy from the equation E=12mv2.
View SolutionA vessel contains a mixture of 2 moles o hydrogen and 3 moles of oxygen at a constant temperature. The ratio of average translational kinetic energy per H2 molecule to that per O2 molecule is
View SolutionThe total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are EKx,EKy,EKz
Total K.e =EKx+EKy+EKz
Since the motion of molecule is equally probable in all the three directions, therefore
EKx=EKy=EKz=13EK=13×32kT=12kT, where k=RNA = Botzman constant.
K.E.=12kT per molecule or =12RT per mole.
In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom.
Vibration energy =2×12kT=2×12RT [∴ two degrees of freedom per mole]
If the gas molecules have n1 translational degrees of freedom, n2 rotational degrees of freedom and n3 vibrational degrees of freedom, that total energy = n1[kT2]+n2[kT2]+n3[kT2]×2

Where 'n' is atomicity of gas.
The rotational kinetic energy of H20 molecule is equal to
View Solution
