In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.

c.m form m1
rc.m.=m2dm1+m2,d−rc.m.=m1dm1+m2
Gm1m2d2=m1rc.m.ω2
=m1m2dm1+m2ω2
ω2=G(m1+m2)d3
T=2πω=2πd3/2√G(m1+m2)
L1L2=I1ωI2ω=m1r2c.m.m2(d−rc.m.)2=m1m2(m2m1)2=m2m1
K1K2=12I1ω212I2ω2=m2m1
Topper's Solved these Questions
Similar Questions
In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of eavolution.
(b) the ratio of rheir kintic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.View SolutionIn a double star, two stars (one of mass m and the other of mass 2m) distance d apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.
View Solution
Knowledge Check
- Question 1 - Select One
In a double star system one of mass m1 and another of mass m2 with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass m1 to star of mass m2 about their common centre of mass is
Am1m2Bm2m1Cm21m22Dm22m21 - Question 2 - Select One
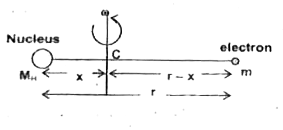
The angular momentum of the atom about the centre of mass will beAmr2ωBm(r−X)2ωC(MH+M)r2ωMHm2DMHmMH+mr2ω - Question 3 - Select One
Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
A12π√d33GmB2π√d33GmC12π√3Gmd3D2π√3Gmd3
In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.View SolutionIn a double star system, two stars of masses m1 and m2 separated by a distance x rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View SolutionTwo bodies of masses m1 and m2 have equal kinetic energies. What is the ratio of their linear momenta?
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionTwo bodies of masses M and 4M are moving with equal kinetic energy. The ratio of their linear momenta is
View Solution

