In a meter bridge experiment null point is obtained at 20 cm. from one end of the wire when resistance X is balanced against another resistance Y. If XltY, then where will be the new position of the null point from the same end, if one deicdes to balance a resistance of 4 X against Y
40 cm
80 cm
50 cm
70 cm
The correct Answer is:C
To solve the problem, we will use the principles of the meter bridge experiment. The meter bridge is based on the principle of Wheatstone bridge, where the ratio of the resistances is equal to the ratio of the lengths of the wire.
1. Understanding the Initial Setup:
- In the initial setup, we have a meter bridge with a null point obtained at 20 cm from one end when resistance X is balanced against resistance Y.
- This means that the length of wire corresponding to resistance X is 20 cm, and the length corresponding to resistance Y is 100−20=80 cm.
2. Using the Balance Condition:
- According to the meter bridge principle, we have:
XY=L100−L
- Substituting the known lengths:
XY=2080=14
- This implies that Y=4X.
3. Setting Up for New Resistance:
- Now, we want to balance a resistance of 4X against Y.
- We need to find the new null point L when balancing 4X against Y.
4. Applying the Balance Condition Again:
- Using the same principle:
4XY=L100−L
- Since we know from the previous calculation that Y=4X, we can substitute Y into the equation:
4X4X=L100−L
- This simplifies to:
1=L100−L
5. Solving for L:
- Cross-multiplying gives:
100−L=L
- Rearranging this equation:
100=2L⟹L=50 cm
6. Conclusion:
- The new position of the null point when balancing a resistance of 4X against Y will be at 50 cm from the same end of the wire.
Final Answer:
The new position of the null point is at 50 cm from the same end.
- In the initial setup, we have a meter bridge with a null point obtained at 20 cm from one end when resistance X is balanced against resistance Y.
- This means that the length of wire corresponding to resistance X is 20 cm, and the length corresponding to resistance Y is 100−20=80 cm.
- According to the meter bridge principle, we have:
XY=L100−L
- Substituting the known lengths:
XY=2080=14
- This implies that Y=4X.
- Now, we want to balance a resistance of 4X against Y.
- We need to find the new null point L when balancing 4X against Y.
- Using the same principle:
4XY=L100−L
- Since we know from the previous calculation that Y=4X, we can substitute Y into the equation:
4X4X=L100−L
- This simplifies to:
1=L100−L
- Cross-multiplying gives:
100−L=L
- Rearranging this equation:
100=2L⟹L=50 cm
- The new position of the null point when balancing a resistance of 4X against Y will be at 50 cm from the same end of the wire.
The new position of the null point is at 50 cm from the same end.
Topper's Solved these Questions
Similar Questions
In a meter bridge experiment shown below, the null point is obtained at P. The value of unknown resistance X is 2012 50 cm 1.) E
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View Solution
Knowledge Check
In a meter bridge experiment, the null point is obtained at 20cmfrom one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then where will be the new position of the null point from the same end, if one decides to balanced a resistance of 4X against Y?
A50 cmB80 cmC40 cmD70 cmIn a meter bridge experiment, the null point is obtained at 20cmfrom one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then where will be the new position of the null point from the same end, if one decides to balanced a resistance of 4X against Y?
A50cmB80cmC40cmD70cmIn a meter bridge experiment, null point is obtained at 20 cm &om one end of the wire when resistance X is balanced against another resistance Y". If X < y, then where will be the new position of the null point from the same end if one decides to, balance a resistance of 4X against Y?
A50 cmB80 cmC40 cmD70 cm
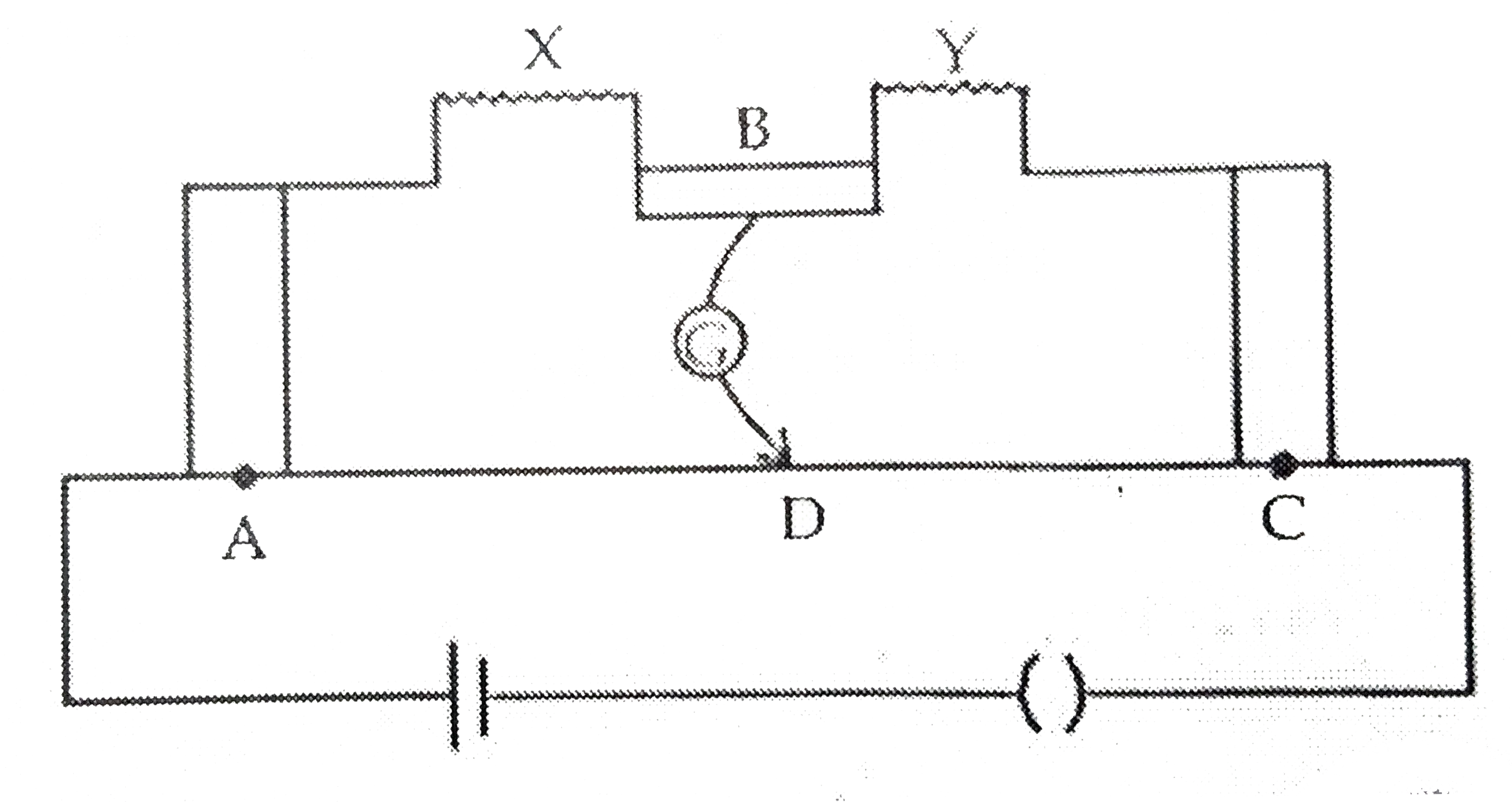
The figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View SolutionIn a meter bridge the null point is obtained at the middle point of the wire. If in one gap the resistance is 10Ω, then the value of resistance in the other gap is :–
View SolutionIn an experiment of meter bridge, a null point is obtaining at the center of the bridge wire. When a resistance of 10ohm is connected in one gap, the value of resistance other gap is
View Solution
