Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources are R1andR2(R1>R1). if the potential difference across the source having internal resistance R2 is zero, then
R=R2−R1
R=R2×(R1+R2)/(R2−R1)
R=R1R2/(R2−R1)
R=R1R2/(R1−R2)
The correct Answer is:A
To solve the problem step by step, we need to analyze the circuit with two sources of equal EMF connected to an external resistance R and internal resistances R1 and R2. Given that the potential difference across the source with internal resistance R2 is zero, we can derive the required relationship.
1. Understanding the Circuit Configuration:
- We have two sources of equal EMF V.
- The internal resistances are R1 and R2 respectively, with the condition R1>R2.
- The external resistance is R.
2. Setting Up the Circuit:
- Let’s denote the current flowing through the circuit as I.
- The total EMF in the circuit is 2V (since both sources contribute equally).
- The total internal resistance in the circuit is R1+R2.
3. Calculating the Current:
- The equivalent resistance Req of the circuit is given by:
Req=R+R1+R2
- The current I flowing through the circuit can be expressed as:
I=2VR+R1+R2
4. Analyzing the Potential Difference Across R2:
- The potential difference across the source with internal resistance R2 is given as zero. This means:
VA−VB=0
- Where VA is the potential at the positive terminal of the source with R2 and VB is the potential at the negative terminal.
- Using Ohm's law, we can express this as:
VA−V+I⋅R2=VB
- Since VA−VB=0, we have:
V−I⋅R2=0⇒V=I⋅R2
5. Substituting for Current I:
- Substitute the expression for I:
V=(2VR+R1+R2)R2
6. Simplifying the Equation:
- Cancel V from both sides (assuming V≠0):
1=2R2R+R1+R2
- Cross-multiplying gives:
R+R1+R2=2R2
- Rearranging this equation leads to:
R+R1=R2
7. Final Relationship:
- Thus, we find:
R=R2−R1
Conclusion:
The relationship derived from the conditions given in the problem is:
R=R2−R1
- We have two sources of equal EMF V.
- The internal resistances are R1 and R2 respectively, with the condition R1>R2.
- The external resistance is R.
- Let’s denote the current flowing through the circuit as I.
- The total EMF in the circuit is 2V (since both sources contribute equally).
- The total internal resistance in the circuit is R1+R2.
- The equivalent resistance Req of the circuit is given by:
Req=R+R1+R2
- The current I flowing through the circuit can be expressed as:
I=2VR+R1+R2
- The potential difference across the source with internal resistance R2 is given as zero. This means:
VA−VB=0
- Where VA is the potential at the positive terminal of the source with R2 and VB is the potential at the negative terminal.
- Using Ohm's law, we can express this as:
VA−V+I⋅R2=VB
- Since VA−VB=0, we have:
V−I⋅R2=0⇒V=I⋅R2
- Substitute the expression for I:
V=(2VR+R1+R2)R2
- Cancel V from both sides (assuming V≠0):
1=2R2R+R1+R2
- Cross-multiplying gives:
R+R1+R2=2R2
- Rearranging this equation leads to:
R+R1=R2
- Thus, we find:
R=R2−R1
The relationship derived from the conditions given in the problem is:
R=R2−R1
Topper's Solved these Questions
Similar Questions
Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
View SolutionTwo sources of current of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View Solution
Knowledge Check
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
AR1−R2BR1+R22CR1−R22DR1+R2Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
Ar1−r2Br1+r22Cr1−r22Dr1+r2Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
Ar1−r2Br1+r22Cr1−r22Dr1+r2
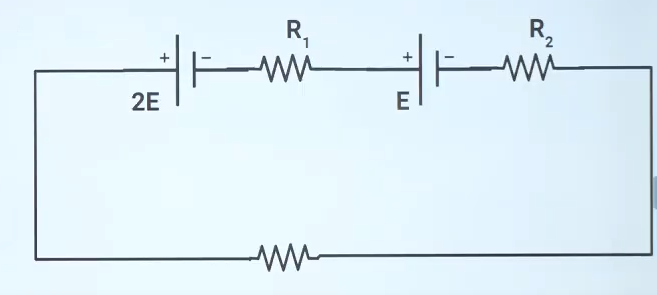
Internal resistance of battery of emf 2E is R1 and battery of emf E is R2. If the potential difference across the cell of emf 2E is zero, then value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionCell having an emfε internal resistance r is connected a variable external resistance R As the resistance R is increased the piot of potential difference V across R is given by
View Solution
