In a Michelson experiment for measuring speed of light, the distance travelled by light between two reflections from the rotating mirror is 4.8 km. The rotating mirror has a shape of a regular octagon. At what minimum angular speed of the mirror (other than zero) the image is formed at the position where a non rotating mirror forms it ?
The correct Answer is:A, C
To solve the problem of finding the minimum angular speed of the rotating mirror in a Michelson experiment, we can follow these steps:
1. Understand the Problem:
We need to determine the minimum angular speed (ω) of a rotating octagonal mirror such that the image formed is at the same position as it would be with a non-rotating mirror.
2. Identify Given Values:
- Distance travelled by light between two reflections (d) = 4.8 km = 4.8 × 10^3 m
- The number of sides of the octagonal mirror (n) = 8
- Speed of light (c) = 3 × 10^8 m/s
3. Use the Formula:
The formula to relate the angular speed of the mirror to the speed of light and the distance is:
ω=2πcd⋅n
This formula gives us the angular speed in radians per second.
4. Substitute the Values:
Substitute the known values into the formula:
ω=2π(3×108)(4.8×103)⋅8
5. Calculate the Denominator:
First, calculate the denominator:
d⋅n=(4.8×103)⋅8=3.84×104
6. Calculate ω:
Now substitute this back into the equation for ω:
ω=2π(3×108)3.84×104
Calculate the value:
ω=6.2832×3×1083.84×104≈7.8×103 radians/second
7. Convert to Revolutions per Second:
To convert from radians per second to revolutions per second, use the conversion factor 1 revolution2π radians:
Revolutions per second=7.8×1032π≈1.24×103 revolutions/second
8. Final Answer:
The minimum angular speed of the mirror is approximately:
ω≈7.8×103 radians/secondor1.24×103 revolutions/second
We need to determine the minimum angular speed (ω) of a rotating octagonal mirror such that the image formed is at the same position as it would be with a non-rotating mirror.
- Distance travelled by light between two reflections (d) = 4.8 km = 4.8 × 10^3 m
- The number of sides of the octagonal mirror (n) = 8
- Speed of light (c) = 3 × 10^8 m/s
The formula to relate the angular speed of the mirror to the speed of light and the distance is:
ω=2πcd⋅n
This formula gives us the angular speed in radians per second.
Substitute the known values into the formula:
ω=2π(3×108)(4.8×103)⋅8
First, calculate the denominator:
d⋅n=(4.8×103)⋅8=3.84×104
Now substitute this back into the equation for ω:
ω=2π(3×108)3.84×104
Calculate the value:
ω=6.2832×3×1083.84×104≈7.8×103 radians/second
To convert from radians per second to revolutions per second, use the conversion factor 1 revolution2π radians:
Revolutions per second=7.8×1032π≈1.24×103 revolutions/second
The minimum angular speed of the mirror is approximately:
ω≈7.8×103 radians/secondor1.24×103 revolutions/second
Topper's Solved these Questions
- SPEED OF LIGHTBOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Question for short Answer
5 Videos
- SPEED OF LIGHTBOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Objective -2
3 Videos
- SEMICONDUCTOR AND SEMICONDUCTOR DEVICESBOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer
11 Videos
- THE NUCLEOUSBOOK - HC VERMA ENGLISHCHAPTER - THE NUCLEOUSEXERCISE - Short answer
12 Videos
Similar Questions
In an experiment to measure the speed of light by Fizeau's apparatus, following data are used :
Distance between the mirrors = 12.0 km,
Number of teeth in the wheel = 180.
Find the minimum angular speed of the wheel for which the image is not seen.
View SolutionFor an object placed at a distance 20 cm from a concave mirror, the image is formed at the same position. What is the focal length of the mirror?
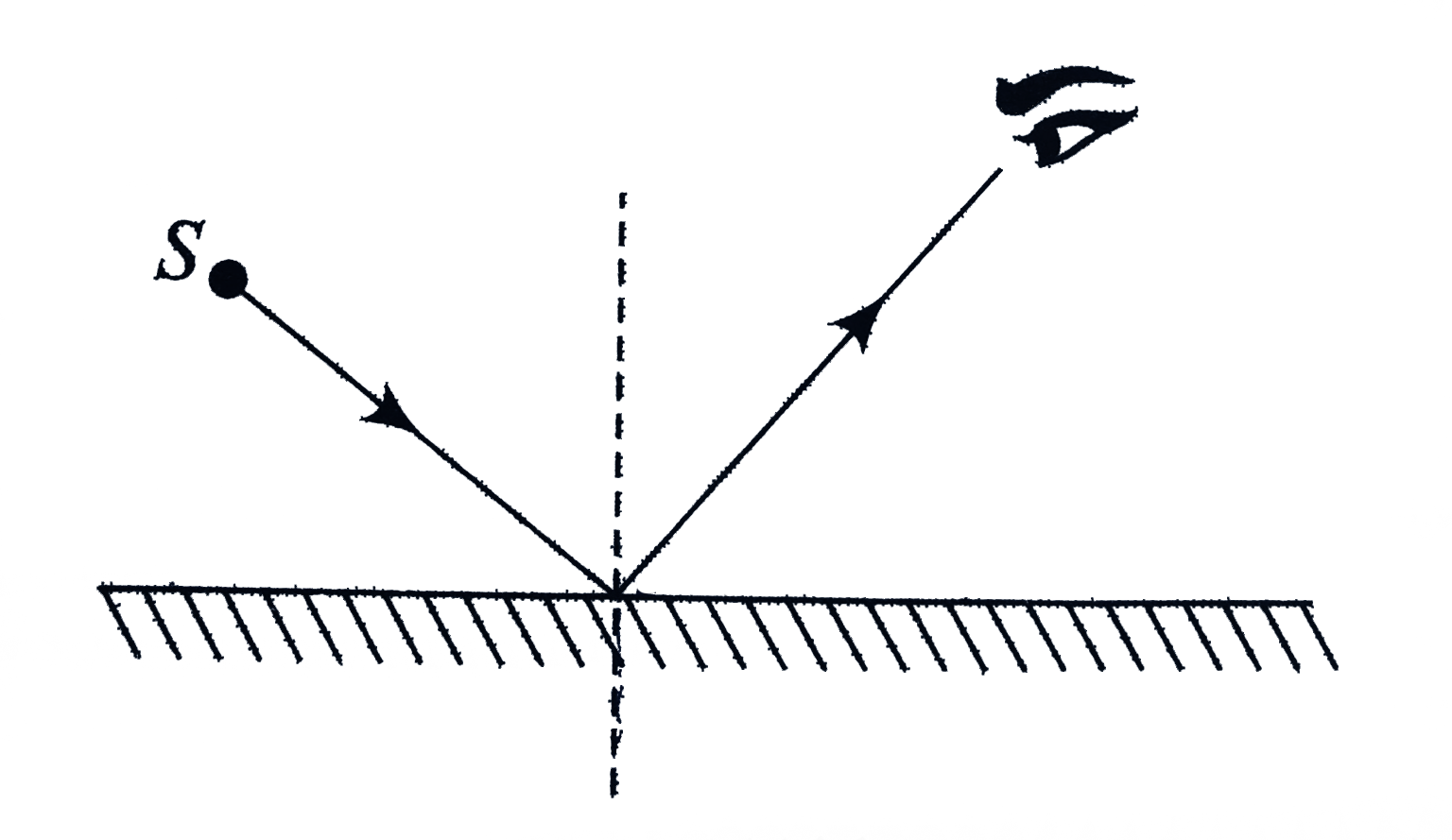
View SolutionA ray of light travels from a light source S to an observer after reflection from a plane mirror. If the source rotates in the clockwise direction by 10∘, by what angle and is what direction must the mirror be rotated so that the light ray still strikes the observer?
View SolutionA bird is flying with a velocity v between two long vertical mirrors making an angle θ with mirror M1 as shown. Then what will be the relative velocity of approach between the images formed by the mirrors due to the 1st reflection in each of them
_E01_004_Q01.png)
View SolutionBehind a thin converging lens having both the surfaces of the same radius 10cm, a plane mirror has been placed. The image of an object at a distance of 40 cm from the lens is formed at the same position. What is the refractive index of the lens?

View SolutionIn an experiment with Foucault's apparatus, the various distances used are as follows :
Distance between the rotating and the fixed mirror = 16 m
Distance between the lens and the rotating mirror = 6 m,
Distance between the source and the lens = 2 m. When the mirror is rotated at a speed of 356 revolutions per second, the image shifts by 0.7 mm. Calculate the speed of light from these data.
View SolutionThere are two plane mirror with reflecting suface faciing each other.The mirrors are moving with speed v away form each other .A point object is placed between the mirrors.The velocity of the n-th image will be
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. Determine the angle between the two mirrors:
View SolutionA light ray is incident on a rotating mirror, which is rotating with angular speed 3rad/s as shown in figure. The speed of bright spot on the wall when θ=30∘

View SolutionA point object is kept between a plane mirror and a concave mirror facing each other. The distance between the mirrors is 22.5 cm . The distance between the mirrors is 20 cm. what should be the distance of the object from the concave mirror so that after two successive reflections the final image is formed on the object itself ? (consider first reflection from concave mirror).
View Solution
