In a modified YDSE, monochromatic uniform and parallel beam of light of wavelength 6000A∘ and intensity (10π)W/m2 is incident normally on two circular apertures A and B of radii 1 mm and 2 mm respectively. Find the ratio of the intensity of the sources [IBIA] ?
The correct Answer is:4
To solve the problem of finding the ratio of the intensities of the sources IBIA in a modified Young's double slit experiment (YDSE) with two circular apertures, we can follow these steps:
Step 1: Understand the relationship between intensity and area
Intensity I is defined as the power per unit area. For circular apertures, the area can be calculated using the formula:
Area=πr2
where r is the radius of the aperture.
Step 2: Calculate the areas of the apertures
Given:
- Radius of aperture A, rA=1mm=0.001m
- Radius of aperture B, rB=2mm=0.002m
Now, calculate the areas:
AA=π(rA)2=π(0.001)2=π×10−6m2
AB=π(rB)2=π(0.002)2=π×4×10−6m2
Step 3: Use the intensity formula
The intensity of light is given by:
I=PA
where P is the power and A is the area. Since the power is the same for both apertures, we can express the intensities as:
IA=PAAandIB=PAB
Step 4: Find the ratio of the intensities
Now, we can find the ratio IBIA:
IBIA=P/ABP/AA=AAAB
Substituting the areas calculated:
IBIA=π×10−6π×4×10−6=14
Conclusion
Thus, the ratio of the intensities of the sources is:
IBIA=14
Intensity I is defined as the power per unit area. For circular apertures, the area can be calculated using the formula:
Area=πr2
where r is the radius of the aperture.
Given:
- Radius of aperture A, rA=1mm=0.001m
- Radius of aperture B, rB=2mm=0.002m
AA=π(rA)2=π(0.001)2=π×10−6m2
AB=π(rB)2=π(0.002)2=π×4×10−6m2
The intensity of light is given by:
I=PA
where P is the power and A is the area. Since the power is the same for both apertures, we can express the intensities as:
IA=PAAandIB=PAB
Now, we can find the ratio IBIA:
IBIA=P/ABP/AA=AAAB
IBIA=π×10−6π×4×10−6=14
Thus, the ratio of the intensities of the sources is:
IBIA=14
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet Exercise - II (DIFFRACTION) (Level - I (Main) (Straight objective Type questions)
3 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet Exercise - II (DIFFRACTION)(Level - II ) (Straight objective Type questions)
1 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Linked Comprehension Type Questions
3 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
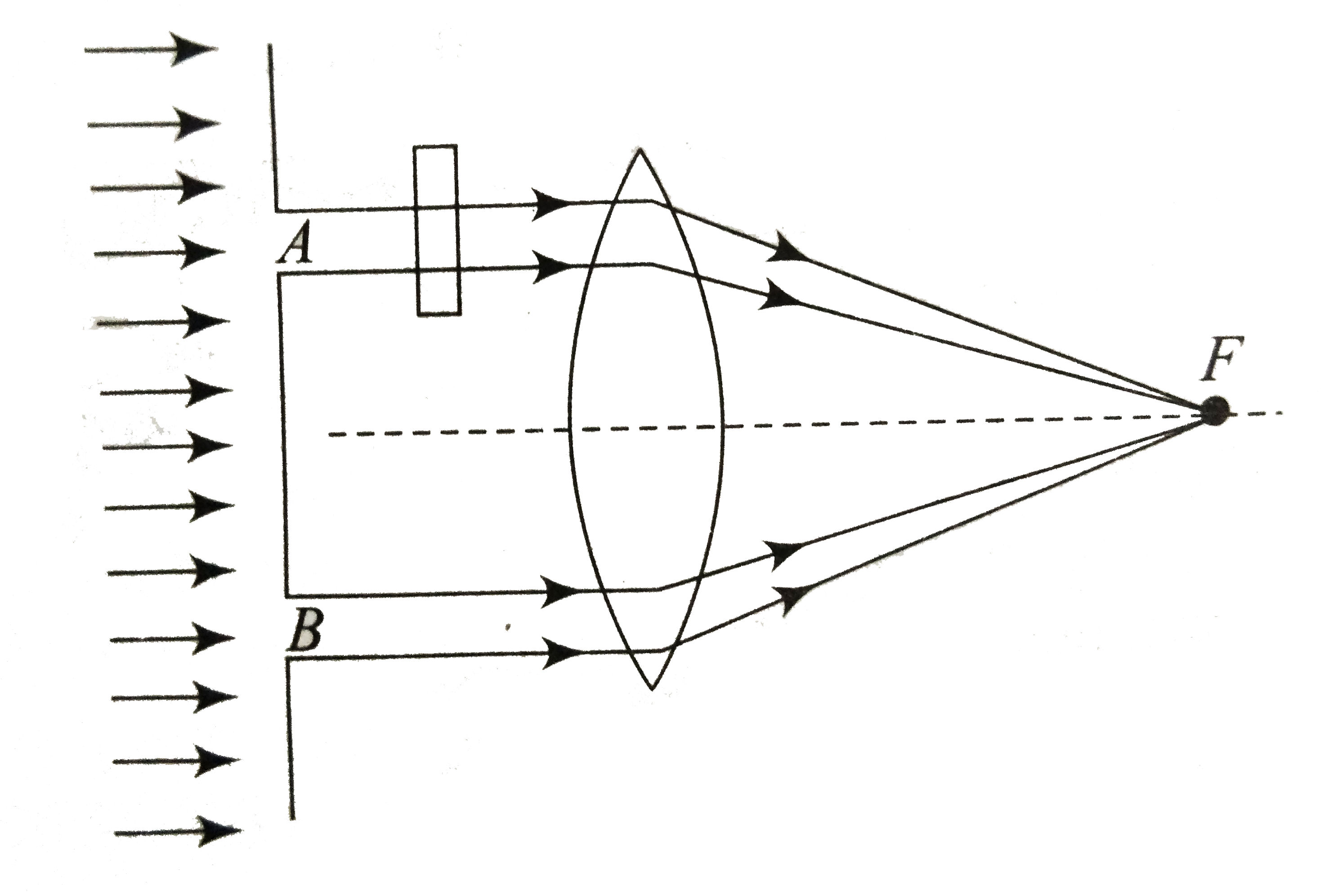
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
View SolutionConsider a parallel beam of light of wavelength 600nm and intensity 100W (m−2). (a) Find the energy and linear momentum of each photon. (b) How many photons cross 1 cm2 area perpendicular to the beam in one second?
View SolutionA parallel beam of uniform, monochromatic light of wavelength 6600 Å has an intensity of 900Wm−2. The number of photons in 1mm2 of this radiation are 1×10X then find out value of X.
View SolutionFind the resistance of a hollow cylindrical conductor of length 1.0m and inner and outer radii 1.0mm and 2.0mm respectively. The resistivity of the material is 2.0×10−8(Ω)m.
View SolutionMonochromatic light of wavelength 3000Å is incident on a surface area 4cm2. If intensity of light is 150mW/m2 , then rate at which photons strike the target is
View Solution_E01_102_Q01.png)
In a YDSE a parallel beam of light of wavelength 6000Å is incident on slits at angle of incidence 30∘. A and B are two thin transparent films each of refractive index 1.5. thickness of A is 20.4μm. Light coming through A and B have intensities I and 4I resepctively on the screen. Intensity at point O which is symmetric relative to the slits is 3I. The central maxima is above O.
(i). what is the maximum thickness of B to do so.
Assuming thickness of B to be that found in part (i)
Answer the following parts.
(ii). Find fringe width, maximum intensity and minimum intensity on screen.
(iii). Distance of nearest minima from O
(iv) intensity at 5 cm on either side of O.
View SolutionIn the figure shown a converging lens and a diverging lens of focal lengths 20cm and -5cm respectively are separated by a distance such that a paralel beam of light of intensity 100 wa/m2 incident on the converging lens comes out as parallel beam from the diverging lens. Find the intensity of the outgoing beam in wa/m2
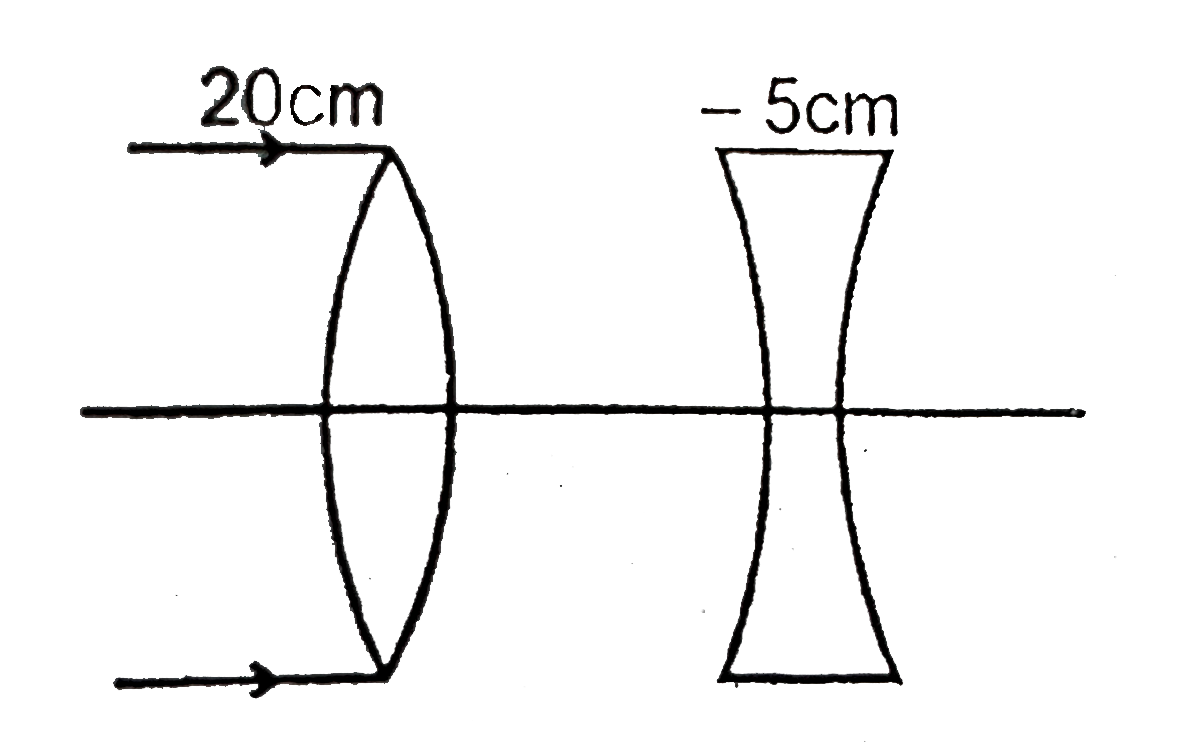
View SolutionLight of intensity 50W/m2 is incident on a arae of 1m2 in such a way that 25% of light is reflected back. Find the force exerted by light on surface if light incident perpendicularly
View SolutionTwo monochromatic ray of light are incident normally on the face AB of an isosceles right - angled 'I' and '2' are respectively 1.35 and 1.45. Trace path of these rays after entering through the prism.

View SolutionA parallel beam of monochromatic light of wavelength 500nm is incident normally on a perfectly absorbing surface. The power through any cross- section of the beam is 10 W. Find (a) the number of photons absorbed per second by the surface and (b) the force exerted by the light beam on the surface.
View Solution
