In a moving coil galvanometer the deflection (ϕ) on the scale by a pointer attached to the spring is
(NAkB)I
(NkAB)I
(NABk)I
(NABkI)
The correct Answer is:C
To solve the question regarding the deflection (Φ) on the scale by a pointer attached to the spring in a moving coil galvanometer, we can follow these steps:
1. Understand the Concept of Torque in a Galvanometer:
In a moving coil galvanometer, the coil experiences a torque when a current passes through it. The torque (τ) acting on the coil in a magnetic field is given by the formula:
τ=N⋅I⋅A⋅B
where:
- N = number of turns in the coil
- I = current through the coil
- A = area of the coil
- B = magnetic field strength
2. Counter Torque:
The coil also experiences a counter torque due to the spring attached to it, which opposes the movement of the coil. This counter torque can be expressed as:
τcounter=k⋅ϕ
where:
- k = torsional constant of the spring
- ϕ = deflection angle of the coil
3. Setting Up the Equation:
At equilibrium, the magnetic torque is balanced by the counter torque:
N⋅I⋅A⋅B=k⋅ϕ
4. Solving for Deflection (Φ):
Rearranging the equation to solve for ϕ:
ϕ=N⋅A⋅Bk⋅I
This equation shows that the deflection ϕ is directly proportional to the current I flowing through the coil.
5. Conclusion:
Therefore, the deflection ϕ on the scale by the pointer attached to the spring in a moving coil galvanometer is given by:
ϕ=N⋅A⋅Bk⋅I
In a moving coil galvanometer, the coil experiences a torque when a current passes through it. The torque (τ) acting on the coil in a magnetic field is given by the formula:
τ=N⋅I⋅A⋅B
where:
- N = number of turns in the coil
- I = current through the coil
- A = area of the coil
- B = magnetic field strength
The coil also experiences a counter torque due to the spring attached to it, which opposes the movement of the coil. This counter torque can be expressed as:
τcounter=k⋅ϕ
where:
- k = torsional constant of the spring
- ϕ = deflection angle of the coil
At equilibrium, the magnetic torque is balanced by the counter torque:
N⋅I⋅A⋅B=k⋅ϕ
Rearranging the equation to solve for ϕ:
ϕ=N⋅A⋅Bk⋅I
This equation shows that the deflection ϕ is directly proportional to the current I flowing through the coil.
Therefore, the deflection ϕ on the scale by the pointer attached to the spring in a moving coil galvanometer is given by:
ϕ=N⋅A⋅Bk⋅I
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
The conversion of a moving coil galvanometer into a voltmeter is done by
Aintroducing a resistance of large value in seriesBintroducing a resistance of small value in parallelCintroducing a resistance of large value in parallelDintroducing a resistance of small value in series
If in a moving coil galvanometer, a current I produces a deflection θ, then
View SolutionA moving coil galvanometer can be converted into a voltmeter by connecting :
View SolutionIn a hot wire ammeter the deflection angle θ of the pointer is related with the current I as
View SolutionWhen 0.005A current flows through a moving coil galvanometer, it gives fullscale deflection. It is converted into a voltmeter to read 5 Volt, using an external resistance of 975Ω. The resistance of galvanometer in ohms is
View SolutionIn a moving coil galvanometer, we use a radial magnetic field so that the galvanometer scale is
View SolutionWhen primary coil P is moved towards secondary coil S, Fig. the galvanometer shows memetary deflection in the can be done to have larger deflection in the galvanometer with same battery ? State the related law ?
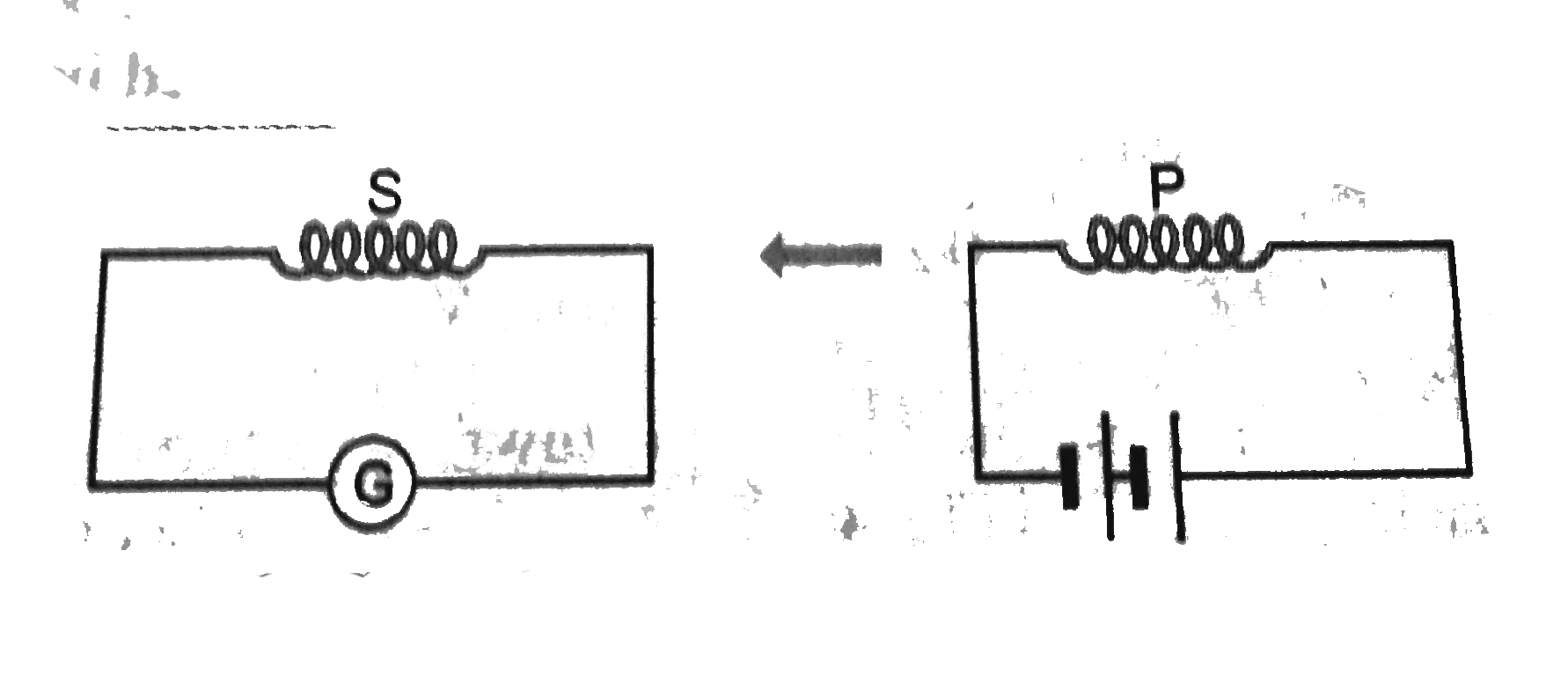 View Solution
View SolutionWhen a 12Ω resistor is connected with a moving coil galvanometer, then its deflection reduces form 50 divisions to 10 divisions. The ressitance of the galvanometer is
View Solution

