In a nuclear reactor, the fuel is consumed at the rate of 1mg/s. The power generated in kilowatt is
9×104
9×107
9×108
9×1012
The correct Answer is:B
To solve the problem of calculating the power generated in a nuclear reactor when the fuel is consumed at a rate of 1 mg/s, we can follow these steps:
Step 1: Understand the relationship between mass and energy
In nuclear reactions, the energy released when a mass m is converted to energy can be calculated using Einstein's mass-energy equivalence formula:
E=mc2
where c is the speed of light, approximately 3×108 m/s.
Step 2: Convert the mass consumption rate to kilograms
The fuel is consumed at a rate of 1 mg/s. To convert this to kilograms:
1 mg=1×10−3 g=1×10−6 kg
Thus, the mass consumption rate is:
mt=1×10−6 kg/s
Step 3: Calculate the energy generated per second
Using the mass-energy equivalence, the energy generated per second (which is power) can be calculated as:
P=Et=mtc2
Substituting the values:
P=(1×10−6 kg/s)×(3×108 m/s)2
Step 4: Calculate c2
Calculating c2:
c2=(3×108)2=9×1016 m2/s2
Step 5: Substitute c2 into the power equation
Now substituting c2 back into the power equation:
P=(1×10−6)×(9×1016)=9×1010 watts
Step 6: Convert watts to kilowatts
To convert watts to kilowatts, we divide by 1000:
P=9×10101000=9×107 kilowatts
Final Answer
The power generated in the nuclear reactor is:
9×107 kilowatts
---
In nuclear reactions, the energy released when a mass m is converted to energy can be calculated using Einstein's mass-energy equivalence formula:
E=mc2
where c is the speed of light, approximately 3×108 m/s.
The fuel is consumed at a rate of 1 mg/s. To convert this to kilograms:
1 mg=1×10−3 g=1×10−6 kg
Thus, the mass consumption rate is:
mt=1×10−6 kg/s
Using the mass-energy equivalence, the energy generated per second (which is power) can be calculated as:
P=Et=mtc2
Substituting the values:
P=(1×10−6 kg/s)×(3×108 m/s)2
Calculating c2:
c2=(3×108)2=9×1016 m2/s2
Now substituting c2 back into the power equation:
P=(1×10−6)×(9×1016)=9×1010 watts
To convert watts to kilowatts, we divide by 1000:
P=9×10101000=9×107 kilowatts
The power generated in the nuclear reactor is:
9×107 kilowatts
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Radioactivity42videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Radioactive Disintegration65videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - NUCLEAR PHYSICSEXERCISE - Section D - Chapter End Test29videos
NUCLEAR PHYSICS
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Mock Test 344videos
MOCK TEST
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
In given circuit determine .
(a) The rate at which chemical energy of the cell is consumed
(b) The rate at which heat is generated inside the battery
(c ) Electric power output
(d) Which resistance consumes maximum power
(e ) Power dissipated across 4Ω resistance
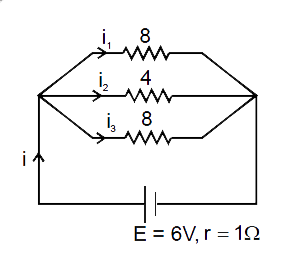 View Solution
View Solution(a) What is a nuclear reactor? What is the fuel used in a nuclear reactor?
(b) What type of nuclear reaction is carried out in a nuclear reactor?
(c ) How is the working nuclear reactor of a power plant shut down in an emergency?
(d) Name five places in India where nuclear power plants are located.View Solution
Knowledge Check
- Question 1 - Select One
The fuel used in the nuclear reactor is :
AGalliumBGermaniumCPotassiumDUranium - Question 2 - Select One
If the power of nuclear reactor is 100 watt then rate of nuclear fission is -
A3.6×106 per secondB3.2×1012 per secondC1.8×106 per secondD1.8×1012per second - Question 3 - Select One
In a certain nuclear reactor, a radioactive nucleus is bieng produced at a constant rate =1000/s The mean life of the radionuclide is 40 minutes. At steady state, the number of radionuclide will be
A4×104B24×104C24×105D24×106
(a) What is a nuclear reactor ? What is the fuel used in a nuclear reactor ?
(b) With the help of a labelled diagram, describe the working of a nuclear power plant.
(c ) How is the working nuclear reactor of a power plant shut down in an emergency ?
(d) Name five places in India where nuclear power plants are located.View SolutionIn a nuclear reactor ^235U undergoes fission liberating 200 MeV of energy. The reactor has a 10% efficiency and produces 1000 MW power. If the reactor is to function for 10 yr, find the total mass of uranium required.
View SolutionA nuclear reactor delivers a power of 10 W. Find fuel consumed by the reactor per hour, if its efficiency is 20%. (Given, c=3×108ms−1)
View SolutionReaction rate in a nuclear reactor is controlled through control rods. Controls rods reduces reaction rate by
View SolutionConsider the following statements:
1. Kudankulam has started generating electricity on a commercial basis after it received green signal from Nuclear Power Corporation (NPC).
2. Kudankulam Nuclear Power Plant is a nuclear power station in Koodankulam in Tamil Nadu with a capacity of generating 2000 MW with 2 reactors.
3. It is India’s largest nuclear reactor with the capacity of 1000 MV.
Which of the statements given above is/are correct?View Solution

