In a photocell the plates P and Q have a separation of 5 cm, which are connected through a galvanometer without any cell. Bichromatic light of wavelengths 4000Å and 6000Å are incidenton plate Q whose work- functionis 2.39 eV. If a uniform magnetic field B exists parallel to the plates, find the minimum value of B for which the galvanometer shows zero deflection.
The correct Answer is:A
To solve the problem step by step, we will follow the principles of the photoelectric effect and the motion of charged particles in a magnetic field.
Step 1: Calculate the energy of the incident photons
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- h=6.626×10−34Js (Planck's constant)
- c=3×108m/s (speed of light)
- λ is the wavelength in meters.
For the two wavelengths given:
1. For λ1=4000Å=4000×10−10m:
E1=(6.626×10−34)(3×108)4000×10−10≈3.1eV
2. For λ2=6000Å=6000×10−10m:
E2=(6.626×10−34)(3×108)6000×10−10≈2.06eV
Step 2: Determine if the photons can cause photoemission
The work function ϕ is given as 2.39eV. We compare the energies of the photons with the work function:
- E1=3.1eV>ϕ (photoemission occurs)
- E2=2.06eV<ϕ (no photoemission)
Only photons of wavelength 4000Å will cause photoemission.
Step 3: Calculate the kinetic energy of the emitted electrons
The kinetic energy K of the emitted electrons can be calculated as:
K=E1−ϕ=3.1eV−2.39eV=0.71eV
Step 4: Convert kinetic energy to joules
To work with SI units, we convert the kinetic energy from electron volts to joules:
K=0.71eV×1.6×10−19J/eV=1.136×10−19J
Step 5: Determine the radius of the semicircular path
The radius R of the semicircular path of the electrons in the magnetic field is given as R=0.05m (5 cm).
Step 6: Apply the formula for the radius of the path in a magnetic field
The radius of the path of a charged particle in a magnetic field is given by:
R=mvBq
where:
- m is the mass of the electron m=9.109×10−31kg
- v is the velocity of the electron
- B is the magnetic field strength
- q is the charge of the electron q=1.6×10−19C
Step 7: Relate kinetic energy to velocity
The kinetic energy is also related to the velocity as:
K=12mv2⟹v=√2Km
Substituting the value of K:
v=√2×1.136×10−199.109×10−31≈1.63×106m/s
Step 8: Substitute into the radius formula to find B
Rearranging the radius formula to solve for B:
B=mvRq
Substituting the values:
B=(9.109×10−31)(1.63×106)(0.05)(1.6×10−19)
Calculating:
B≈5.68×10−5T
Final Answer
The minimum value of the magnetic field B for which the galvanometer shows zero deflection is approximately:
B≈5.68×10−5T
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- h=6.626×10−34Js (Planck's constant)
- c=3×108m/s (speed of light)
- λ is the wavelength in meters.
1. For λ1=4000Å=4000×10−10m:
E1=(6.626×10−34)(3×108)4000×10−10≈3.1eV
2. For λ2=6000Å=6000×10−10m:
E2=(6.626×10−34)(3×108)6000×10−10≈2.06eV
The work function ϕ is given as 2.39eV. We compare the energies of the photons with the work function:
- E1=3.1eV>ϕ (photoemission occurs)
- E2=2.06eV<ϕ (no photoemission)
The kinetic energy K of the emitted electrons can be calculated as:
K=E1−ϕ=3.1eV−2.39eV=0.71eV
To work with SI units, we convert the kinetic energy from electron volts to joules:
K=0.71eV×1.6×10−19J/eV=1.136×10−19J
The radius R of the semicircular path of the electrons in the magnetic field is given as R=0.05m (5 cm).
The radius of the path of a charged particle in a magnetic field is given by:
R=mvBq
where:
- m is the mass of the electron m=9.109×10−31kg
- v is the velocity of the electron
- B is the magnetic field strength
- q is the charge of the electron q=1.6×10−19C
The kinetic energy is also related to the velocity as:
K=12mv2⟹v=√2Km
v=√2×1.136×10−199.109×10−31≈1.63×106m/s
Rearranging the radius formula to solve for B:
B=mvRq
B=(9.109×10−31)(1.63×106)(0.05)(1.6×10−19)
B≈5.68×10−5T
The minimum value of the magnetic field B for which the galvanometer shows zero deflection is approximately:
B≈5.68×10−5T
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.1
6 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.2
12 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 4
3 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
In a photocell bichromatic light of wavelength 2475Å and 6000Å are incident on cathode whose work function is 4.8eV. If a uniform magnetic field of 3×10−5Tesla exists parallel to the plate , the radius of the path describe by the photoelectron will be (mass of electron =9×10−31kg)
View SolutionIn an experiment on photoelectric effect, the emitter and the collector plates are placed at a separation of 10cm and are connected through an ammeter without any cell. A magnetic field B exists parallel to the plates. The work function of the emitter is 2.39 e V and the light incident on it has wavelengths between 400nm and 600nm. Find the minimum value of B for which the current registered by the ammeter is zero. Neglect any effect of space charge.

View SolutionLight of wavelength 180 nm ejects photoelectrons from a plate of metal whose work - function is 2 eV. If a uniform magnetic field of 5×10−5 T be applied parallel to the plate, what would be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
View SolutionA square coil of edge I having n turns carries a curent i. it is kept on a smooth horizontal plate. A uniform magnetic field B exists in a direction parallel to an edge the total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
View SolutionA square coil of edge I having n turns carries a curent i. it is kept on a smooth horizontal plate. A uniform magnetic field B exists in a direction parallel to an edge the total mass of the coil is M. What should be the minimum value of B for which the coil will start tipping over?
View SolutionTwo recangular plates A and B placed at a distance 2a apart, are connected to a battery to produce an electric field. There are insulators between plantes C and other two plates. A magnetic field exists along z-axis. A charged particle of mass m and charge q passes through a hole at the middle of the plate A with velocity v and strikes at Q which is the middle of the bottom edge of plate B after passing through a hole inplate C. If E=mv2/qa, what will be the speed of the particle at Q?
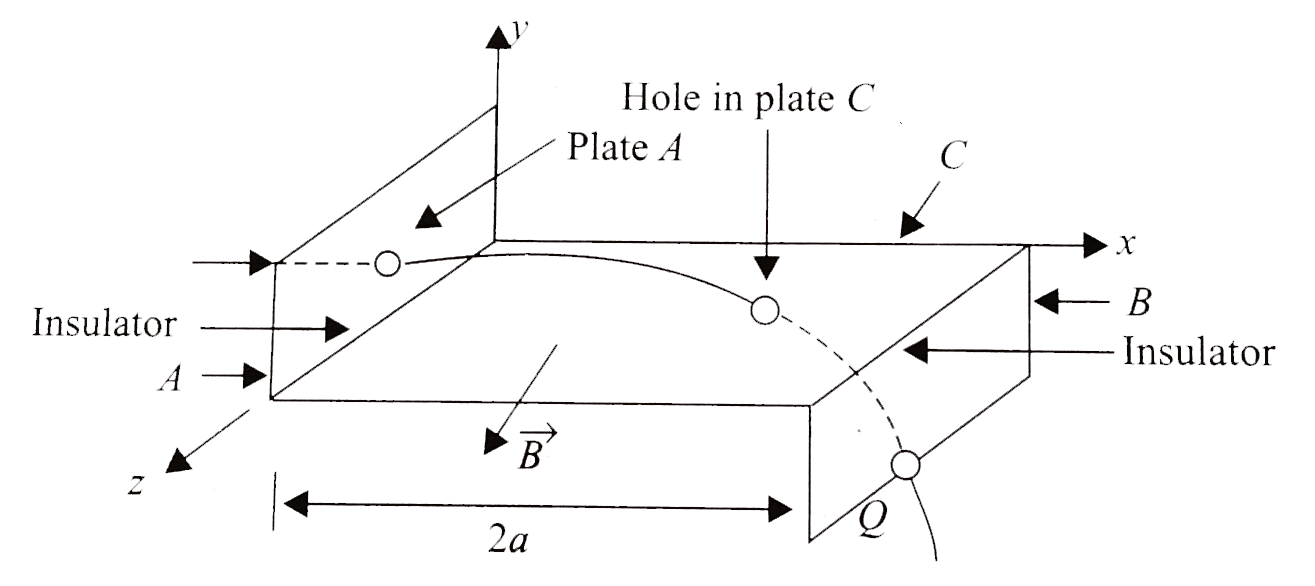
View Solution(a) The capacitors C1andC2 having plates of area A each are connected in series, as shown. Compare the capacitance of this combination with the capacitor C3, again having plates of area A each, but made up as shown in figure.
(b) The electric field inside a parallel plate capacitor is E. Find hte amount of work done in moving a charge q over a closed rectangular loop abcda.
View SolutionIn a moving coil galvanometer, torque on the coil can be experessed as τ=ki, where i is current through the wire and k is constant . The rectangular coil of the galvanometer having number of turns N , area A and moment of interia I is placed in magnetic field B. Find
(a) k in terms of given parameters N,I,AandB
(b) the torsion constant of the spring , if a current i0 produces a deflection of (π)/(2) in the coil .
(c) the maximum angle through which the coil is deflected, if charge Q is passed through the coil almost instaneously. ( ignore the daming in mechinal oscillations).
View SolutionIn a moving coil galvanometer, torque on the coil can be experessed as τ=ki, where i is current through the wire and k is constant . The rectangular coil of the galvanometer having number of turns N , area A and moment of interia I is placed in magnetic field B. Find
(a) k in terms of given parameters N,I,AandB
(b) the torsion constant of the spring , if a current i0 produces a deflection of (π)/(2) in the coil .
(c) the maximum angle through which the coil is deflected, if charge Q is passed through the coil almost instaneously. ( ignore the daming in mechinal oscillations).
View SolutionA parallel - plate capacitor having plate area 20cm2 and seperation between the plates 1.00mm is connected to a battery of 12.0V. The plates are pulled apart to increase the separation to 2.0mm . (a ) calculate the charge flown through the circuit during the process . (b ) How much energy is absorbed by the battery during the process ? (c ) calculate the stored energy in the electric field before and after the process . (d ) Using the expression for the force between the plates , find the work done by the person polling the plates apart . (e ) Show and justify that no heat is produced during this transfer of charge as the separation is increased.
View Solution
