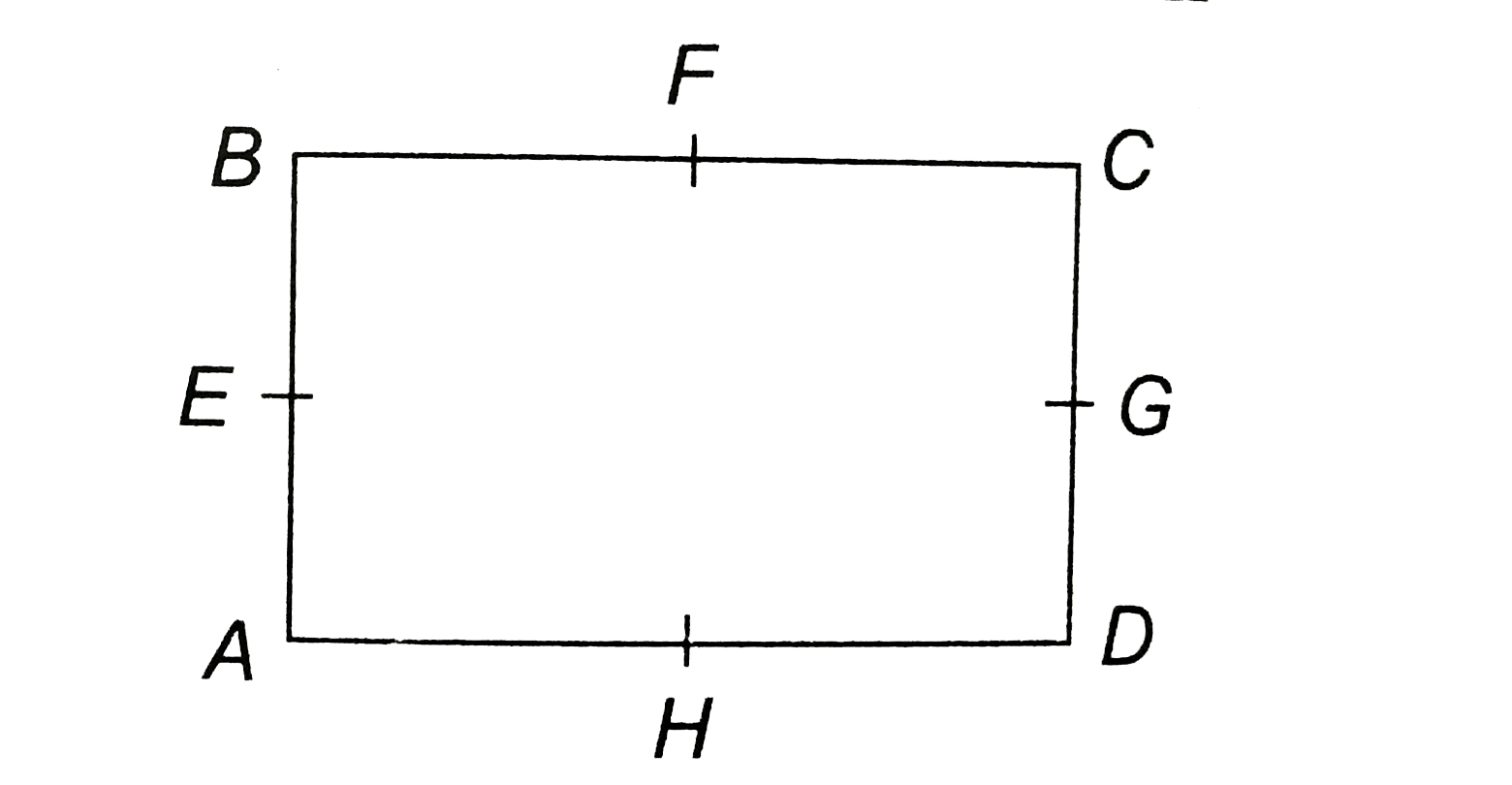
In a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
A
BC
B
BD
C
HF
D
EG
Video Solution
Text Solution
The moment of inertia will be minimum about that axis, which is passing through the center of mass.
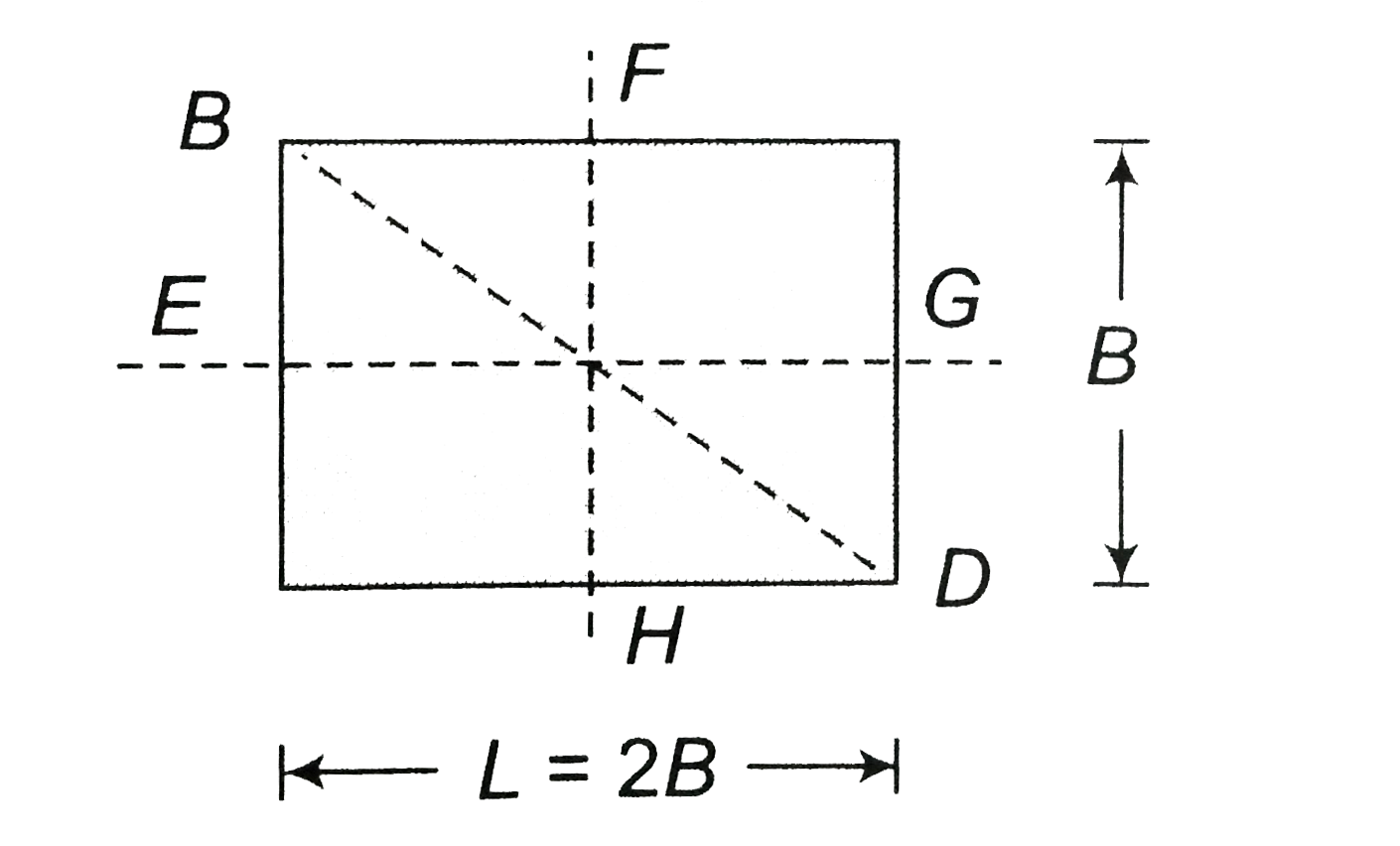
IEG=MB212
IFH=M(2B)212=MB26
M.I. of the rectangular plate about its diagonal
IBD=MB2L26(B2+L2)=MB2×4B26(B2+4B2)=215MB2=MB27.5
M.I. about EG is minimum.
OR
By observation, distribution of mass is the nearest about axis EG.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a rectangle ABCD (BC=2AB). The moment of inertia along which the axis will be minimum
 ABCBBDCHFDEG
ABCBBDCHFDEGIn a rectangle ABCD (BC=2AB). The moment of inertia along which axis will be minimum
 AEGBHFCBDDBC
AEGBHFCBDDBCIn a rectangle ABCD(BC=2AB). The moment of inertia is minimum along axis through
 ABCBBDCHFDEG
ABCBBDCHFDEG
In rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View SolutionABCD is a rectangle in which AB=10cms,BC=8cms.A point P is takes on AB such that PA=x Then the minimum value of PC2−PD2 is obtained when x=
View SolutionIn a rectangle ABCD(BC=2AB). The moment of inertia is maximum along axis through

View SolutionA wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
View SolutionMoment of inertia of a rod is minimum, when the axis passes through
View Solution