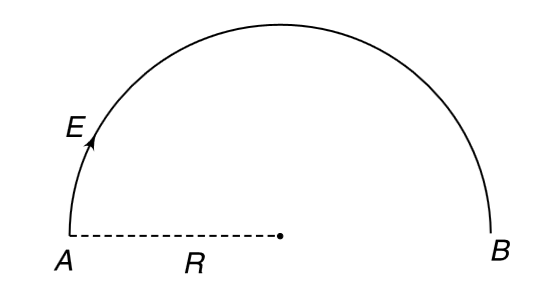
In a region of space an electric field line is in the shape of a semicircle of radius R. Magnitude of the field at all point is E. A particle of mass m having charge q is constrained to move along this field line. The particle is released from rest at A. (a) Find its kinetic energy when it reaches point B. (b) Find the acceleration of the particle when it is at midpoint of the path from A to B.
The correct Answer is:(a). KB=πqER
(b). at=qEm√1+π2
Step by step video, text & image solution for In a region of space an electric field line is in the shape of a semicircle of radius R. Magnitude of the field at all point is E. A particle of mass m having charge q is constrained to move along this field line. The particle is released from rest at A. (a) Find its kinetic energy when it reaches point B. (b) Find the acceleration of the particle when it is at midpoint of the path from A to B. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 2
77 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
A ball of mass m having a charge q is released from rest in a region where a horizontal electric field E exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.
View SolutionA particle of mass 'm' and charge 'Q' is acceleration in cyclotron. If magnetic field is 'B' and radius cyclotron is r then find the kinetic energy of particle.
View Solution
Knowledge Check
When a charged particle enters a uniform magnetic field its kinetic energy
Aremains constantBincreasedCdecreasesDbecomesWhen a charged particle enters a uniform magnetic field its kinetic energy
ARemains constantBIncreasesCDecreasesDBecomes zeroA charged particle is moved along a magnetic field line. The magnetic force on the particle is
Aalong its velocityBopposite to its velocityCperpendicular to its velocityDzero
A charged particle is moving along a magnetic field line. The magnetic force on the particle is
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA positively charged particle is released from rest in an uniform electric field. The electric potential energy of the charge
View Solution
