In a two block system in figure match the following.
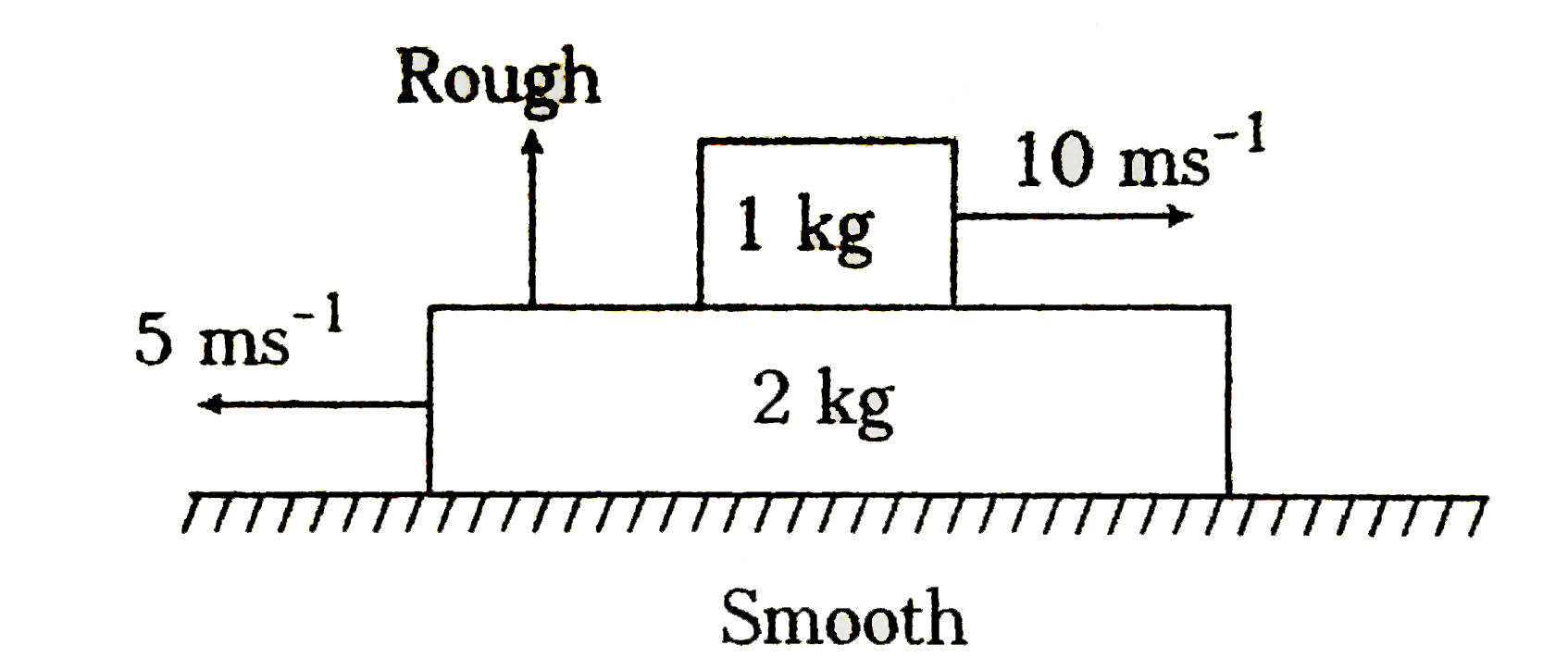 Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
The correct Answer is:A →r,s, B→r s, C→q, D→q
vCM = m1v−(1)+m2v−(2)m1+m−(2) = (1)(10)+(2)(−5)3 = 0<br>Similarly,p_(CM)=0
Net force on the system is zero, hence VCM and pCM will remain constant.
Velocity of 1 kg and 2kg blocks keep on changing initially and finally both of them stop as VCM was zero.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
In the arrangement shown in figure match the following
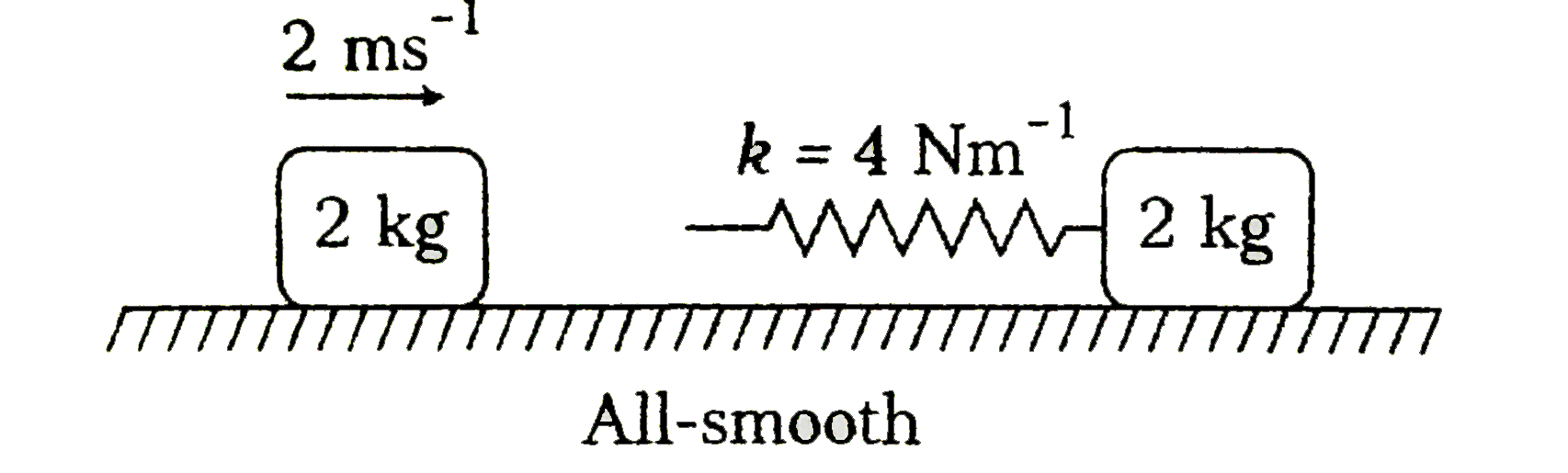
column1column2A Velocities of center of massP 2SI unitB Velocity of combined mass when compression in the spring is maximumQ 1 SI unitC Maximum compression in the springR 4 SIunitD Maximum potential energy stored in the springS 0.5SI unit
View SolutionFour point masses are placede at four corners of a square of side 4m as shown. Match the following columns.

Column1Column2A x-coordinate of center of mass of 4kg and 2kgP (7//2)mB x-coordinates of center of mass of 4kg 2kg and 3kgQ (4//3)mC y-coordinate of center of mass of 1kg 4kg and 3kgR 3my-coordinate of center of mass of 1kg and 3kg(20/9)m
View SolutionFour point masses are placede at four corners of a square of side 4m as shown. Match the following columns.

Column1Column2A x-coordinate of center of mass of 4kg and 2kgP (7//2)mB x-coordinates of center of mass of 4kg 2kg and 3kgQ (4//3)mC y-coordinate of center of mass of 1kg 4kg and 3kgR 3my-coordinate of center of mass of 1kg and 3kg(20/9)m
View SolutionIf net force on a system of particles is zero. Then
Column IColumn II(A)Acceleration of centre of mass(p)Constant(B)Velocity of centre of mass(q)Zero(C)Momentum of centre of mass(r)May be zero(D)Velocity of an individual particle of the system(s)May be constant
View SolutionIf net force on a system of particles is zero. Then
Column IColumn II(A)Acceleration of centre of mass(p)Constant(B)Velocity of centre of mass(q)Zero(C)Momentum of centre of mass(r)May br zero(D)Velocity of an individual particle of the system(s)May be constant
View SolutionIn the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unit
View SolutionIn the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unit
View SolutionIf radius if earth is reduced to half without changing its mass, then match the following columns
Column-IColumn-II(A)Angular momentum of earth(p)Will become two times(B)Time period of rotation of earth(q)Will become four times(C)Rotational kinetic energy of earth(r)Will remain constant(D)(s)None
View SolutionIf radius if earth is reduced to half without changing its mass, then match the following columns
Column-IColumn-II(A)Angular momentum of earth(p)Will become two times(B)Time period of rotation of earth(q)Will become four times(C)Rotational kinetic energy of earth(r)Will remain constant(D)(s)None
View SolutionMatch the appropriate Column I with Column II.
Column IColumn II(A) Same dimension of mass(P) electric charge(B) Negative dimension of mass(Q) electric potential(C) Zero dimension of mass(R) electric capacity(D) Dimension of length is±D(S) energy density
View Solution
