In a two dimensional steady flow the velocity of fluid particle at (x,y) is given by →V=(u0+bx)ˆi− by ˆj,u0 and b are positive constants. Write the equation of streamilnes. Draw few streamlines for x>0.
The correct Answer is:y=c0u0+bx where c0 is a constant. For plot of stremlines see the solution.
To find the equation of streamlines for the given velocity field in a two-dimensional steady flow, we start with the velocity vector provided:
→V=(u0+bx)^i−by^j
Here, u0 and b are positive constants. The components of the velocity vector are:
- u=u0+bx
- v=−by
Step 1: Understand the relationship between velocity and streamlines
The streamlines in a flow represent the paths that fluid particles follow. The slope of the streamline at any point is given by the ratio of the velocity components:
dydx=vu
Step 2: Substitute the velocity components
Substituting the expressions for u and v:
dydx=−byu0+bx
Step 3: Rearrange the equation
Rearranging gives:
dy=−byu0+bxdx
Step 4: Separate variables
We can separate the variables y and x:
dyy=−bdxu0+bx
Step 5: Integrate both sides
Now we integrate both sides:
∫dyy=−b∫dxu0+bx
The left side integrates to:
ln|y|=−b(1bln|u0+bx|)+C
This simplifies to:
ln|y|=−ln|u0+bx|+C
Step 6: Exponentiate to eliminate the logarithm
Exponentiating both sides gives:
|y|=Cu0+bx
Let C be a constant that can take both positive and negative values. Thus, we can write:
y=Cu0+bx
This is the equation of the streamlines.
Step 7: Draw the streamlines
To draw the streamlines for x>0, we can choose different values of C (like C=1,2,−1,−2) and plot the corresponding curves. The streamlines will approach the x-axis as x increases, and they will diverge as y approaches zero.
Summary of the Solution
The equation of the streamlines is given by:
y=Cu0+bx
- v=−by
Topper's Solved these Questions
Similar Questions
The velocity of a particle is given by v=u0+gt+12at2. If its position is x=0 at t=0, then what is its displacement after t=1s ?
View SolutionThe potential energy of a particle of mass m is given by U(x)=U0(1−coscx) where U0 and c are constants. Find the time period of small oscillations of the particle.
View Solution
Knowledge Check
A particle of mass m is moving in a potential well, for which the potential energy is given by U(x)=U0(1−cosax) where U0 and a are positive constants. Then (for the small value of x)
Athe time period of small osciallation is T=2π√maU0Bthe speed of the particle is maximum at x=0Cthe amplitude of oscillations is π8Dthe time period of small osciallations is T=2π√ma2U0Velocity of any fluid particle in a steady incompressible, two dimehsional flow is given by →v=3xˆi−3yˆj
Then resultant streamline (for x>0) can be plotted asA B
B C
C D
D
A particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
A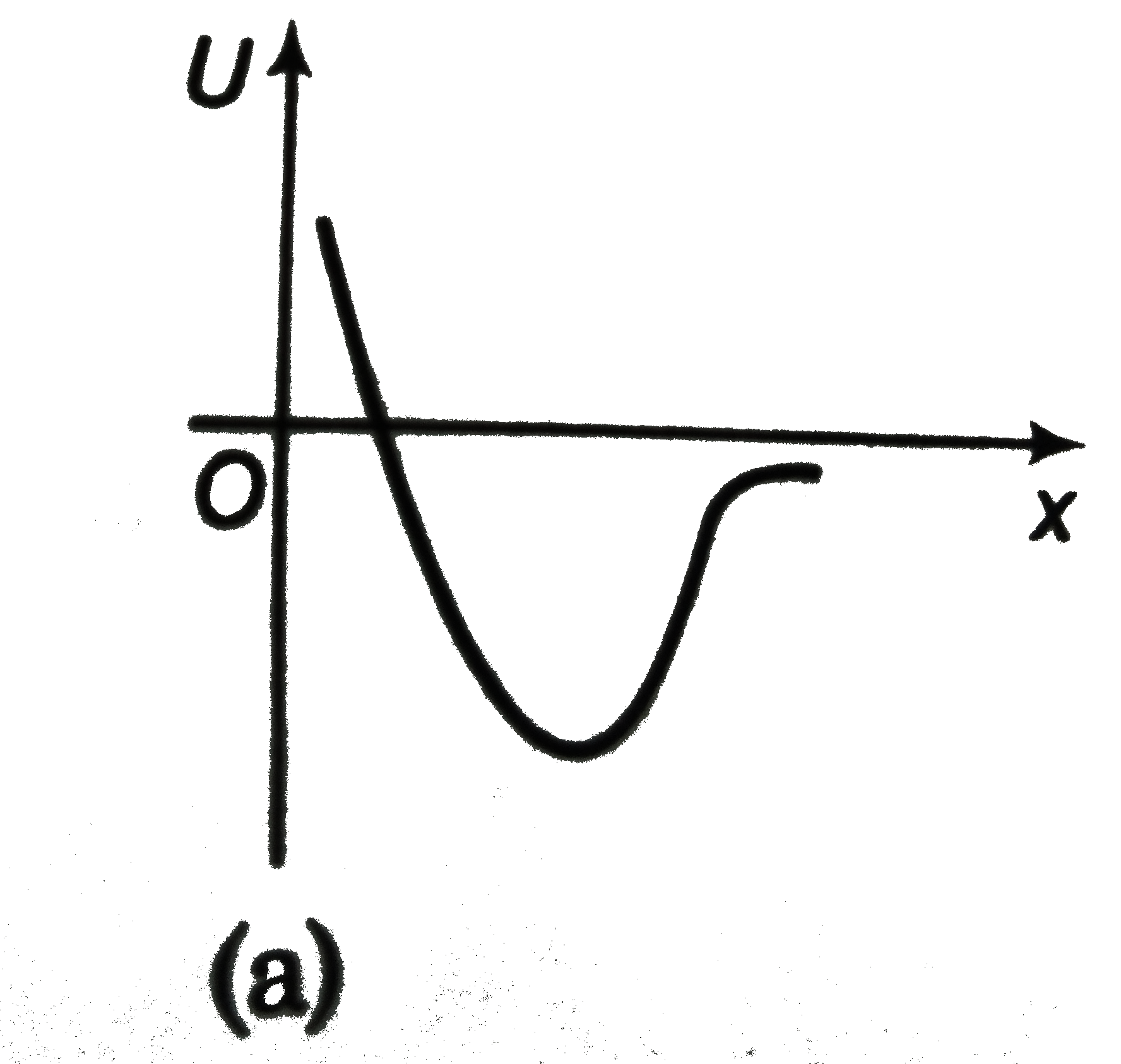 B
B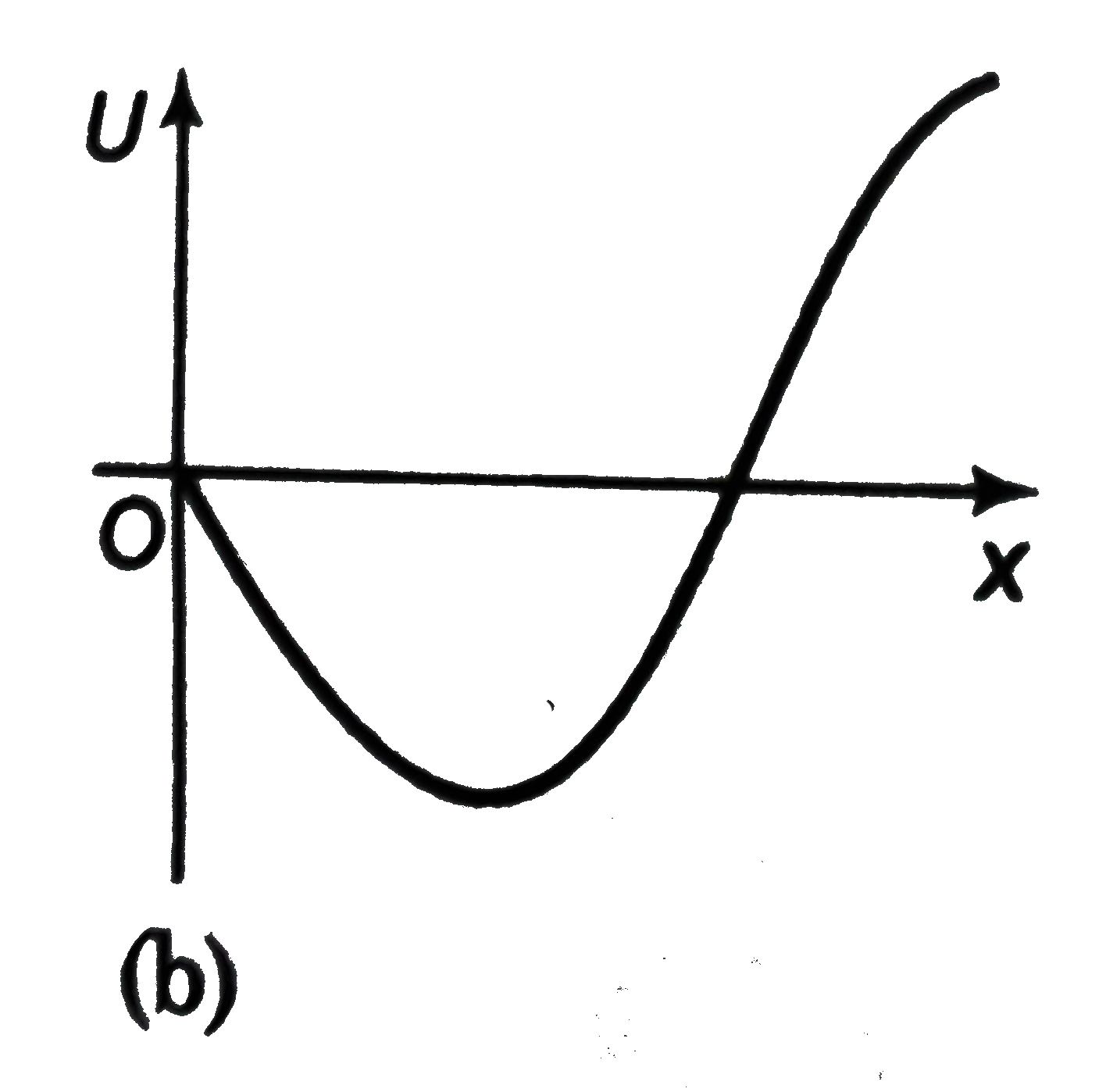 C
C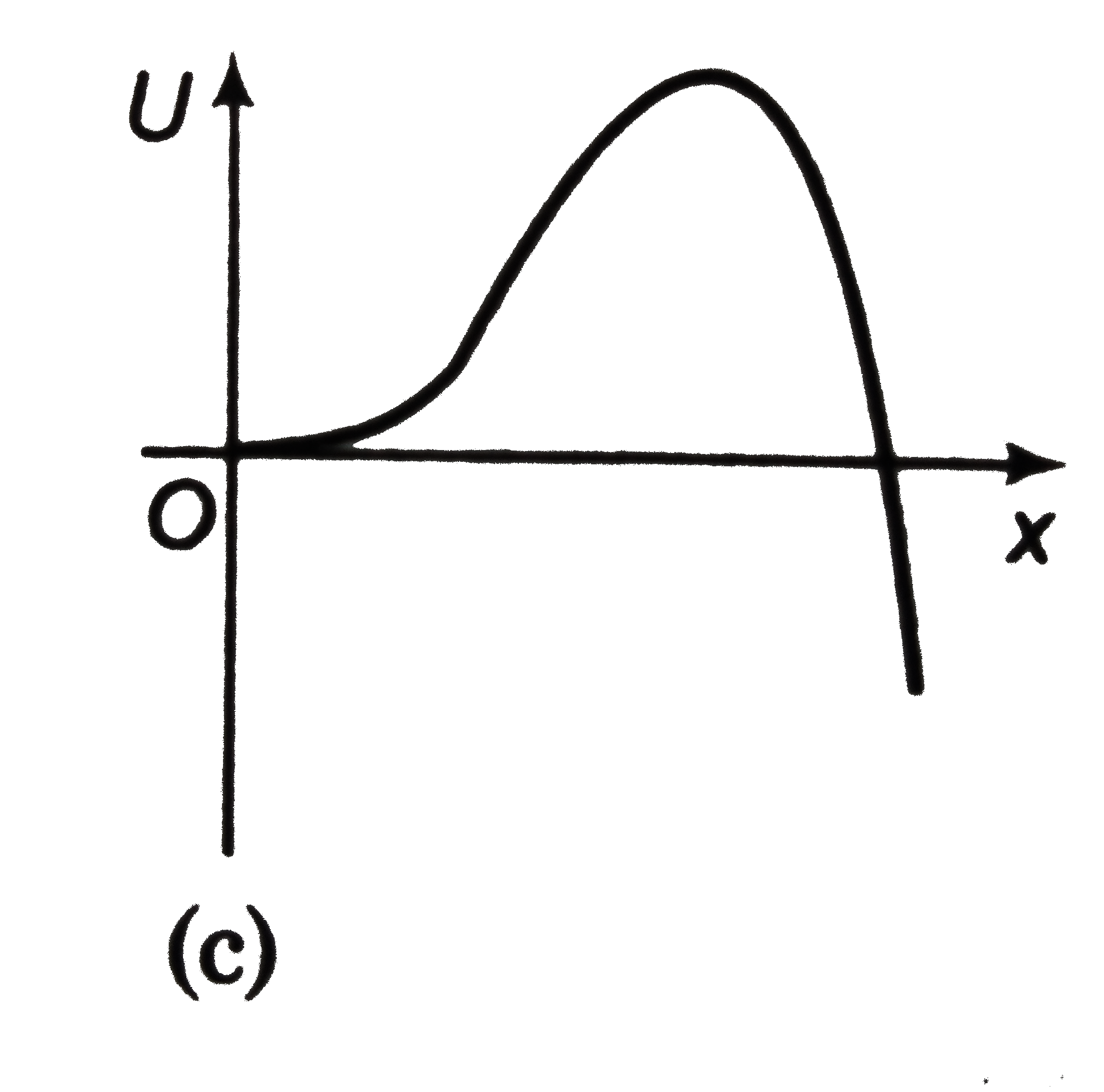 D
D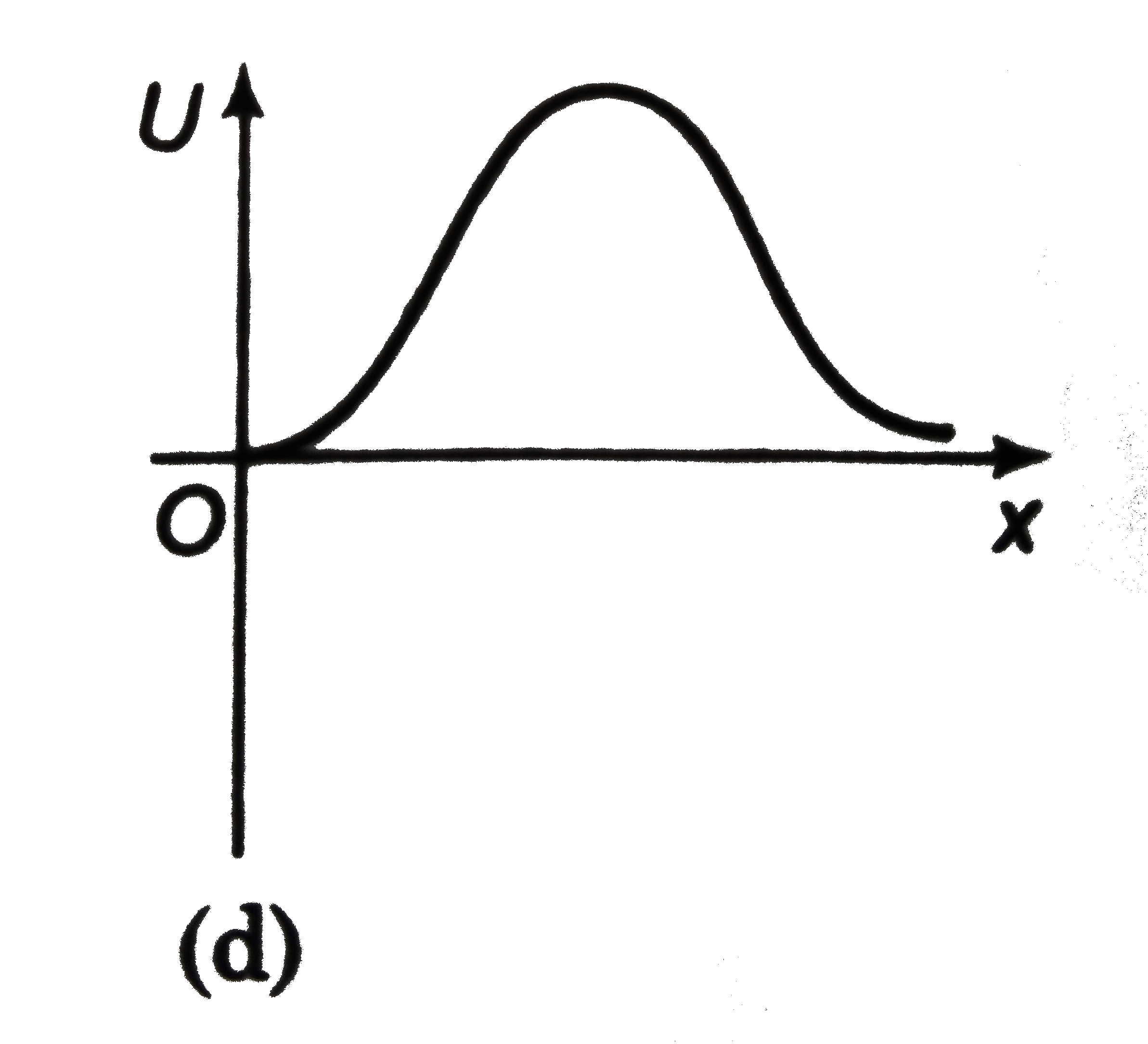
A particle of mass m is located in a unidimensional potential field where potential energy of the particle depends on the coordinates xas:U(x)=U0(1−cosAx),U0 and A constants.
Find the period of small oscillation that the particle performs about the equilibrium position.
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form U(x)=ax2−bx where a and b are positive constants. The position of equilibrium is:
View SolutionThe potential energy of a particle of mass 'm' situated in a unidimensional potential field varies as U(x)=U0[1−cos(ax2)], where U0 and a are positive constant. The time period of small oscillations of the particle about the mean position-
View SolutionIf the velocity (in ms−1 ) of a particle is given by , 4.0ˆi+5.0tˆj then the magnitude of its acceleration (in ms−2) is
View SolutionA particle located in one dimensional potential field has potential energy functionU(x)=ax2−bx3, where a and b are positive constants. The position of equilibrium corresponds to x equal to
View Solution
