In a very long solenoid of radius R, if the magnetic field chabges at the rate of dB/dt.AB=BC
The induced emf for the trianglar circuit ABC shown in Fig. 3.196 is

(a) R2(dBdt)
(b) 4R2(dBdt)
( c) 12R2(dBdt)
(d) 2R2(dBdt)
The correct Answer is:C
( c)|E|=dϕdt=AdBdt=2[12RR]dBdt=R2dBdt
In loop ABC, emf induced due to branch AC is zero and contribution of emf due to ABandBC are equal, hence contribution of emf for the branch is
|E|AB=R22(dBdt)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A cylindrical region of radius R is filled with a uniform magnetic field B as shown in the figure. A metal wire (AB) of length L is placed inside the field such that its ends are symmetrically located with respect to the centre (O) of the circular cross section of the region. If the magnetic field is changed at a rate dBdt the emf induced in the metal wire is e. Find change in value of ε if the wire is displaced by a small distance ΔL parallel to its own length. Assume that the wire remains inside the field region.

View SolutionA uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png)
View Solution
Knowledge Check
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
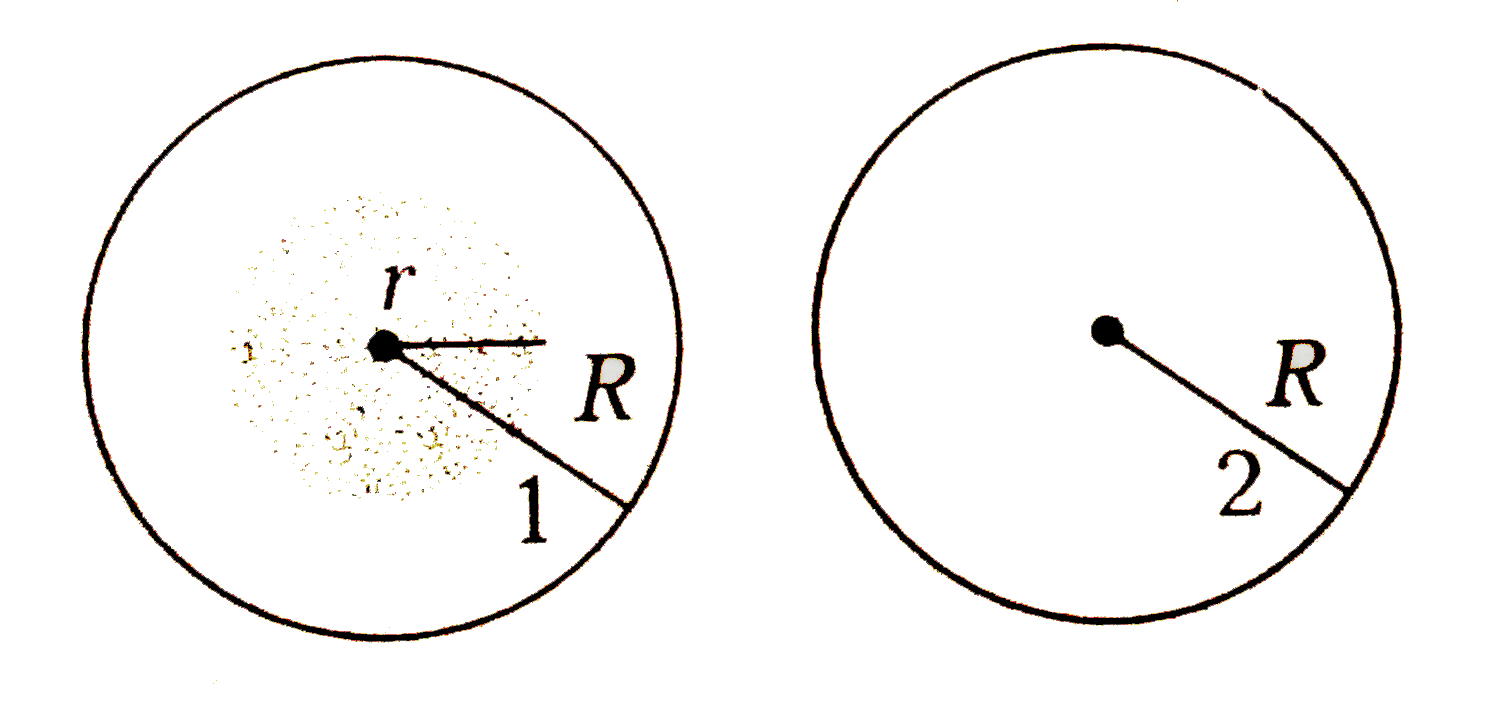 AZero in loop 1 and zero in loop 2B−dBdtπr2 in loop 1 and −dBdtπ2 in loop 2C−dBdtπR2 in loop 1 and zero in loop 2D−dBdtπr2 in loop 1 and zero in loop 2
AZero in loop 1 and zero in loop 2B−dBdtπr2 in loop 1 and −dBdtπ2 in loop 2C−dBdtπR2 in loop 1 and zero in loop 2D−dBdtπr2 in loop 1 and zero in loop 2There is a uniform magnetic field B in a circular region of radius R as shown in Fig. 3.149 whose magnitude changes at the rate of dB/dt. The emf circular concentric conducting arc of radius R1 having an angle θ as shown (−OAO'=θ) is
 A(a) θ2πR21dBdtB(b) θ2R2dBdtC(a) θ2πR2dBdtD(d) none of these
A(a) θ2πR21dBdtB(b) θ2R2dBdtC(a) θ2πR2dBdtD(d) none of theseA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
 A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2
A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2
There is a uniform magnetic field (B) perpendicular to the plane of the figure in a circular region of radius a centred at O. ABCD is a conducing loop in the plane of the figure with its arms BC and DA along two radial lines from O having an angle θ between them. AB is circular arc of radius OB = d centred at O. CD is also a circular arc of radius OC=b centred at O. The magnetic field is changed at a rate dBdt.
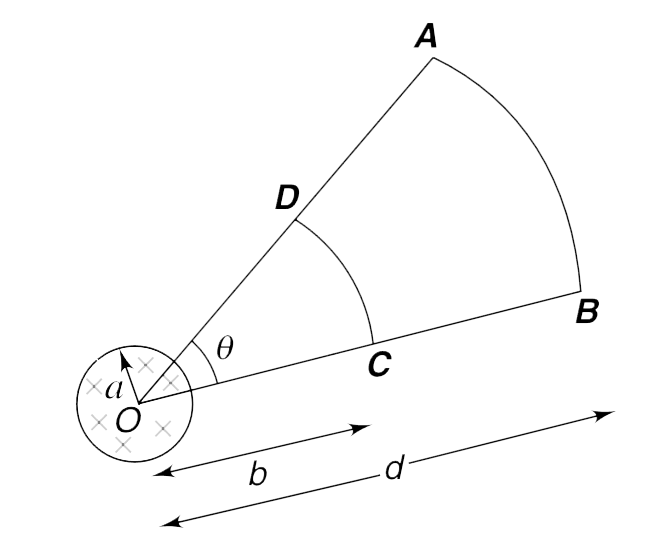
(a) The emf induced in the loop ABCD.
(b) Find emf induced in arc AB.
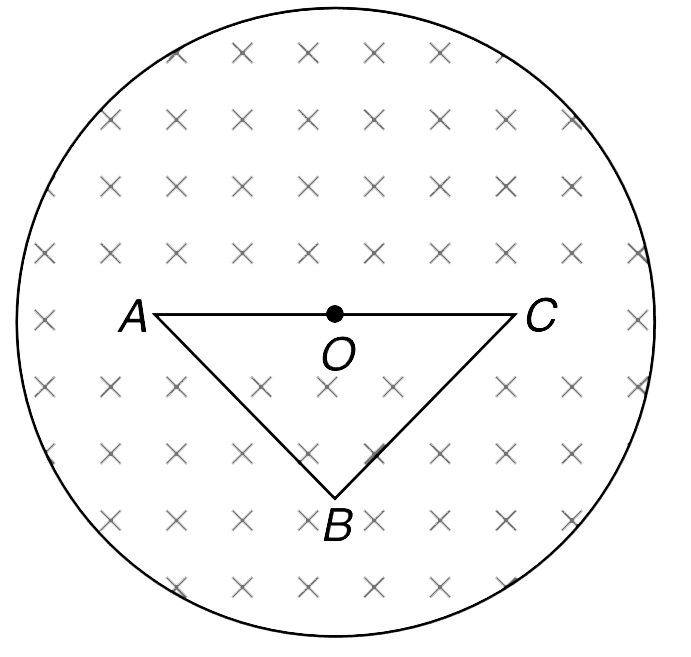
View SolutionA uniform magnetic field B exists in a region of circular cross section of radius R. The field is directed perpendicularly into the plane of the figure. There is a tri- angular circuit ABC made of a uniform wire placed in the circular region. The triangle is a right angled isosceles tri- angle with equal sides AB=BC=l. The hypotenuse AC has its midpoint at the centre of the circle. Electrical resistance of the triangular circuit per unit length isr0l. If the magnetic field is changed at a constant rate of dBdt=α, find the potential difference between points C and A and that between B and A.
View SolutionA nonconducting of radius r has charge Q. A magnetic field perpendicular to the plane of ring changes at the rate dBdt. The torque experienced by the ring is
View SolutionA conducing circular loop is placed in a uniform magnetic field of indution B tesla with its plane normal to the field. Now, radius of the loop starts shrinking at the rate (dr/dt). Then the induced e.m.f. at the instant when the radius is r is:
View SolutionA uniform magneitc field B fills a cylindrical volume of radius R, A metal rod of length l is placed as shown. If B is changing at the rate of dB/dt, the emf that is produced by the changing magnetic field is ξ here p = √R2−(l2)2. then
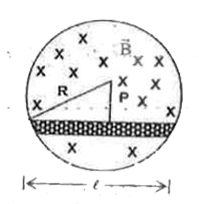
View Solution
