In a Young's double slit experiment the separation between the slits is 0.10 mm, the wavelength of light used is 600 nm and the interference pattern is observed on a screen 1.0 m away. Find the separation between the successive bright fringes.
To solve the problem of finding the separation between successive bright fringes in a Young's double slit experiment, we will use the formula for fringe width (β):
1. Identify the given values:
- Separation between the slits (d) = 0.10 mm = 0.10×10−3 m = 1.0×10−4 m
- Wavelength of light (λ) = 600 nm = 600×10−9 m
- Distance from the slits to the screen (D) = 1.0 m
2. Write the formula for fringe width (β):
β=D⋅λd
where:
- β = fringe width (separation between successive bright fringes)
- D = distance from the slits to the screen
- λ = wavelength of light
- d = separation between the slits
3. Substitute the values into the formula:
β=1.0m⋅600×10−9m0.10×10−3m
4. Calculate the numerator:
1.0m⋅600×10−9m=600×10−9m
5. Calculate the denominator:
0.10×10−3m=1.0×10−4m
6. Now compute β:
β=600×10−91.0×10−4=6000×10−5=0.06m=6cm
7. Final answer:
The separation between successive bright fringes is 6 cm.
- Separation between the slits (d) = 0.10 mm = 0.10×10−3 m = 1.0×10−4 m
- Wavelength of light (λ) = 600 nm = 600×10−9 m
- Distance from the slits to the screen (D) = 1.0 m
β=D⋅λd
where:
- β = fringe width (separation between successive bright fringes)
- D = distance from the slits to the screen
- λ = wavelength of light
- d = separation between the slits
β=1.0m⋅600×10−9m0.10×10−3m
1.0m⋅600×10−9m=600×10−9m
0.10×10−3m=1.0×10−4m
β=600×10−91.0×10−4=6000×10−5=0.06m=6cm
The separation between successive bright fringes is 6 cm.
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - worked out Examples
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -1
17 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
In a double slit interference experiment, the separation between the slits is 1.0 mm, the wavelength of light used is 5.0x10−7 m and the distance of the screen from the slits is 1.0 m. (a) Find the distance of the centre of the first minimum from the centre of the central maximum. (b) How many bright fringes are formed in one centimeter width on the screen ?
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, if the distance between two slits is equal to the wavelength of used light. Then the maximum number of bright firnges obtained on the screen will be
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
View SolutionIn Young's double-slit experiment, the separation between the slits is d, distance between the slit and screen is D(D>>d), In the interference pattern, there is a maxima exactly in front of each slit. Then the possilbe wavelength(s) used in the experiment are
View SolutionIn a Young's double-slit experiment the fringe width is 0.2mm. If the wavelength of light used is increased by 10% and the separation between the slits if also increased by 10%, the fringe width will be
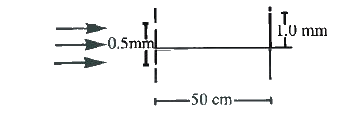
View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
View Solution
