Is the formula "Real depth/Apparent depth =μ. valid if viewed from a position quite away from the normal ?
To determine if the formula "Real depth/Apparent depth = μ" is valid when viewed from a position quite away from the normal, we need to analyze the concepts of real depth, apparent depth, and the refractive index (μ) in the context of refraction.
1. Understanding Real and Apparent Depth:
- Real depth is the actual depth of an object submerged in a medium (like water).
- Apparent depth is how deep the object appears to be when viewed from above the surface of the medium.
2. Refraction of Light:
- When light travels from one medium to another (e.g., from water to air), it bends at the interface due to a change in speed. This bending of light is described by Snell's Law.
3. Snell's Law:
- Snell's Law states that n1sin(θ1)=n2sin(θ2), where n1 and n2 are the refractive indices of the two media, and θ1 and θ2 are the angles of incidence and refraction, respectively.
4. Deriving the Formula:
- The formula "Real depth/Apparent depth = μ" is derived under the assumption that the observer is looking straight down (normal incidence). Here, μ is the refractive index of the medium relative to air.
5. Effect of Viewing Angle:
- When viewed from a position away from the normal, the angle of incidence changes, which affects the angle of refraction. This means that the apparent depth will not be simply related to the real depth by the refractive index in the same way as when viewed from directly above.
6. Conclusion:
- The formula "Real depth/Apparent depth = μ" is valid only when the observer is looking directly down (normal incidence). If the observer is at an angle, the relationship becomes more complex, and the formula does not hold true.
Final Answer:
No, the formula "Real depth/Apparent depth = μ" is not valid if viewed from a position quite away from the normal.
- Real depth is the actual depth of an object submerged in a medium (like water).
- Apparent depth is how deep the object appears to be when viewed from above the surface of the medium.
- When light travels from one medium to another (e.g., from water to air), it bends at the interface due to a change in speed. This bending of light is described by Snell's Law.
- Snell's Law states that n1sin(θ1)=n2sin(θ2), where n1 and n2 are the refractive indices of the two media, and θ1 and θ2 are the angles of incidence and refraction, respectively.
- The formula "Real depth/Apparent depth = μ" is derived under the assumption that the observer is looking straight down (normal incidence). Here, μ is the refractive index of the medium relative to air.
- When viewed from a position away from the normal, the angle of incidence changes, which affects the angle of refraction. This means that the apparent depth will not be simply related to the real depth by the refractive index in the same way as when viewed from directly above.
- The formula "Real depth/Apparent depth = μ" is valid only when the observer is looking directly down (normal incidence). If the observer is at an angle, the relationship becomes more complex, and the formula does not hold true.
No, the formula "Real depth/Apparent depth = μ" is not valid if viewed from a position quite away from the normal.
Topper's Solved these Questions
Similar Questions
A ray travelling from glass to air, bends away from the normal. ____
View SolutionThe angle of elevation of top of a tower from a point on the ground is 30∘ and it is 60∘ when it is viewed from a point located 40 m away from the initial point towards the tower the height of the tower is
View SolutionProve that
Refractive index=real depthapparent depth
View SolutionA plane wave of sound travelling in air is incident upon a plane water surface. The angle of incidence is 60∘. Assuming snell's law to be valid for sound waves, it follows that the sound wave will be refracted into water away from the normal.
View SolutionA sphere made of transparent material of refractive index (μ=32 )and of radius 50 cm has a small air bubble 10 cm below the surface. The apparent depth of the bubble if viewed from outside normally is
View SolutionA small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
View SolutionA mark on the surface of a glass spehre (μ=1.5) is viewed from a diametrically opposite position. It appears to be at a distance 10 cm from its actual position. The radius of the sphere is
View SolutionWhen a ray of light travels obliquely from a rarer medium to a denser medium, it bends away from the normal.
View SolutionThe apparent depth of an object O from AB is
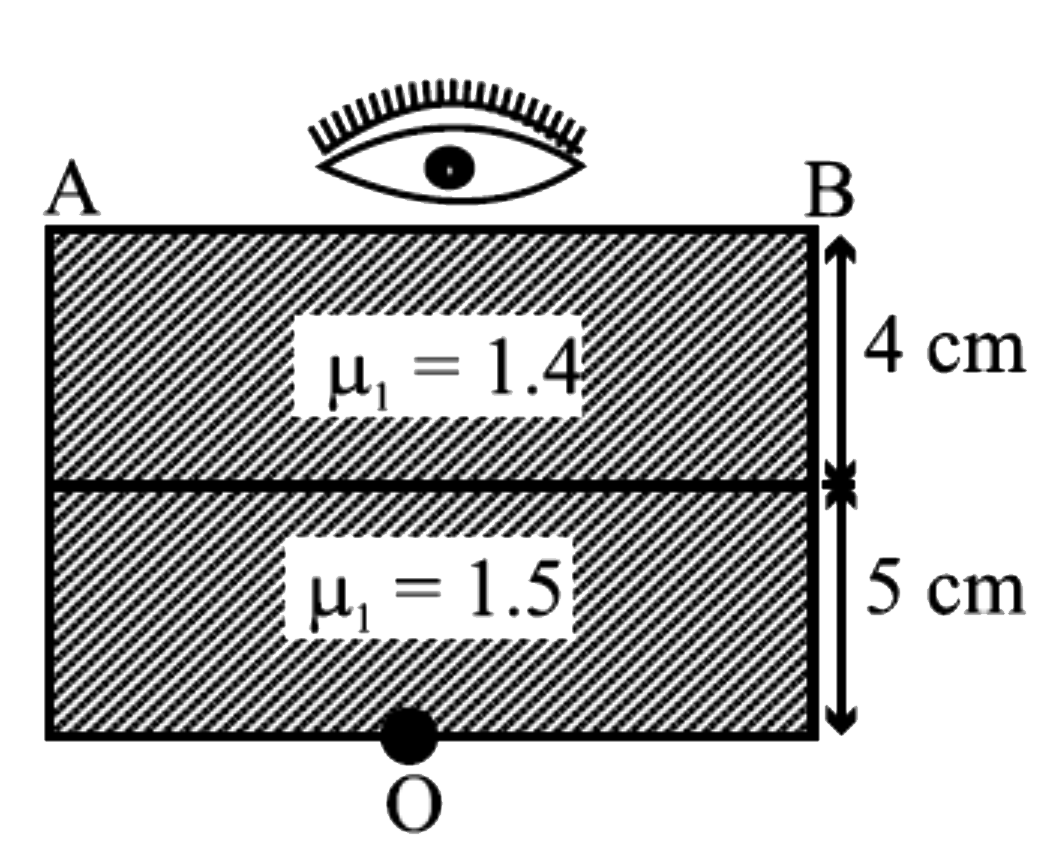
View SolutionHow does the pressure at a certain depth in water differ from that of the same depth in river water. Explain year answer.
View Solution
