In an adiabatic process, the state of a gas is changed from P1,V1,T1,toP2,V2,T2. Which of the following relation is correct
T1Vγ−11=T2Vγ−12
P1Vγ−11=P2Vγ−12
T1Pγ1=T2P2
T1Vγ1=T2Vγ2
The correct Answer is:A
Step by step video, text & image solution for In an adiabatic process, the state of a gas is changed from P_(1),V_(1),T_(1), "to" P_(2),V_(2),T_(2). Which of the following relation is correct by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINETIC THEORY OF GASES AND RADIATION BOOK - TARGET PUBLICATIONCHAPTER - KINETIC THEORY OF GASES AND RADIATION EXERCISE - critical thinking
104 Videos
- KINETIC THEORY OF GASES AND RADIATION BOOK - TARGET PUBLICATIONCHAPTER - KINETIC THEORY OF GASES AND RADIATION EXERCISE - Competitive thinking
187 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - TARGET PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - EVALUATION TEST
20 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - EVALUATION TEST
19 Videos
Similar Questions
For an ideal gas, an illustration of the different paths, A (B+C) and (D+E) from an intial state P1,V1,T1 to a final state P2,V2,T1 as shown in the given figure.
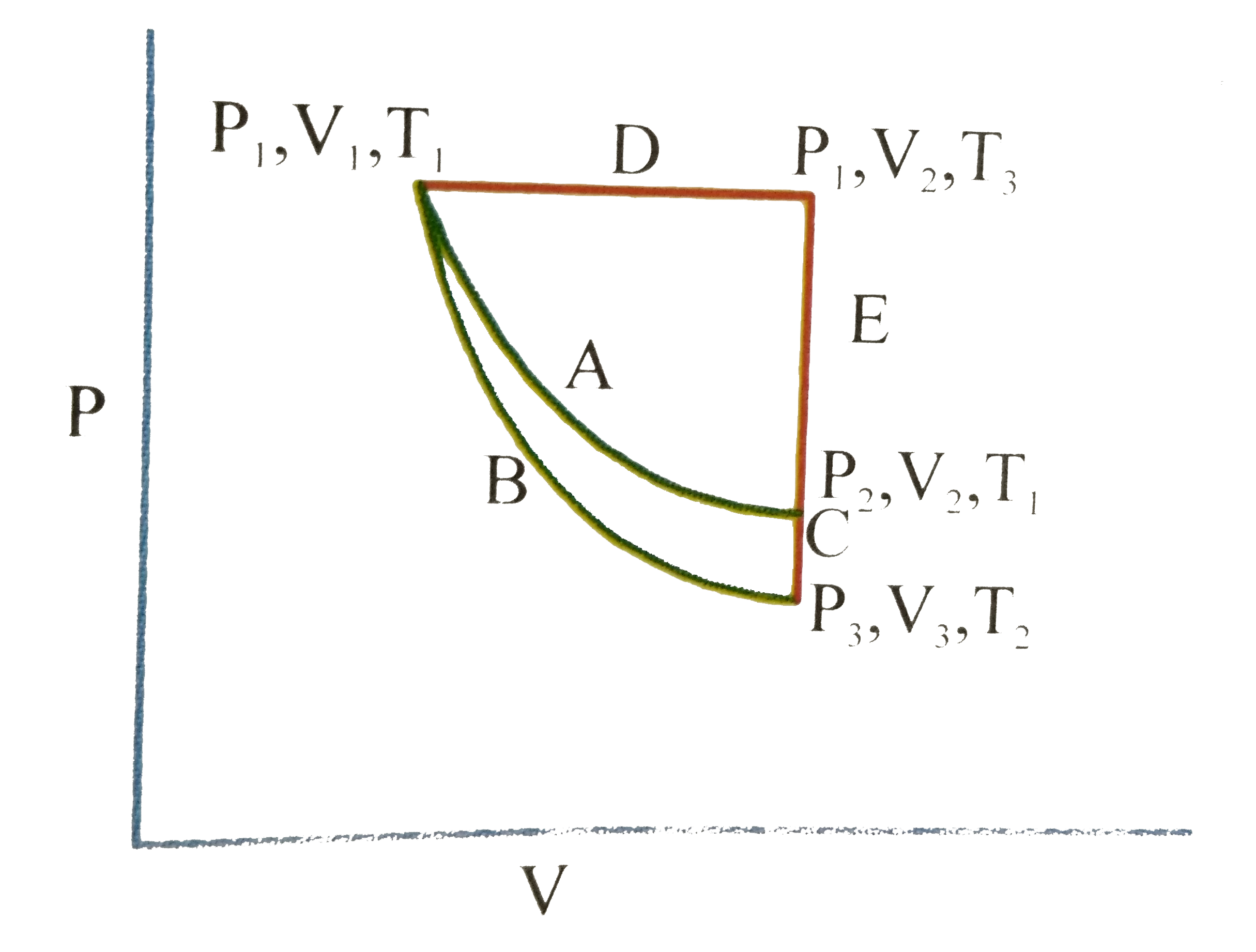
Path (A) represents a reversible isothernal expanison from P1V1 to P2V2. Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating the gas at constant volume (C) from P3,V2,T2 to P2,V2T1 to P1,V2,T3 followed by reversible cooling at a constant volume V2 (E) from P1,V2,T3 to P2,V2,T1
What is ΔS for path (D+E) ?
View SolutionP1V1T1=P2V2T2 is -
View Solution
Knowledge Check
For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
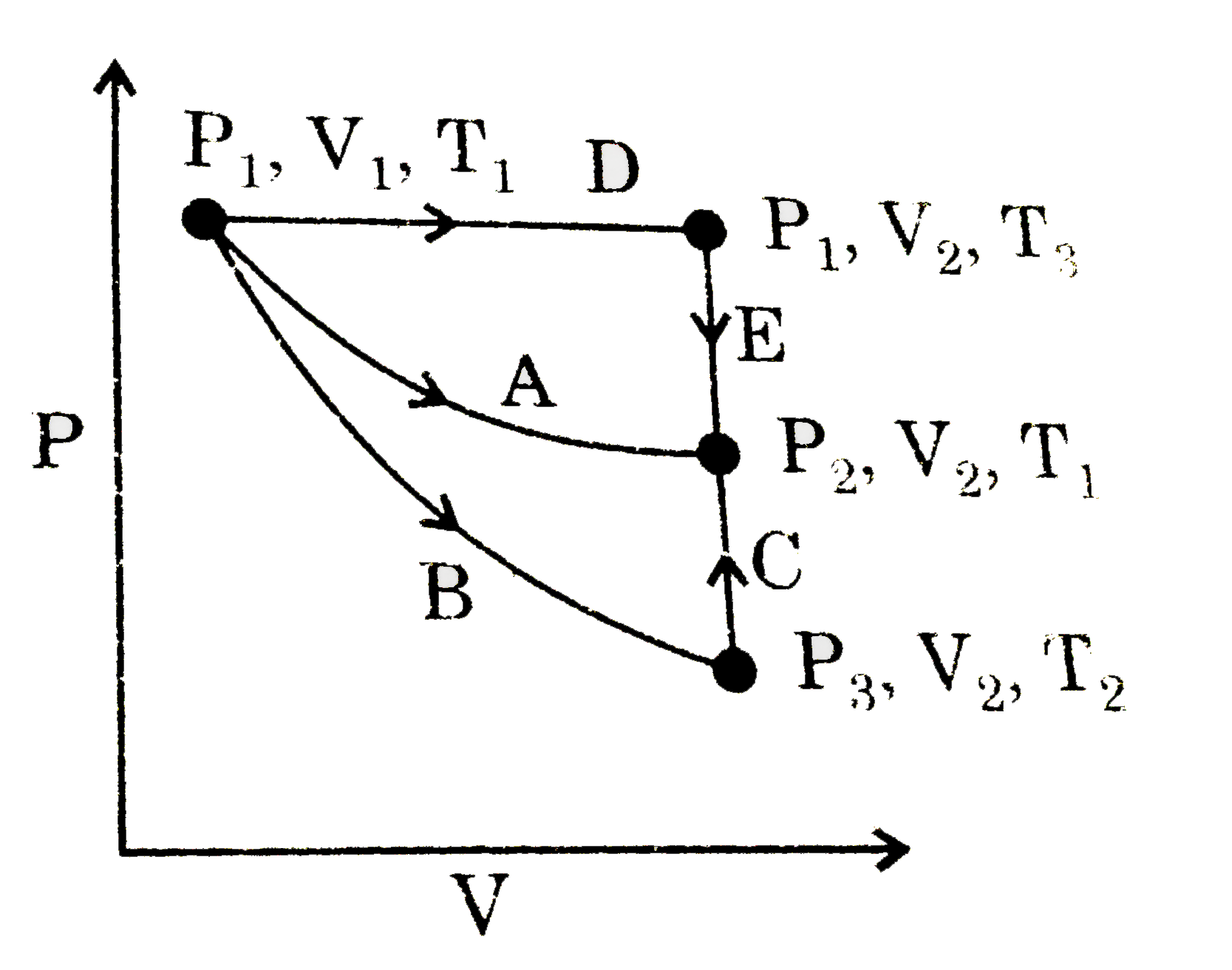
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?AzeroB−nR InV2V1C−nRT1 InV2V1DnRT1 InV2V1For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
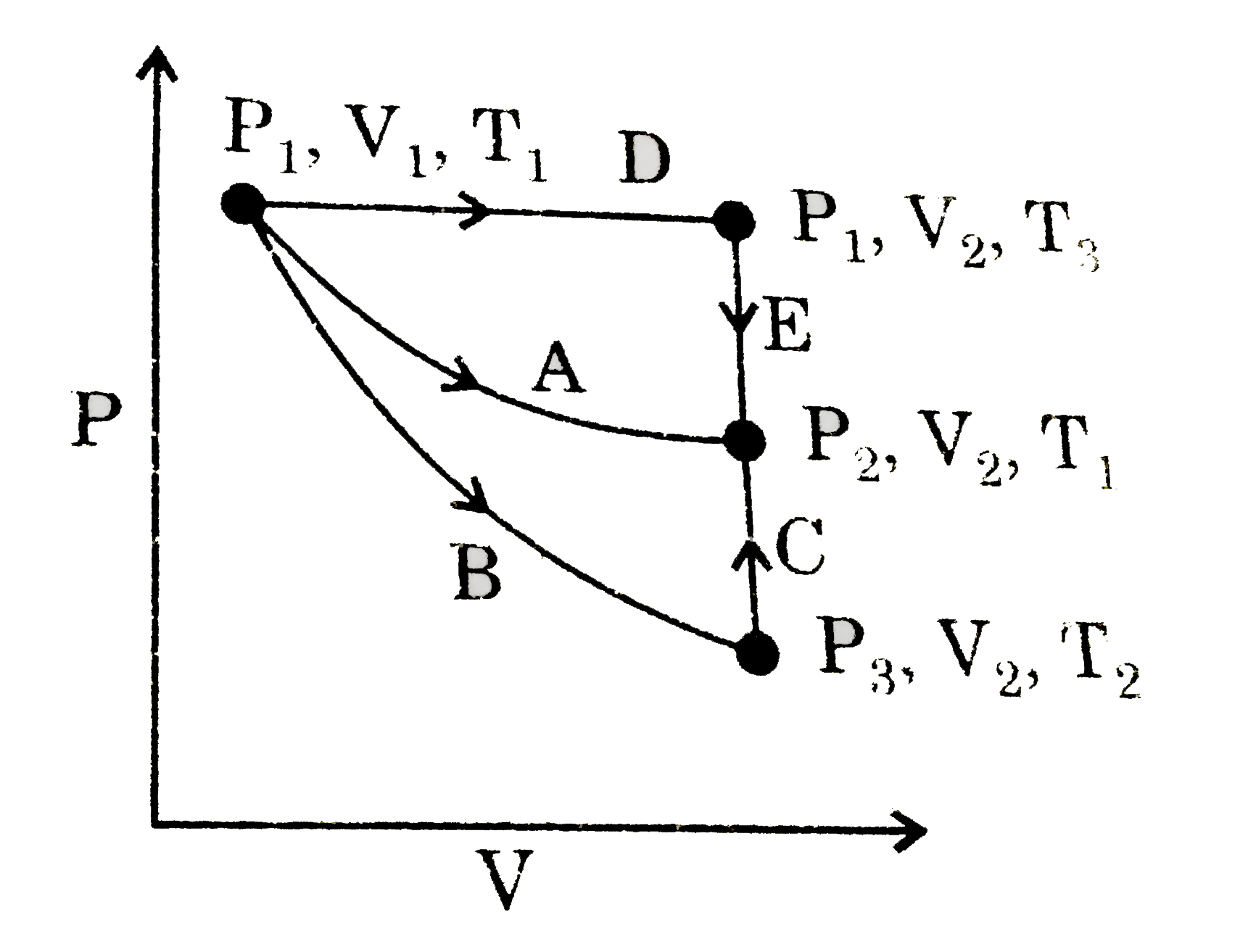
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?AzeroB∫T1T3CV(T)TdtC−nR InV2V1DnR InV2V1For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?Anr InV2V1B−nr InV2V1CzeroDnR(V2−V1)
An ideal gas follows a process described by PV2=C from (P1,V1,T1) to (P2,V2,T2) (C is a constant). Then
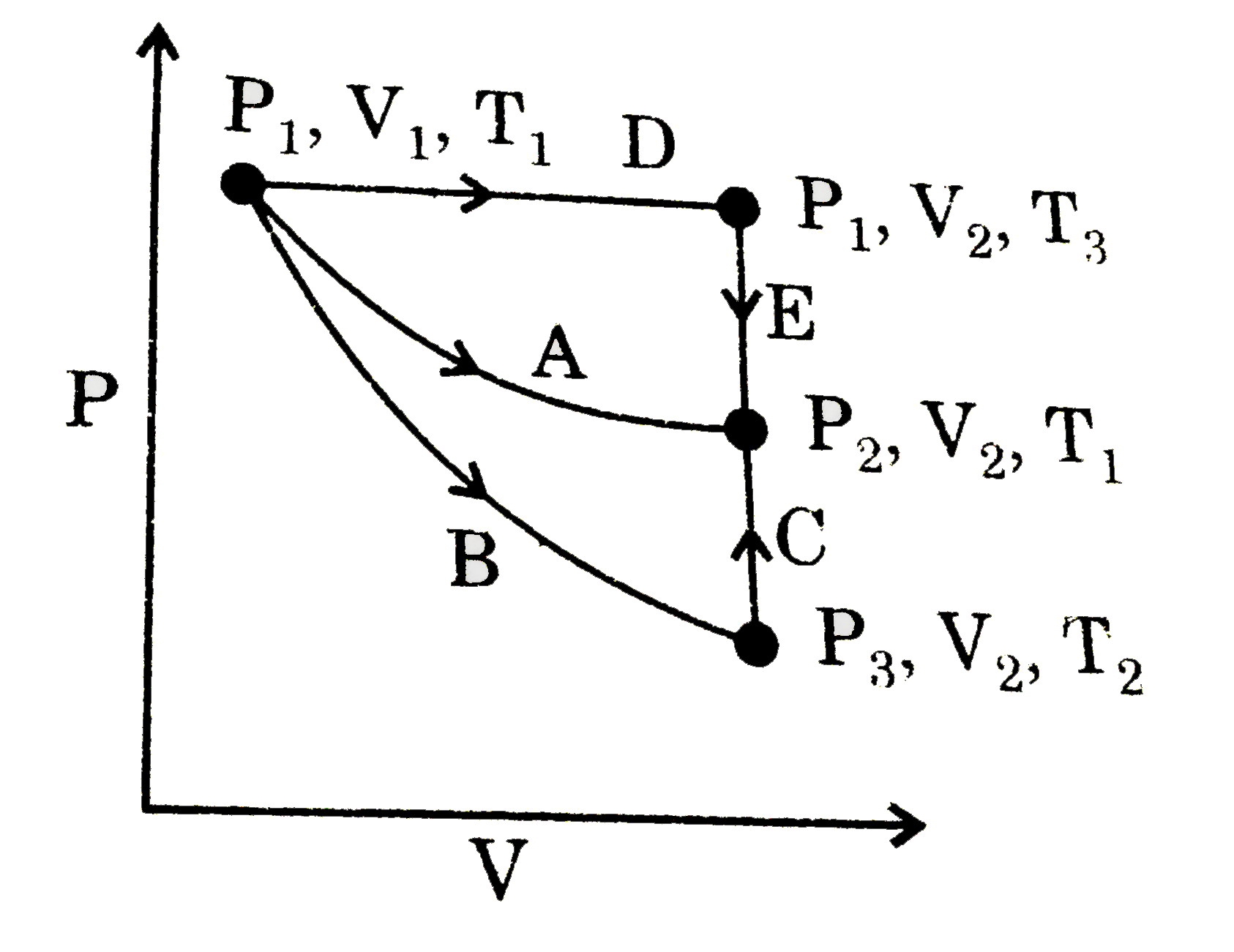
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
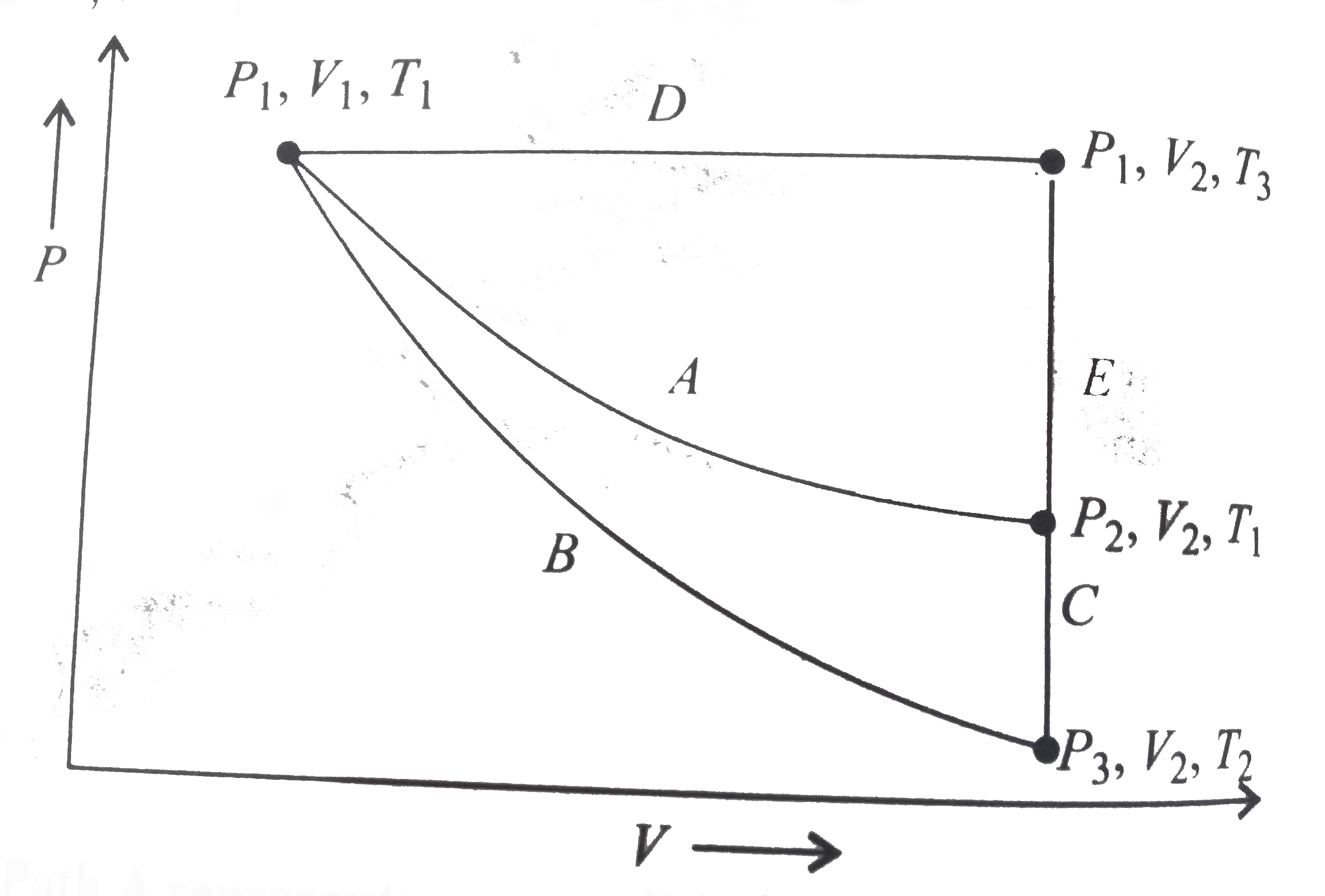
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
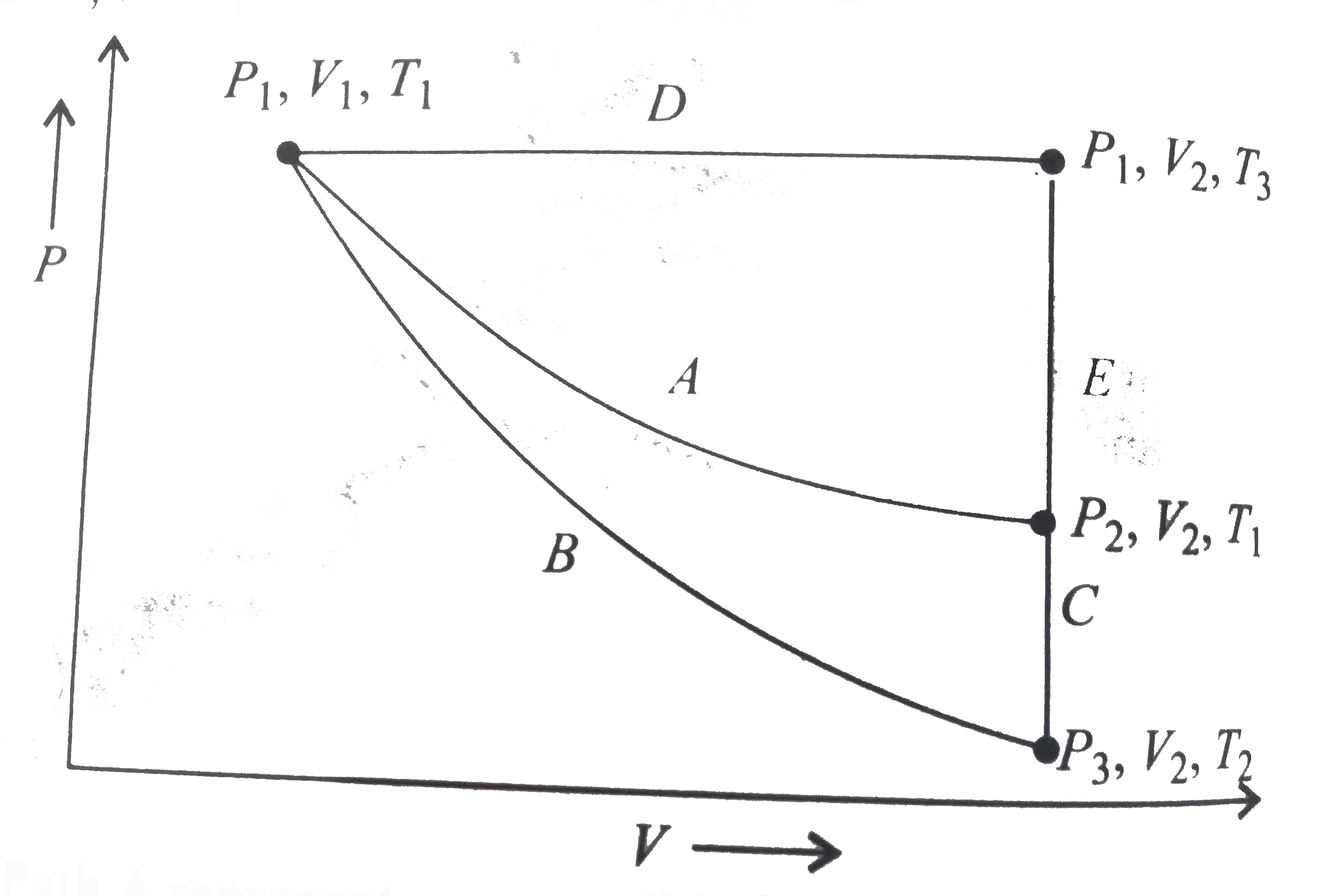
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
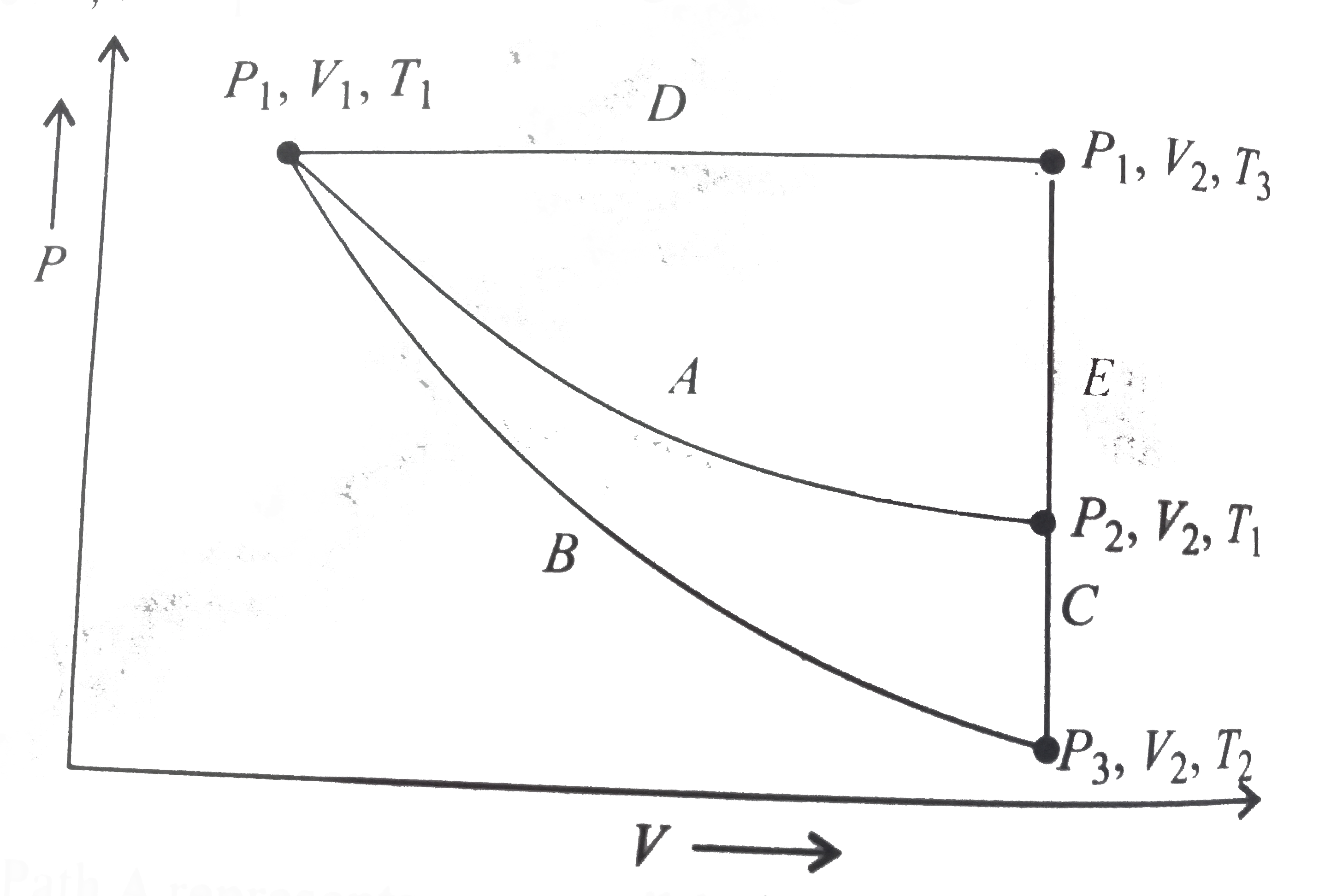
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
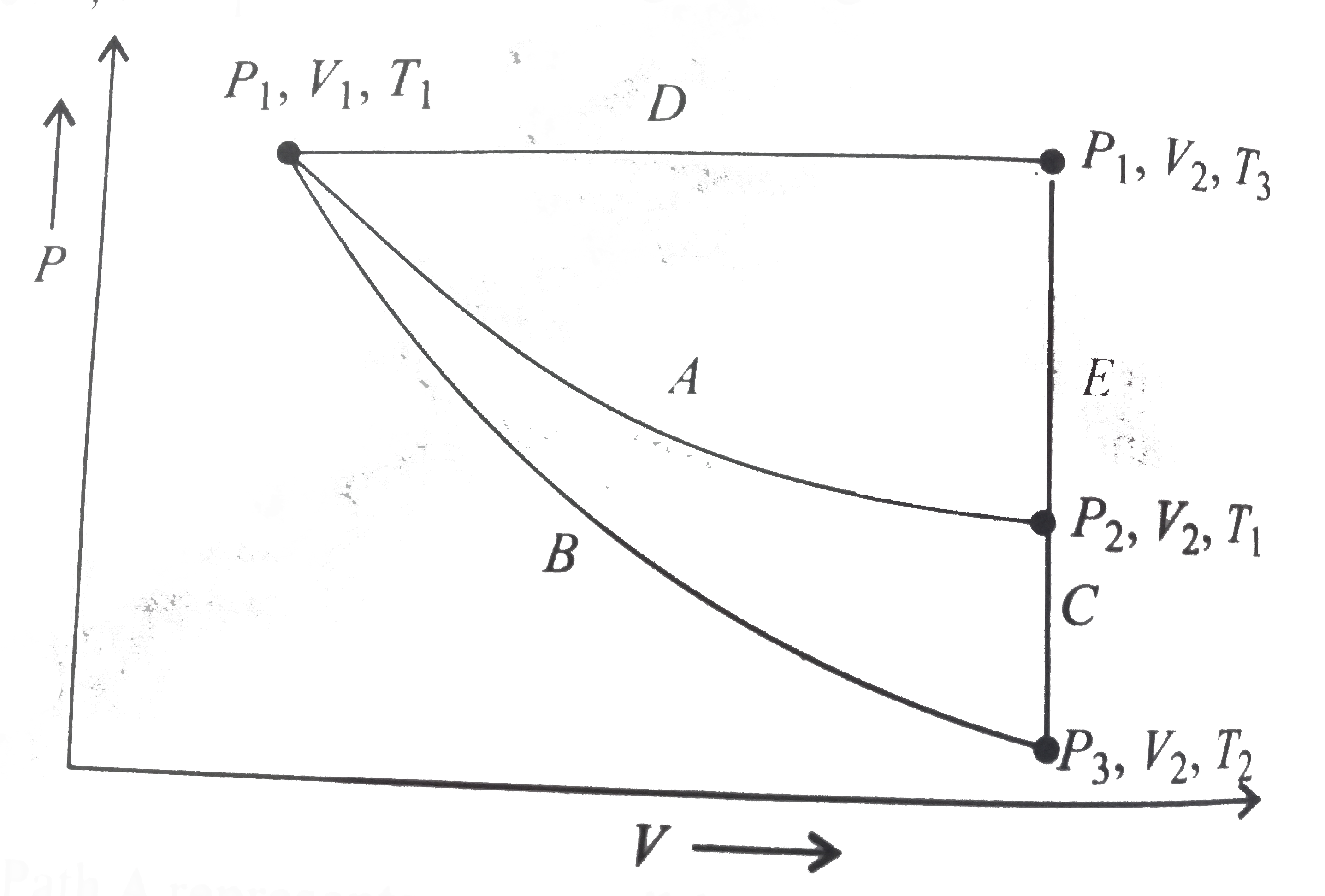
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (B+C)?
View Solution
