In an ΔABC as showin in Fig. 2 . (2) .71 (a) prove
that asinA=bsinB=CsinC.
Video Solution
Text Solution
From polygon law of vector addition we can see AB+BC+CA=0
∴cˆi+(asinBˆj−acosBˆi)
+(−bcosAˆi−bsinAˆj)=0
∴(c−acosB−bcosA)ˆi
+(asinB−bsinA)ˆj=0
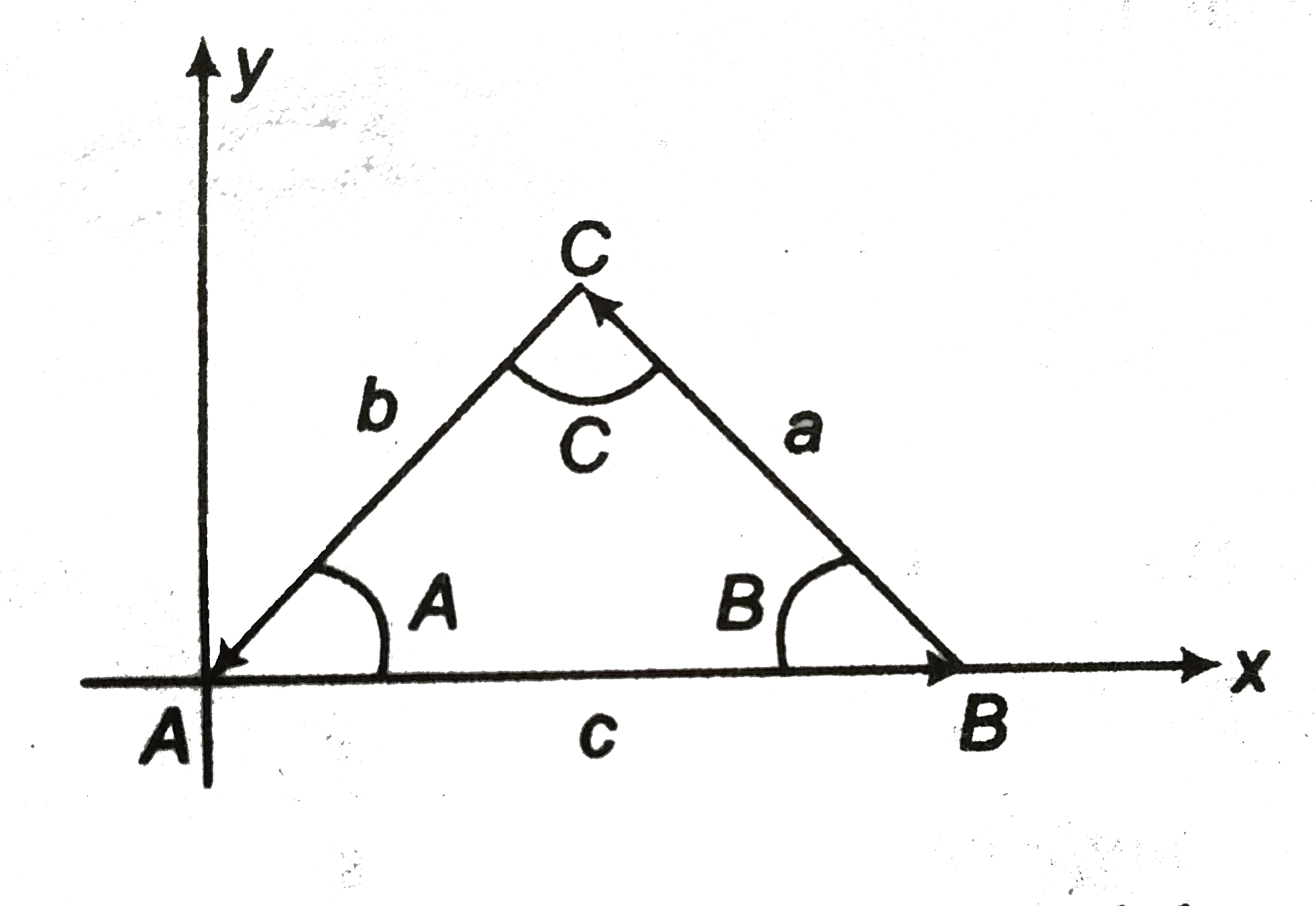
Putting coefficient of ˆj=0, we find that,
asinA=bsinB
Now taking B as origin and BC as the x-axis, we can
prove other relation.
|
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example
40 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - check point 2.1
15 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Single Correct
39 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
In any Δ ABC,∑ a sin (B -C) =
View SolutionIn any Δ ABC, ∑ a(sin B - sin C) =
View SolutionLet a,b, c are the sides opposite to angles A, B , C respectively in a ΔABCtanA−B2=a−ba+bcotC2andasinA=bsinB=csinC,
If a=6,b=3andcos(A−B)=45
Valus of sin A is equal to
View SolutionIn a ΔABC, show that 2R2sinAsinBsinC=Δ.
View SolutionIn any triangle ABC ,prove that a−bcosCc−bcosA=sinCsinA
View SolutionIn a ∆ABC prove that cos(A+B2)=sin(C)2
View SolutionIn any triangle ABC, show that : 2acos(B2)cos(C2)=(a+b+c)sin(A2)
View SolutionIn a ΔABC, 2sinAcosB+2sinBcosC+2sinCcosA = sinA+sinB+sinC, then ΔABC is (a) Isoceles (b) Right Angled (c) Acute (d) None of these
View SolutionIn a triangle ABC,2acsin(12(A−B+C))=
View SolutionIn any triangle ABC, prove that: sin(B−C)sin(B+C)=b2−c2a2
View Solution
