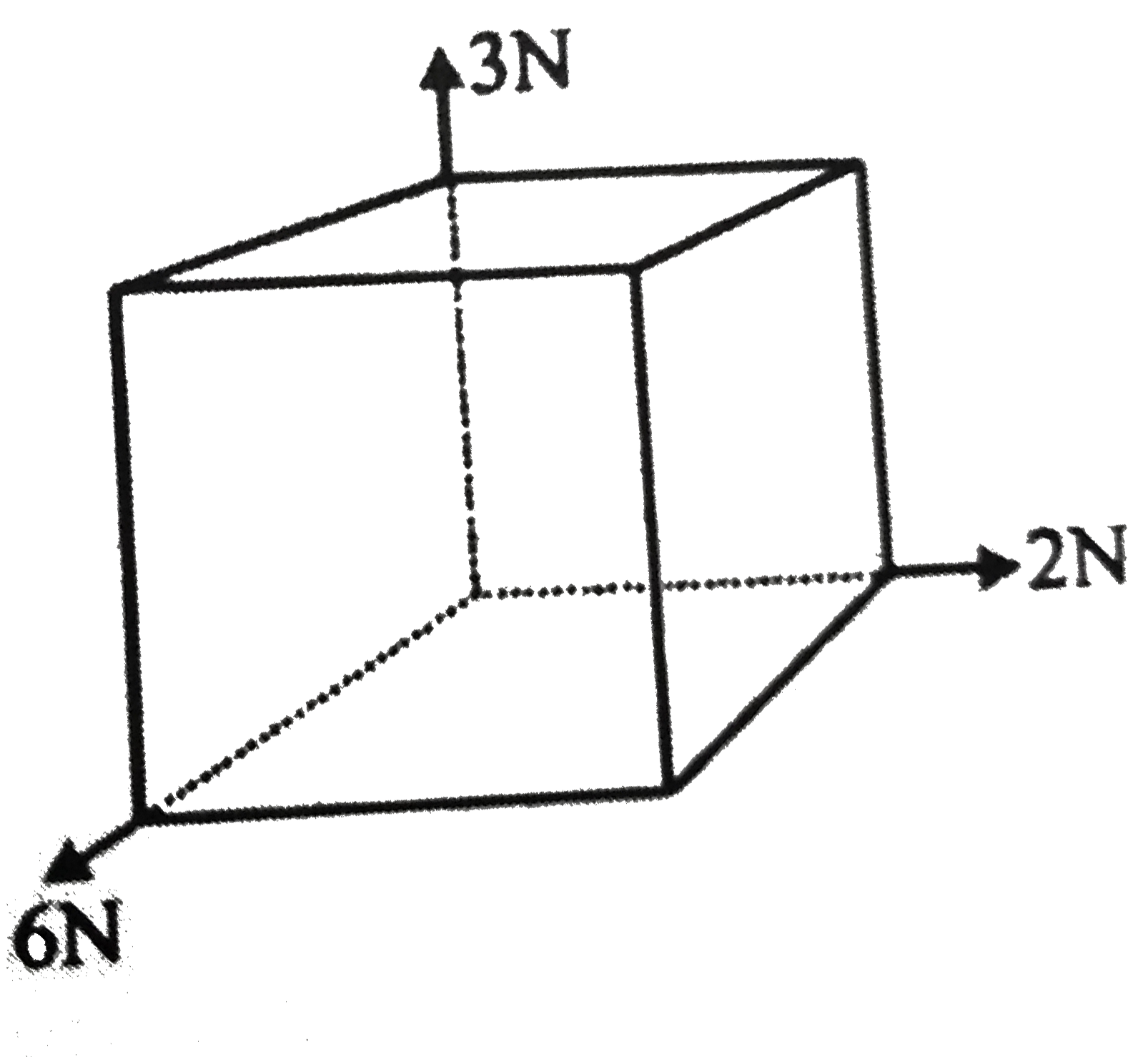
Four forces of magnitude P, 2P, 3P and 4P act along the four sides of a square ABCD in cyclic order. Use the vector method to find the magnitude of resultant force.
The correct Answer is:B
To solve the problem of finding the resultant force acting on a square ABCD due to the forces of magnitudes P, 2P, 3P, and 4P, we will use vector addition. The forces act along the sides of the square in a cyclic order.
1. Identify the Forces and Directions:
- Let’s denote the forces acting on the square:
- Force F1=P acting to the right along side AB.
- Force F2=2P acting upwards along side BC.
- Force F3=3P acting to the left along side CD.
- Force F4=4P acting downwards along side DA.
2. Assign Coordinate Directions:
- We will use a Cartesian coordinate system:
- Right (along AB) is the positive x-direction.
- Up (along BC) is the positive y-direction.
- Left (along CD) is the negative x-direction.
- Down (along DA) is the negative y-direction.
3. Express Forces as Vectors:
- Convert each force into vector form:
- →F1=P^i
- →F2=2P^j
- →F3=−3P^i
- →F4=−4P^j
4. Sum the Forces:
- The resultant force →R can be found by summing all the forces:
→R=→F1+→F2+→F3+→F4
→R=(P−3P)^i+(2P−4P)^j
→R=−2P^i−2P^j
5. Calculate the Magnitude of the Resultant Force:
- The magnitude of the resultant vector →R is given by:
|→R|=√(−2P)2+(−2P)2
|→R|=√4P2+4P2=√8P2=2√2P
Final Result:
The magnitude of the resultant force is 2√2P.
---
- Let’s denote the forces acting on the square:
- Force F1=P acting to the right along side AB.
- Force F2=2P acting upwards along side BC.
- Force F3=3P acting to the left along side CD.
- Force F4=4P acting downwards along side DA.
- We will use a Cartesian coordinate system:
- Right (along AB) is the positive x-direction.
- Up (along BC) is the positive y-direction.
- Left (along CD) is the negative x-direction.
- Down (along DA) is the negative y-direction.
- Convert each force into vector form:
- →F1=P^i
- →F2=2P^j
- →F3=−3P^i
- →F4=−4P^j
- The resultant force →R can be found by summing all the forces:
→R=→F1+→F2+→F3+→F4
→R=(P−3P)^i+(2P−4P)^j
→R=−2P^i−2P^j
- The magnitude of the resultant vector →R is given by:
|→R|=√(−2P)2+(−2P)2
|→R|=√4P2+4P2=√8P2=2√2P
The magnitude of the resultant force is 2√2P.
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example
40 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - check point 2.1
15 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Single Correct
39 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
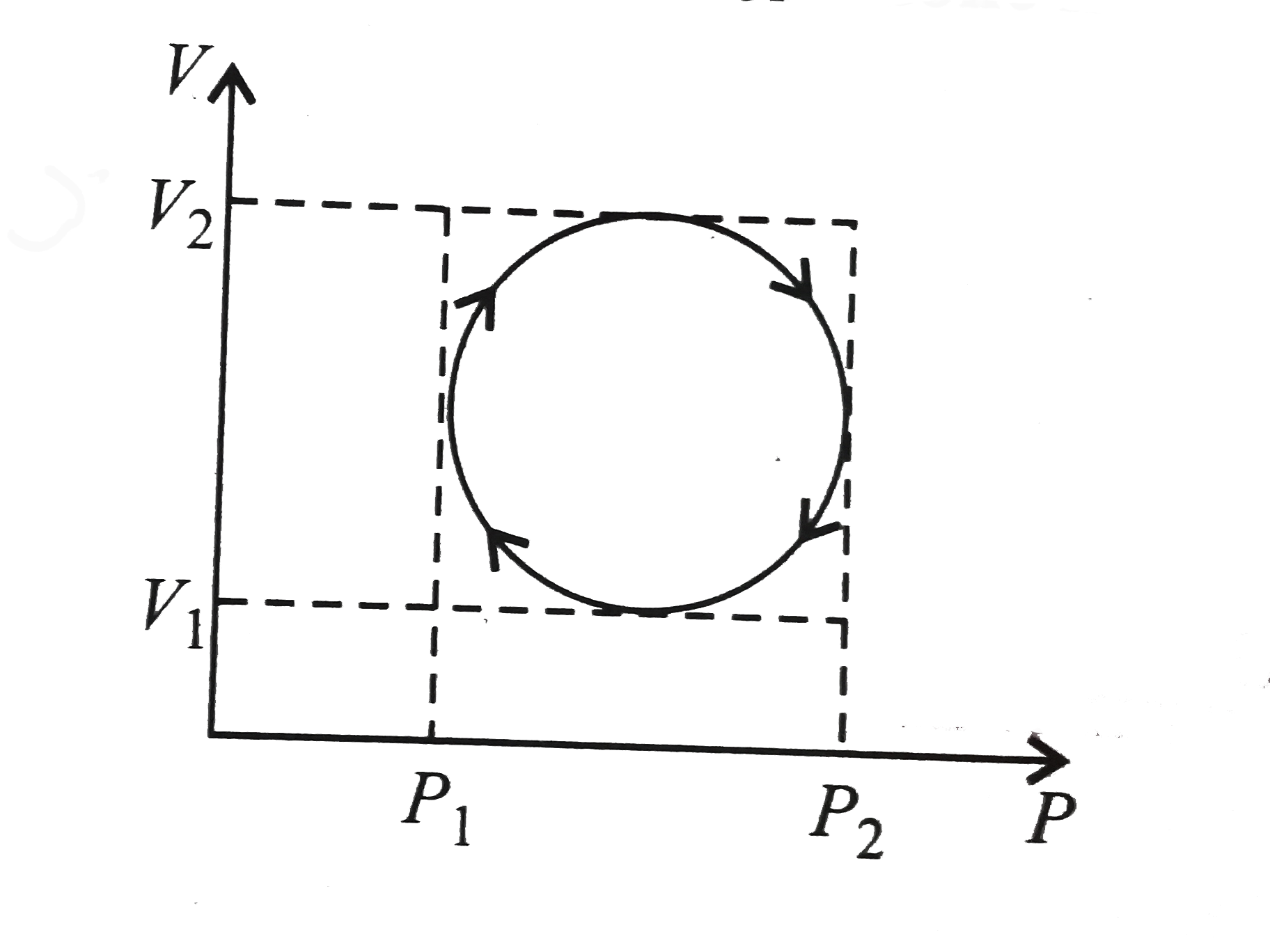
In a cyclic process shown on the P−V diargam the magnitude of the work done is :

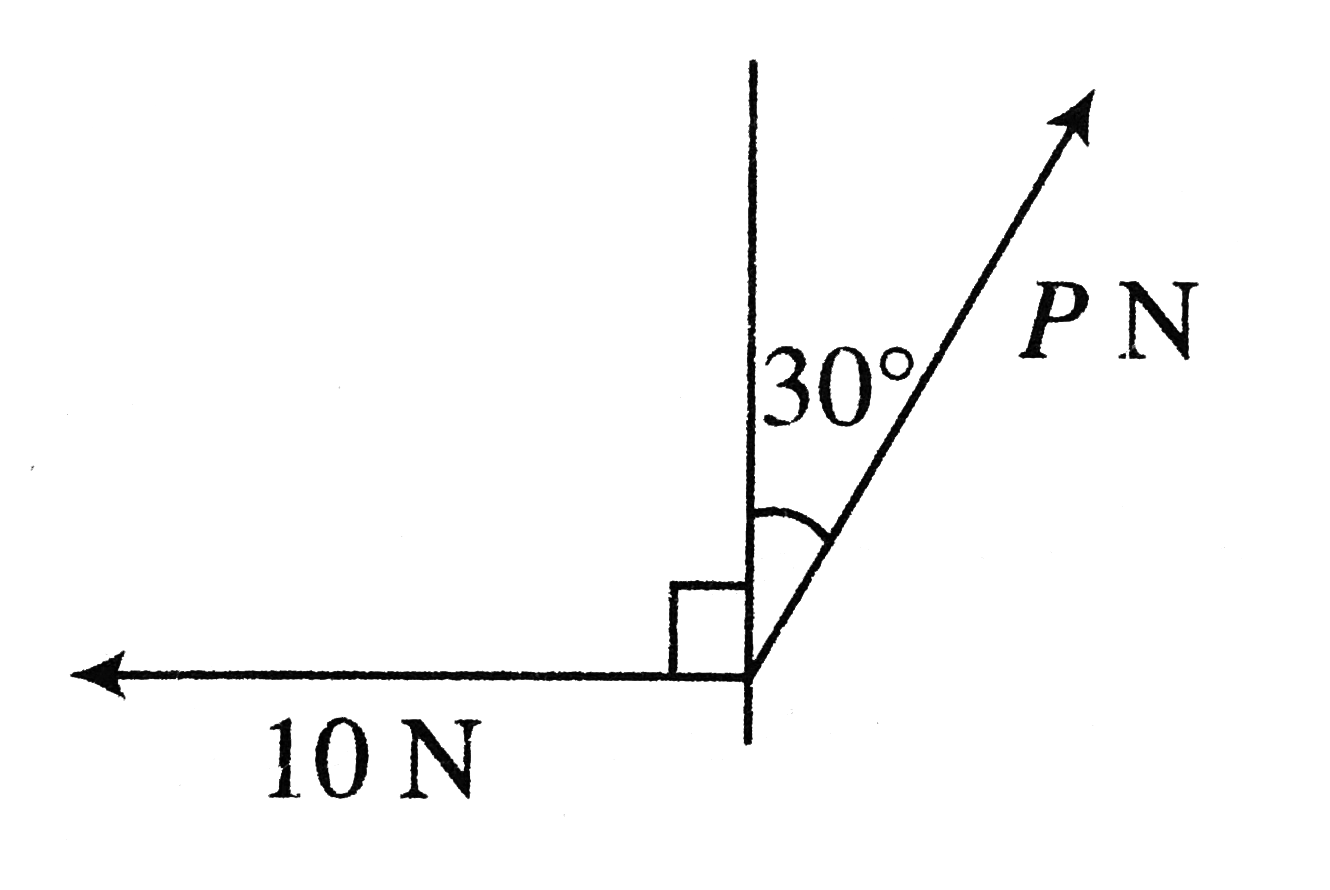
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionThe greatest & the least magnitude of the resultant of two forces of constant magnitudes are P & Q respectively. If the forces act at an angle 2α, then prove that the magnitude of their resultant is given by √P2cos2α+Q2sin2α.
View SolutionIn the cyclic process shown on V−P diagram, the magnitude of the work done is
View SolutionTwo forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
View Solution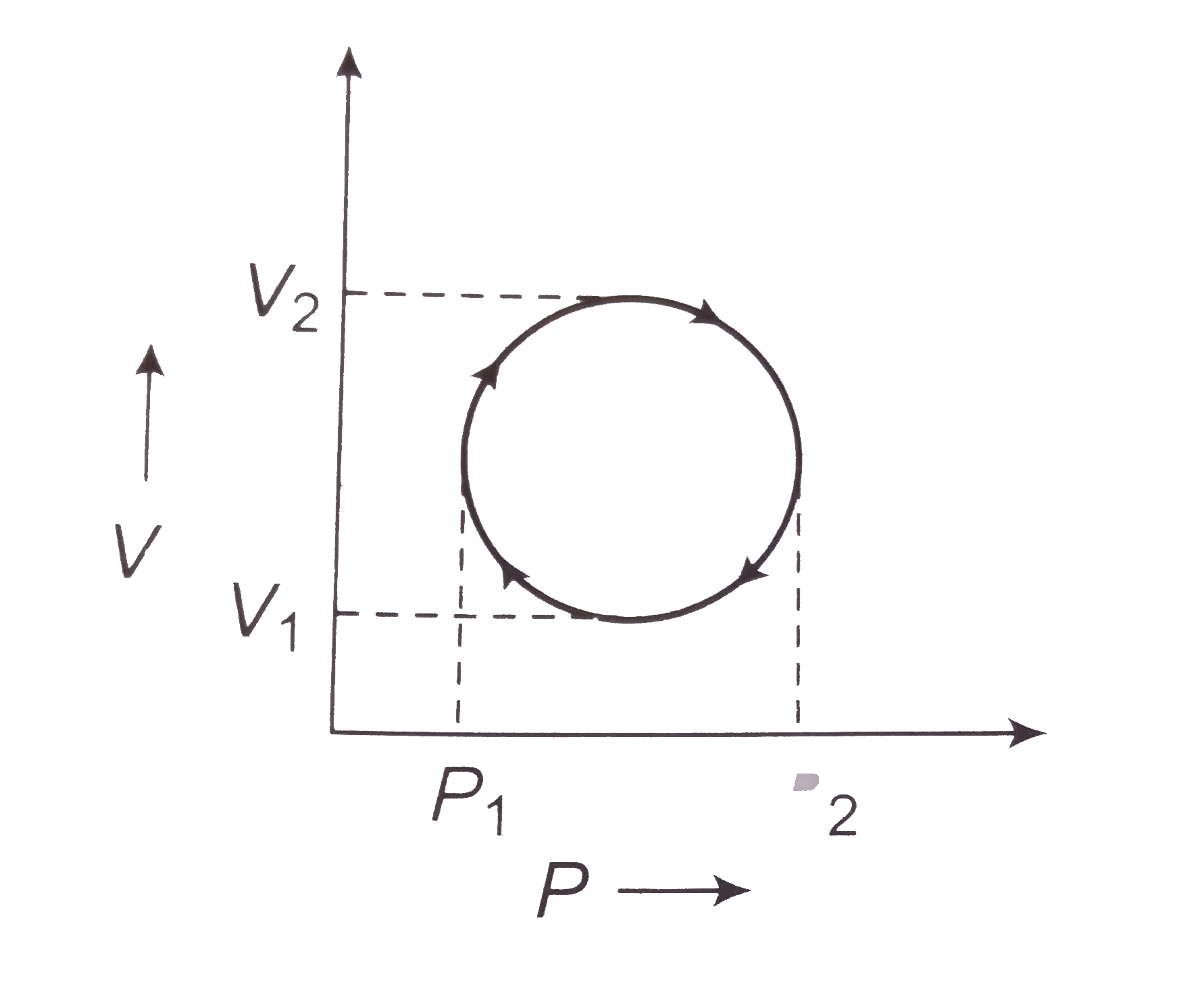
In the cyclic process shown in the V−P diagram the magnitude of the work is done is
View SolutionTwo forces whose magnitudes are in the ratio 3:5 give a resultant of 28N. If the angle of their inclination is 60∘, find the magnitude of each force.
View Solution