
In an elevator a system is arranged as shown in figure. Initially elevator is at rest and the system is in equilibrium with middle spring unstretched. When the elevator accelerated upwards, it was found that for the new equilibrium position (with respect to lift), the further extension i the top spring is 1.5 times that of the further compression in the bottom spring, irrespective of the value of acceleration
(a) Find the value of m1m2 in terms of spring constants for this happen.
(b) if k1=k2=k3=500Nm and m1=2 kg and acceleration of the elevator is 2.5ms2, find the tension in the middle spring in the final equilibrium with respect to lift.




Let the initial extension in top string be x1 and the compression in the botton string be x3 respectively.
For equilibrium of m1
k1x1o=m1g ..(1)
Forequilibriumofm_2<br>k_3x_3=m_2g..(2)<br>Letthee≤va→r⋆tsae≤rationwithanae≤rationa∈theupwarddirection.Now∈thepositionoff∈alequilibrium,≤tfurthercompression∈the⊥→mstr∈gbey.<br>Furtherextensionithe⊤str∈g=1.5y<br>and compression in the middle spring=0.5y IN the frame of lift
(a) m1(g+a)=k1(x1+1.5y)+k2(0.5y)
m1g=k1x1
m1a=y(32k1+12k2) ..(3)
m2(g+a)=k3(x3+y)−k2(0.5y)
m2g=k3x3
m2a=y(k3−k22) ..(4)
(3),(4)we≥t<br>(m_1)/(m_2)=(3k_1+k_2)/(2k_3-k_2)<br>(b)k_1=k_2=k_3=500(N)/(m)<br>m_1=2kg<br>a=2.5(m)/(s)<br>using(3)<br>y=(2xx2.5)/(2xx500)=(1)/(200)m=0.5cm<br>Tension∈them≤spr∈g=k(0.5y)<br>=500xx(1)/(2)xx(1)/(2)xx10^-2<br>T=1.25N
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - single correct type
14 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
Consider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
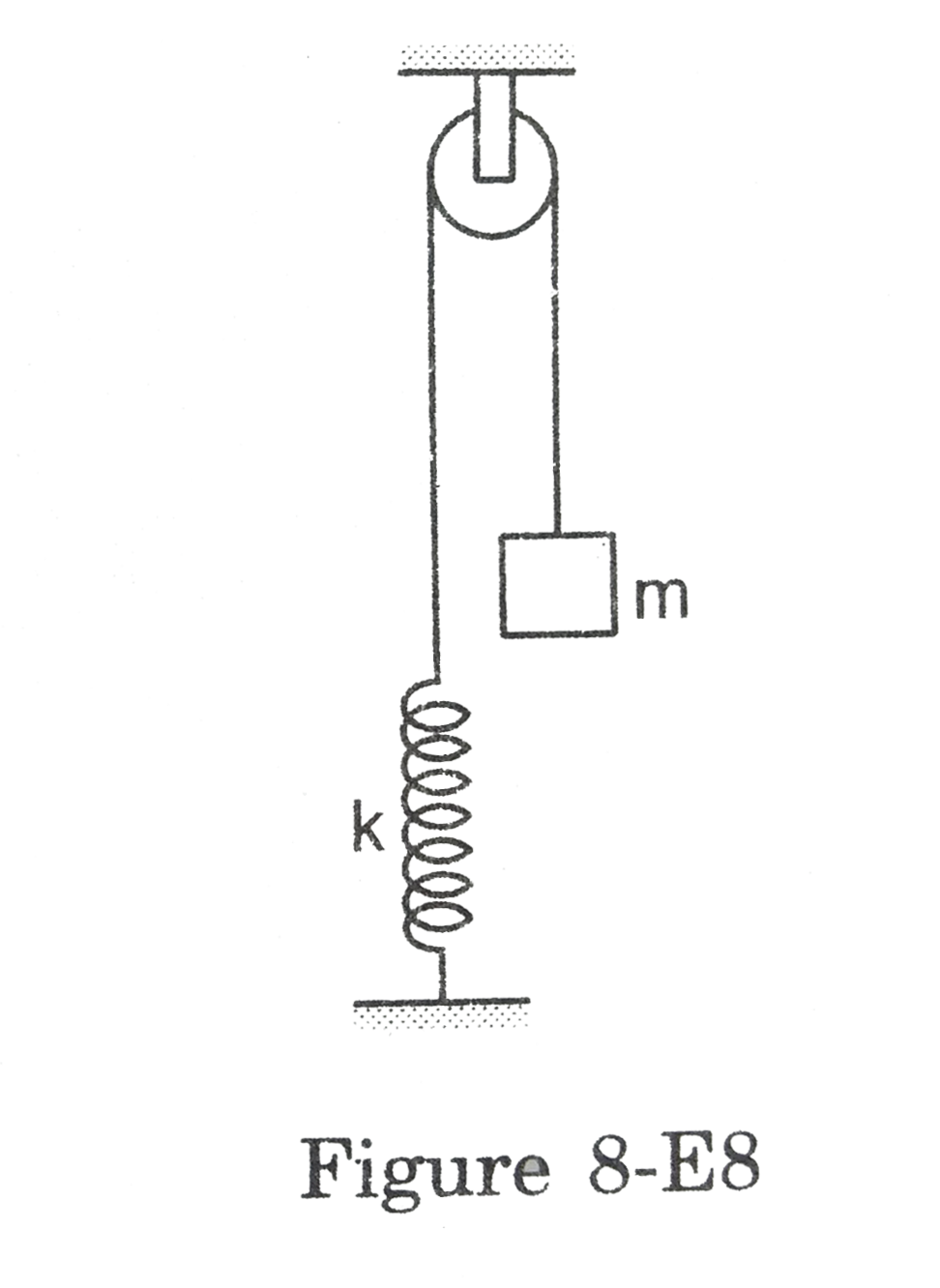
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
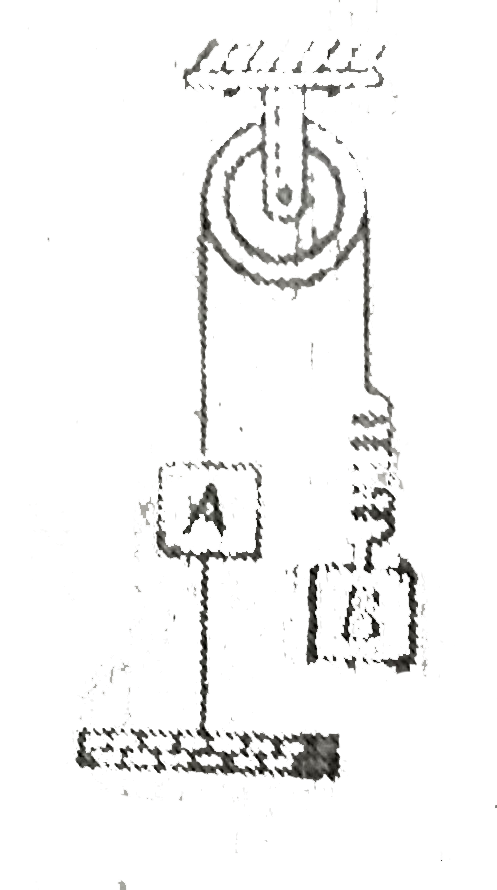
View Solution
Knowledge Check
All surfaces shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be
 Amg√2KB2mgkC(M+m)g√2kDmgk
Amg√2KB2mgkC(M+m)g√2kDmgkAll surfaces shown in figure are smooth. System is released with the spring instretched. In equilibrium, compression in the spring will be
 A2mgkB(M+m)g√2kCmg√2kDmgk
A2mgkB(M+m)g√2kCmg√2kDmgkIn the equilibrium conditions shown in the figure all the springs have unstretched length l
 Aspring constant of all the spring is sameBspring constant of third spring is maximumCspring force is minimum in second springDspring constant is maximum in fourth spring
Aspring constant of all the spring is sameBspring constant of third spring is maximumCspring force is minimum in second springDspring constant is maximum in fourth spring
If extension in the spring at equilibrium position is 6 cm then acceleration of block if it is released by further stretching 4 cm.
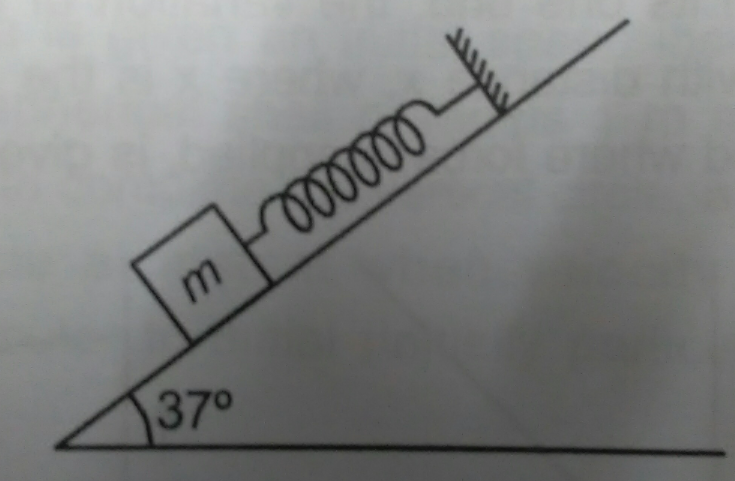
View SolutionIf extension in the spring at equilibrium position is 6 cm then acceleration of block if it is released by further stretching 4 cm.

View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
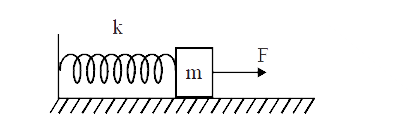
maximum extension in the spring
View SolutionIn an elevator, a spring clock of time period Ts (mass attached to a spring) and a pendulum clock of time period Tp are kept. If the elevator accelerates upwards
View SolutionIn an elevator, a spring clock of time period Ts (mass attached to a spring) and a pendulum clock of time period Tp are kept. If the elevator accelerates upwards
View Solution
