
Two blocks of mass M and 3M (in kg) are connected by an inextensible light thread which passes over a light frictionless pulley. The whole system is placed over a fixed horizontal table as shown.The coefficient of friction between the blocks and table surface is . The pulley is pulled by a string sttached to its centre and accelerated to left with acceleration . Assume that gravity acts with constant acceleration g downwards through the plane of table. Then:
(a) Find the forizontal accelration of both the blocks (Assume that both the blocks are moving.)
(b) What is the maximum acceleration a, for which the block of mass 3 M will remain stationary?


(a) Let the acceleration of blocks of mass M and 3 M are and respectively. From constraint relation
.(i)
F.B.D. of block of mass M
.(ii)
F.B.D. of block of mass 3 M
.(iii)
From (ii) and (iii):
From (i) and (iv)
From (i) and (v)
(b) Since
Acceleration a will be maximum when is maximum (since)
Acceleration is maximum when tension in the string is maximum for block of mass 3 M to be stationary
For block of mass M
So maximum acceleration
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - single correct type
14 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
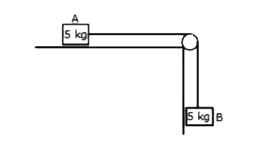
A block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and the surface is 0.5. Tension in the cord is (g=9.8m/s2 )
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
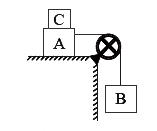
View Solution
Knowledge Check
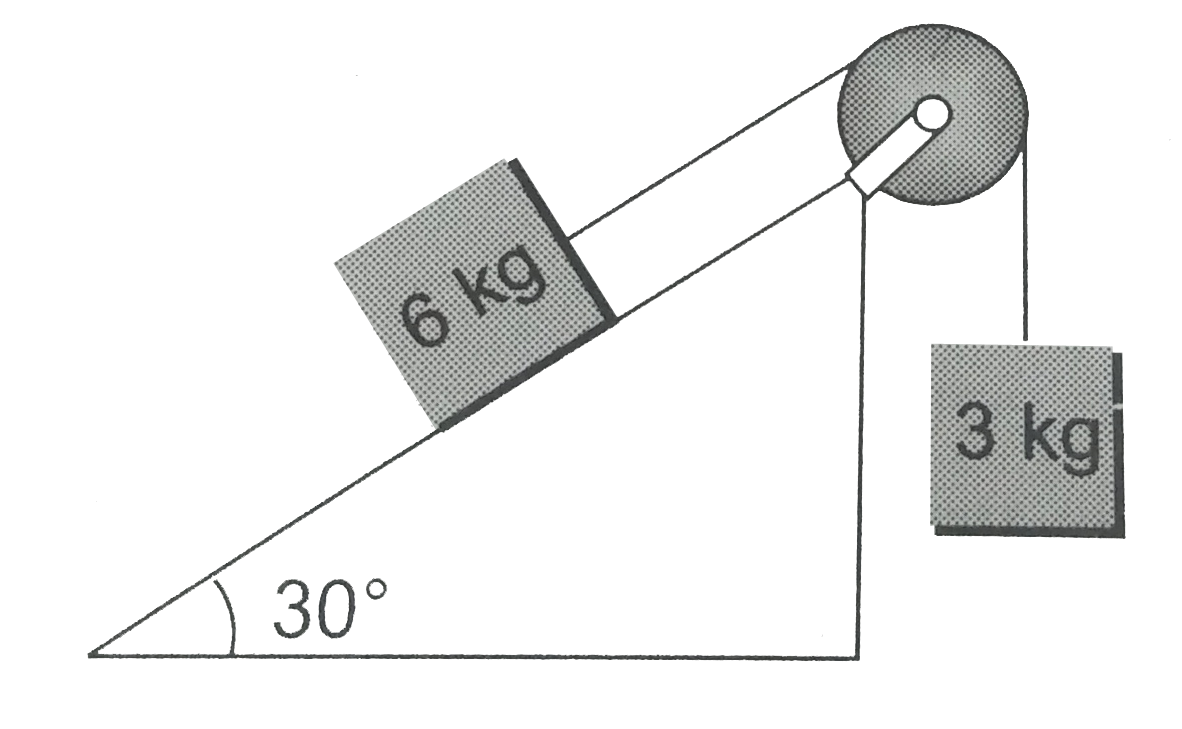
Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2Two masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A(m1−m2m1+m2)2gBm1−m2m1+m2gCm1+m2m1−m2gDZeroTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
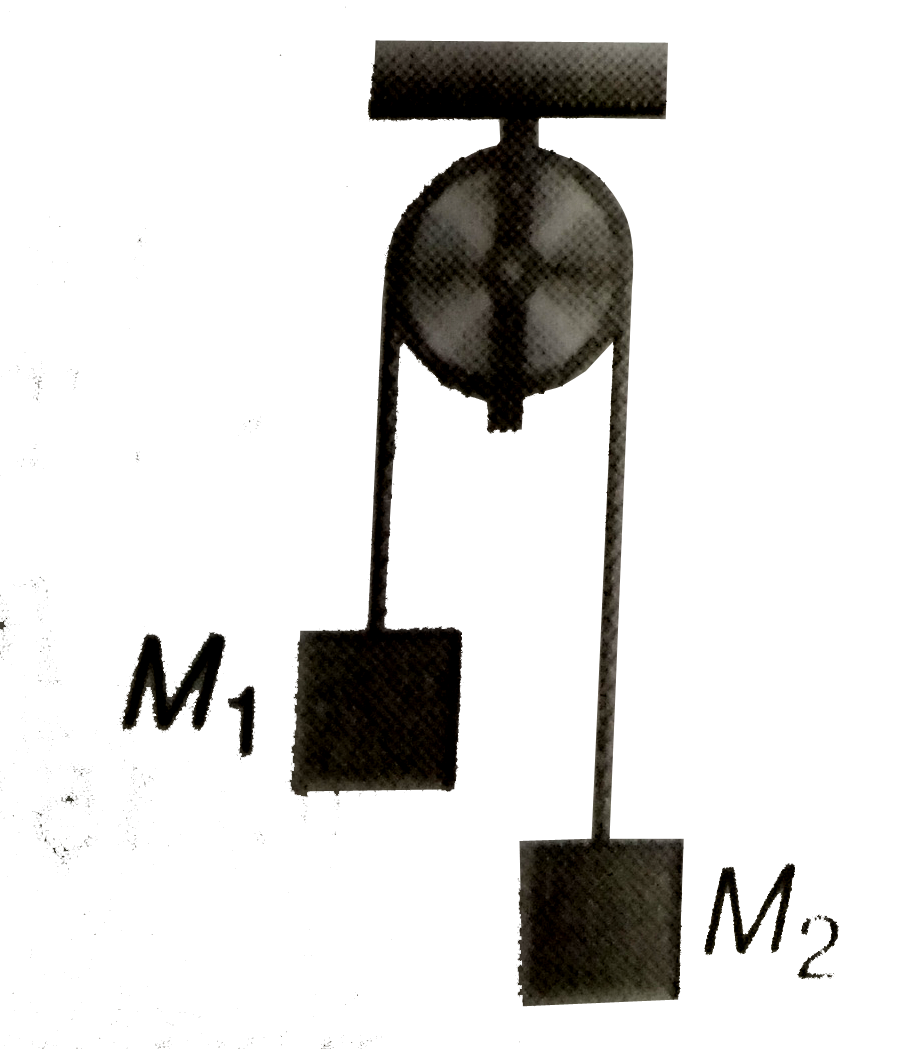 AgBg/2Cg/3Dg/4
AgBg/2Cg/3Dg/4
Two blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
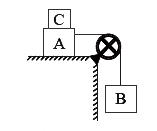
View SolutionOn the figure shown two blocks each of mass 2 kg are connected though a massless inextensible string, which posses over a frictionless pulley. The coefficient of friction between any two surface is μ=0.1. Find the acceleration of the blocks.
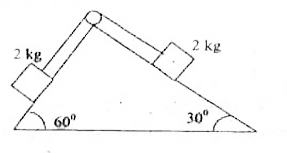
View SolutionOn the figure shown two blocks each of mass 2 kg are connected though a massless inextensible string, which posses over a frictionless pulley. The coefficient of friction between any two surface is μ=0.1. Find the acceleration of the blocks.

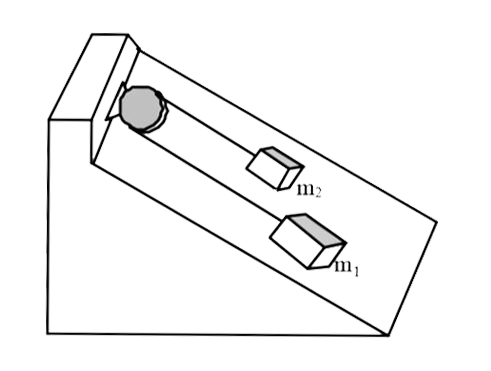
View SolutionTwo blocks on a rough incline are connected by a light string that passes over a frictionless light pulley as shown. Assuming m1>m2 and takingthe coefficient of kinetic friction for each block to be μ we get acceleration of the blocks as -
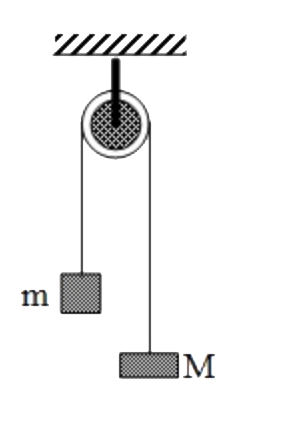
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
View Solution
