In an experiment for determining the value of acceleration due to gravity (g) using a simpe pendulum , the following observations were recorded:
Length of the string (l)=98.0cm
Diameter of the bob (d)=2.56cm
Time for 10oscillations(T)=20.0s
Calculate the value of g with maximum permissible absolute error and the percentage relative error.
The correct Answer is:(9.80±0.11)ms−2
Time period for a simple pendulum is T=2π√leffg …..(i)
where leff is the efective length of the pendulum equal to (l+d2) and time period equals T=20.010=2.00s
From (i) , we get g=4π2(_(eff))T2
To calculate actual value of g,
Since g=4π2(98+1.28)(2.00)2=980cms−2=9.80ms−2
Error int he value of g:
Δgg=Δleffleff+2(ΔTT)=Δl+Δrl+r+2(ΔTT)
Further , since errors can never exceed the least count of he measuring instrument. So , Δl=0.1cmandΔr=0.01cm.
Δgg=(0.1+0.0198.0+1.28)+2(0.120.0)
⇒=0.0011+0.01=0.0111
Thus , percentage error Δgg×100%=1.1%
and absolute error =Δg=g(0.011)=0.11ms−2
So , g=(9.80ms−2±1.1%)=(9.80±0.11)ms−2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Single Correct93videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.317videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
Similar Questions
To find the value of 'g' by using a simple pendulum, the following observations were made: Length of the thread, I=(100±0.1)cm Time period of oscillation, T=(2±0.1)s Calculate the maximum permissible in measurement of 'g' which quanitiy should be measured more accurately and why ?
View SolutionIn determination of value of acceleration due to gravity (g) by simple pendulum, the time period is measured by a topwatch (L.C. = 0.5 second) and length of the thread is measured with metre scale (L.C. 0.1 cm) and diametre of bob is measured with vernier callipers (L.C. = 0.1 cm). The following observations are recorded :
Length of the thread =105.3cm
Diameter of the bob =2.45cm
Time period =2.07s
Number of oscillations =10
Calculate the value of g, estimate error and write the result in proper significant figures.View Solution
Knowledge Check
- Question 1 - Select One
In an experiment of determine acceleration due to gravity by simple pendulum, a student commits 1% positive error in the measurement of length and 3% negative error in the time then % error in g will be
A3%B4%C7%D10% - Question 2 - Select One
Student I, II and III perform an experiment for measuring the acceleratioon due to gravity (g) using a simple pendulum . Theu use different lengths of the pedulum and /or record time for different number of oscillations . The observation are shoen in the table .
Least count for length =0.1cm
Least count for time =0.1s
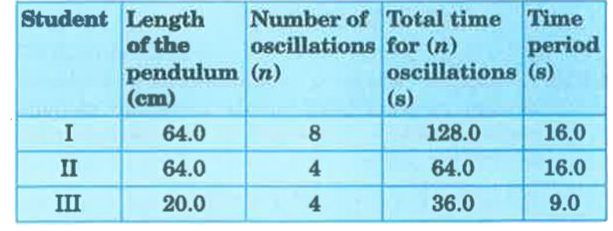
If EI, EIIand EIIIare the percentage errors in g,i.e
Δgg×100for students I, II, and III respectively ,AEI=0BEI is minimumCEI=EIIDEII is maximum - Question 3 - Select One
While measuring acceleration due to gravity by a simple pendulum , a student makes a positive error of 2% in the length of the pendulum and a positive error of 1% in the measurement of the value of g will be
A3%B0%C4%D5%
The value of acceleration due to gravity is 980cms−2. What will be its value if the unit of length is kilometer and that of time is minute?
View SolutionIn an experiment , the following observations were recorded:
L=2.820m,M=3.00kg,l=0.087cm,diameter,D=0.041cm. Taking g=9.81ms−2 and using the formula , Y=4MgLπD2l , find the maximum permissible error in Y.View SolutionThree students S1,S2andS3 perform an experiment for determining the acceleration due to gravity (g) using a simple pendulum. They use different lengths of pendulum and record time for different number of oscillations. The observations are as shown in the table.

(Least count of length = 0.1 m least count for time = 0.1 s)
If E1,E2andE3 are the percentage errors in 'g' for students 1, 2 and 3 respectively, then the minimum percentage error is obtained by student no._____.View SolutionAn experiment is performed to obtain the value of acceleration due to gravity g by using a simple pendulum of length L. In this experiment time for 100 oscillations is measured by using a watch of 1 second least count and the value is 90.0 seconds. The length L is measured by using a meter scale of least count 1 mm and the value is 20.0 cm. The error in the determination of g would be:
View SolutionIn an experiment to determine acceleration due to gravity, the length of the pendulum is measured as 98 cm be a scale of least count of 1 cm. The period of swing/oscillations is measured with the help of a stop watch having a least count of 1s. The time period of 50 oscillation is found to be 98 s. Express value of g with proper error limits.
View Solution

