In an experiment, two capacities measured are (1.3±0.1)μF and (2.4±0.2)μF. Calculate the total capacity in parallel with percentage error.
To solve the problem of calculating the total capacitance in parallel and the percentage error, we can follow these steps:
Step 1: Identify the given values
We have two capacitors:
- C1=1.3μF with an uncertainty of ΔC1=0.1μF
- C2=2.4μF with an uncertainty of ΔC2=0.2μF
Step 2: Calculate the total capacitance in parallel
When capacitors are connected in parallel, the total capacitance C is given by the sum of the individual capacitances:
C=C1+C2
Substituting the values:
C=1.3μF+2.4μF=3.7μF
Step 3: Calculate the total uncertainty in capacitance
The total uncertainty ΔC in the capacitance when adding two values is the sum of their individual uncertainties:
ΔC=ΔC1+ΔC2
Substituting the uncertainties:
ΔC=0.1μF+0.2μF=0.3μF
Step 4: Calculate the percentage error
The percentage error is calculated using the formula:
Percentage Error=(ΔCC)×100
Substituting the values we found:
Percentage Error=(0.3μF3.7μF)×100
Calculating this gives:
Percentage Error≈8.1%
Final Answer
The total capacitance in parallel is 3.7μF with a percentage error of approximately 8.1%.
---
We have two capacitors:
- C1=1.3μF with an uncertainty of ΔC1=0.1μF
- C2=2.4μF with an uncertainty of ΔC2=0.2μF
When capacitors are connected in parallel, the total capacitance C is given by the sum of the individual capacitances:
C=C1+C2
Substituting the values:
C=1.3μF+2.4μF=3.7μF
The total uncertainty ΔC in the capacitance when adding two values is the sum of their individual uncertainties:
ΔC=ΔC1+ΔC2
Substituting the uncertainties:
ΔC=0.1μF+0.2μF=0.3μF
The percentage error is calculated using the formula:
Percentage Error=(ΔCC)×100
Substituting the values we found:
Percentage Error=(0.3μF3.7μF)×100
Calculating this gives:
Percentage Error≈8.1%
The total capacitance in parallel is 3.7μF with a percentage error of approximately 8.1%.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Conceptual Problem
65 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - NCERT Exercises
40 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
Knowledge Check
In the given network capacitance, C1=10μF,C2=5μF and C3=4μF. What is the resultant capacitance between A and B?
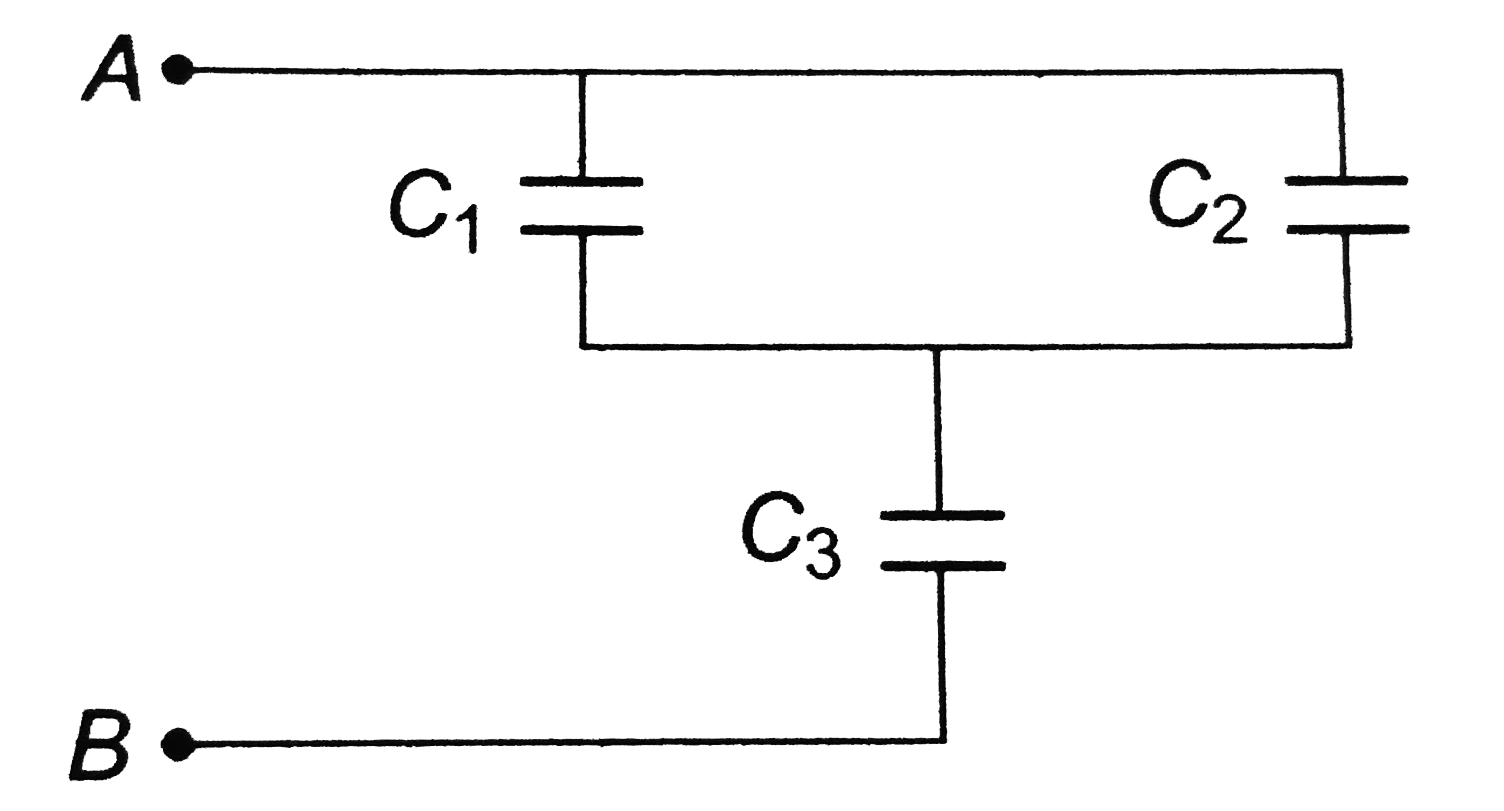 A2.2μFB3.2μFC1.2μFD4.7μF
A2.2μFB3.2μFC1.2μFD4.7μFTwo capacitors of capacitances 1μFand3μF are charged to the same voltages 5V. They are connected in parallel with oppositely charged plates connected together. Then
AFinal common voltage will be 5VBFinal common voltage will be 2.5CHeat produced in the circuit will be zeroDHeat produced in the circuit will be 37.5μJThe ratio of the resultant capacities when three capacitors of 2μF,4μFand6μF are connected first in series and then in parallel is
A1:11B11:1C12:1D1:12
The volumes of two bodies are measured to be
V1=(10.2±0.02)cm3andV2=(6.4±0.01)cm3. Calculate sum and difference in volumes with error limits.
View SolutionThree capacitances of capacity ,10 muF, 5 muF" and "5muF" are connected in parallel.The total capacity will be
View SolutionTwo resistances R1=(15±0.5)Ω and (20±0.7)Ω are connected in parallel. Calculate the total resistance of the combination and maximum percentage error.
View SolutionA physical quantity is measured as Q=(2.1±0.5) units. Calculate the percentage error in (1)Q2(2)2Q.
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat ( in mili joule ) generated when this capacitor is connected in parallel to n another capacitor of same capacity?
View Solution
