In an isobaric process, ΔQ=Kγγ−1 where γ=CP/CV. What is K?
Pressure
Volume
ΔU
ΔW
The correct Answer is:D
d. ΔQ=Kγγ−1=KCP/CV(CP/CV)−1=KCPCP−CV
=K(nCPΔT)(nCPΔT−nCvΔT)=KΔQ(ΔQ−ΔU)=KΔQΔW
or 1=KΔw⇒K=ΔW
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
Write the expressions for CvandCp of a gas in terms of gas constant R and γ where
γ=Cp/Cv
View SolutionA gas undergoes cyclic process 1-2-3-4-1 in which 1-2 and 3-4 are adiabatic process 2-3 and 4-1 are isobaric process. If P2P1=k then what will be the efficiency of cycle in terms of k and γ where γ=Cp/Cv.
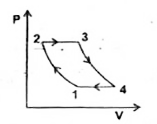
View Solution
Knowledge Check
For adiabatic processes (γ=CpCv)
APγV=constantBTγV=constantCTVγ−1=constantDTVγ=constantThe ratio γ(CPCV) for iner gases is
A1.33B1.66C2.13D1.99Read the passage and answer the following question.
It is known that the expansion of air follows adiabatic expansion. When sound waves propagate through the air velocity is given by √Pγρ where γ=CPCV. Assume you are in a planet where it is filled only with dry N2 and γ=1.4 and molar mass of N2=28. The temperature of the atmosphere is 300 K. The ideal gas equation PV = nRT is obeyed where P is pressure, v = volume, n = number of moles, T = temperature, R=8.314 J mol−1K−1.
What will be a suitable formula for velocity amongst the followingA√PρB√γnRTMC√γRTMD√γρ
Read the passage and answer the following question.
It is known that the expansion of air follows adiabatic expansion. When sound waves propagate through the air velocity is given by √Pγρ where γ=CPCV. Assume you are in a planet where it is filled only with dry N2 and γ=1.4 and molar mass of N2=28. The temperature of the atmosphere is 300 K. The ideal gas equation PV = nRT is obeyed where P is pressure, v = volume, n = number of moles, T = temperature, R=8.314 J mol−1K−1.
What will be the velocity in the planet?
View SolutionIn previous, Find the value of γ=CP/Cv:
View Solutionif R is the molar gas constant and γ=CP/CV, then CV is equal to
View SolutionIf R is the molar gas constant and γ=CP/CV, then Cp is equal to
View SolutionA gas expands adiabatically at constant pressure such that:
T∝1√V
The value of γ i.e., (CP/CV) of the gas will be:
View Solution
