In an LC circuit the capacitor has maximum charge q0. The value of (dIdt)max is

q0LC
q0√LC
q0LC−1
q0LC+1
The correct Answer is:A
(VC)max=(VL)max
q0C=L(dIdt)max
∴(dIdt)max=q0LC
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
In LC circuit the maximum charge in capacitor is q0. Then maximum value of rate of change of current is
View SolutionThe figure shows an RC circuit with a parallel plate capacitor. Before switching on the circuit, plate A of the capacitor has a charge. −Q0 while plate B has no net charge. If at t=0, the switch is closed then after how much time (in seconds) will the net charge on plate A becomes zero? [Given : C=1μF,Q0=1mC,ε=1000VandR=2×1061n3Ω]
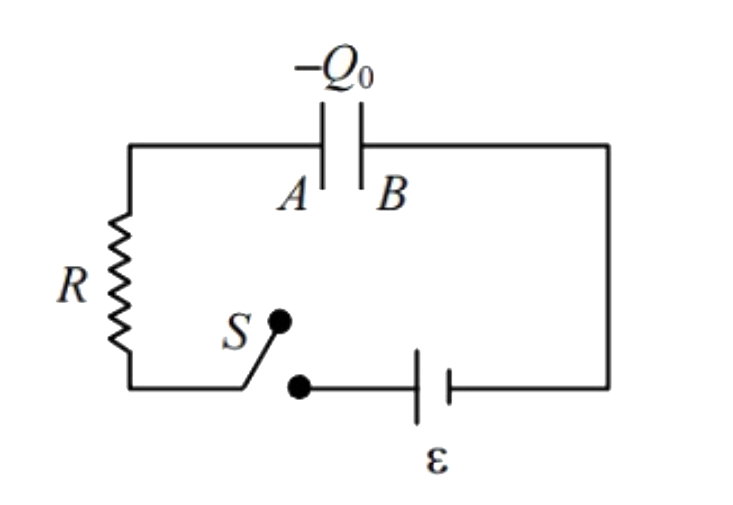
View Solution
Knowledge Check
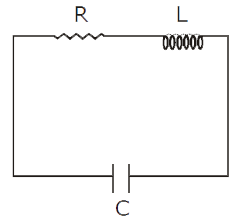
An LCR circuit is equivalent to a damped pendulum In an LCR circuit the capacitor is charged to Q0 and then connected to the L and R as shown below : Thus potential energy stored in the capacitor and that in the inductor also oscillates between maximum value an zero with double the frequency.
If a student plots graphs of the square of maximum charge (Q2max) on the capacitor with time (t) for two different values L1andL2(L1>L2) of L then which of the following reprersent this graph correctly ? (Plots are shematic and not drawn to scale )A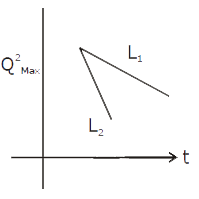 B
B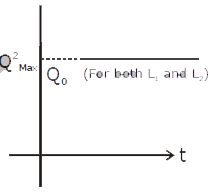 C
C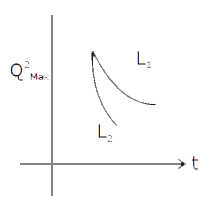 D
D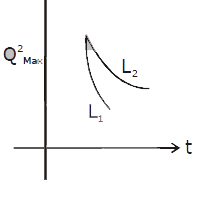
An LCR curcuit is equivalent to a damped pendulum. In an LCR circuit the capacitor is charged to (Q0) and then connected to the L ans R as shown below.

If a student plaots graphs of the square of maximum charge (Q2max) on the capacitor with time (t) for two different values L1andL2(L1>L2) of L then which of the following represents this graph correclty? (plots are schematic and not drawn to scale).A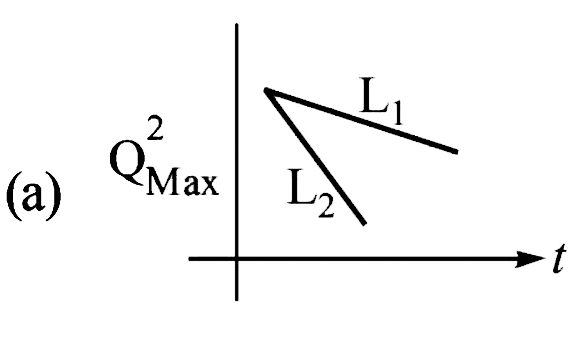 B
B C
C D
D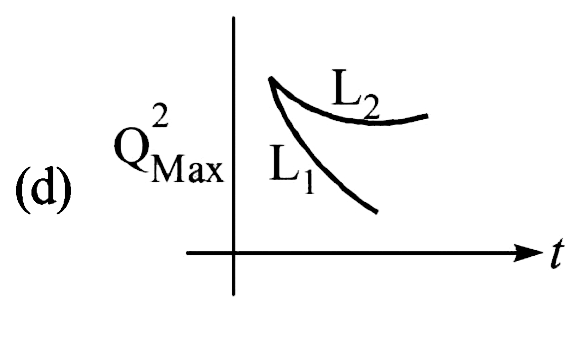
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
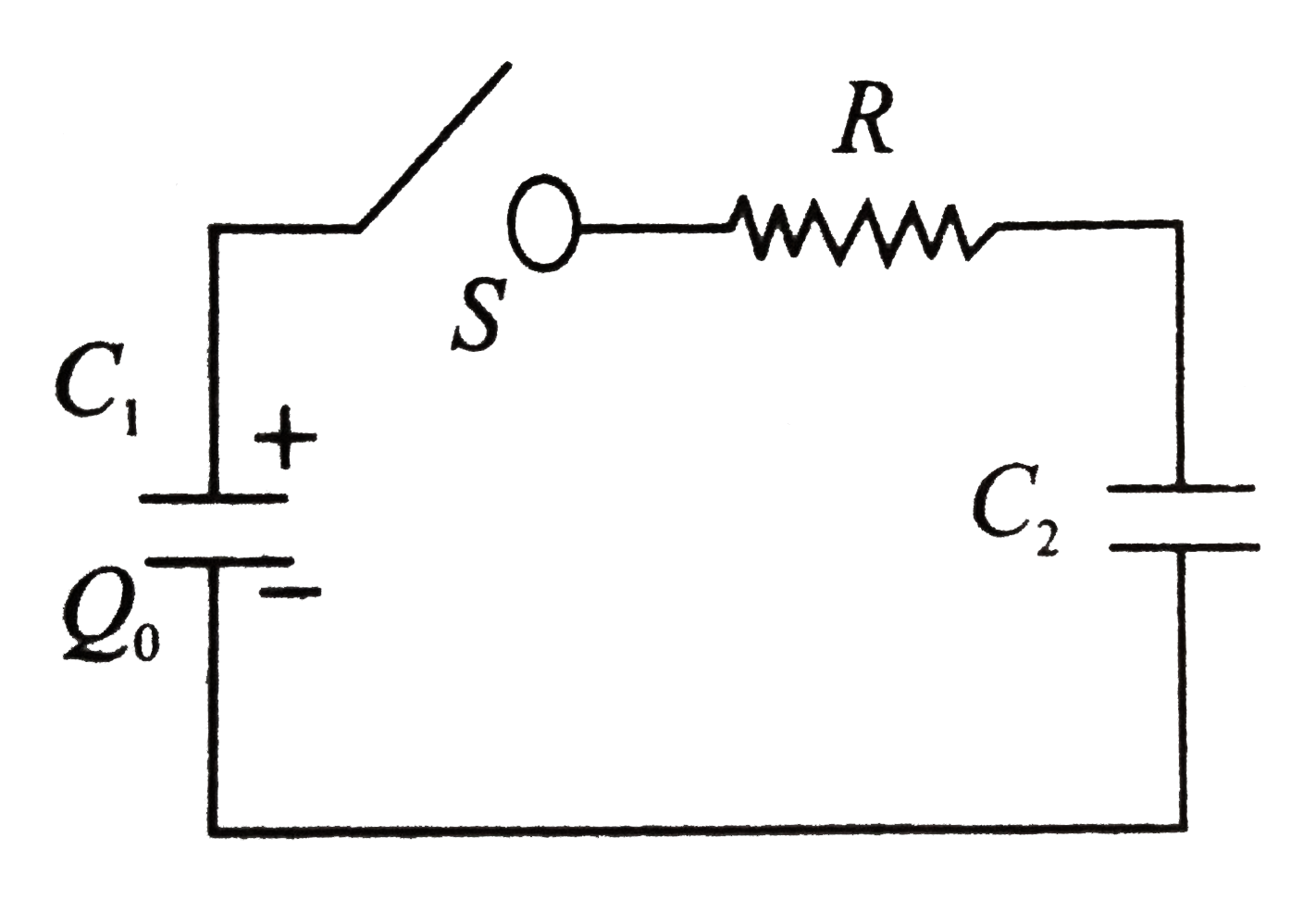 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
An LC circuit oscillating at natural frequency conssts of an inductor of inductance 30 m H and a capacitor of capacitance 60μF. The maximum value of instantaneous charge on capacitor in the circuit is 200 μC . If I is the current in the circuit then answer the following :
(i) What is the value of dIdt when charge is 150 μC?
(ii) Calculate the value of I when charge is 200 μC .
(iii) Find the maximum value of I.
(iv) For what value of q I is half of its maximum value ?
View SolutionThe frequency of oscillation of a certain LC circuit is 200 kHz. At time t = 0, plate A of the capacitor has maximum positive charge. At what earliest time t > 0 will (a) plate A again have maximum positive charge, (b) the other plate of the capacitor have maximum positive charge, and (c) the inductor have maximum magnetic field?
View SolutionR-C Circuit||Charging of Capacitor
View SolutionIn the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0
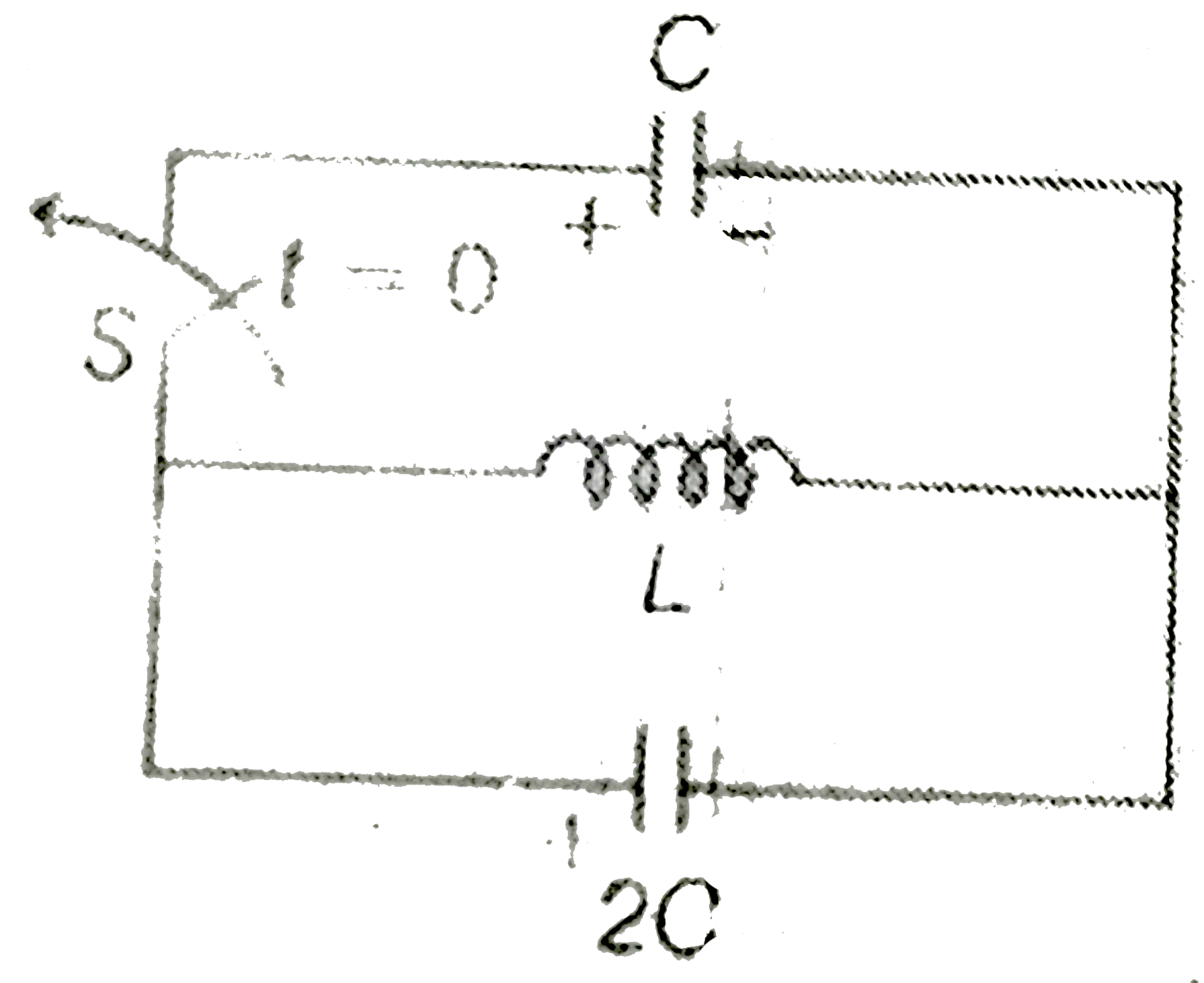
View SolutionA 8μHinductor is shorted across a 2μF capacitor. The capacitor is initially charged to 20 V. The maximum value of the current in the circuit is
View Solution
