In an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
Q2
Q√3
Q√2
Q
The correct Answer is:C
To solve the problem, we need to determine the charge on the capacitor when the energy is equally distributed between the electric field and the magnetic field in an oscillating LC circuit.
1. Understand the Energy in the LC Circuit:
The total energy U in an LC circuit is given by the formula:
U=12Q2/C
where Q is the maximum charge on the capacitor and C is the capacitance.
2. Condition for Equal Energy Distribution:
When the energy is equally distributed between the electric field and the magnetic field, each field will have half of the total energy:
Uelectric=Umagnetic=U2
3. Energy in the Electric Field:
The energy stored in the electric field when the charge on the capacitor is Q′ is:
Uelectric=12(Q′)2C
4. Energy in the Magnetic Field:
The energy stored in the magnetic field when the current is maximum (which occurs when the capacitor is half charged) is given by:
Umagnetic=12LI2
At the point where the energy is equally distributed, we can relate the current I to the charge Q′ on the capacitor. The current can be expressed in terms of charge as:
I=−dQdt
At the point of equal energy distribution, the charge on the capacitor will be such that:
Uelectric=Umagnetic
5. Setting Up the Equation:
Since both energies are equal, we can set them equal to each other:
12(Q′)2C=12LI2
However, we know that when the energy is equally distributed, the charge Q′ can be expressed as:
Q′=Q√2
6. Final Charge Calculation:
Therefore, the charge on the capacitor when the energy is equally distributed between the electric and magnetic fields is:
Q′=Q√2
Conclusion:
The charge on the capacitor when the energy is stored equally between the electric and magnetic fields is Q√2.
The total energy U in an LC circuit is given by the formula:
U=12Q2/C
where Q is the maximum charge on the capacitor and C is the capacitance.
When the energy is equally distributed between the electric field and the magnetic field, each field will have half of the total energy:
Uelectric=Umagnetic=U2
The energy stored in the electric field when the charge on the capacitor is Q′ is:
Uelectric=12(Q′)2C
The energy stored in the magnetic field when the current is maximum (which occurs when the capacitor is half charged) is given by:
Umagnetic=12LI2
At the point where the energy is equally distributed, we can relate the current I to the charge Q′ on the capacitor. The current can be expressed in terms of charge as:
I=−dQdt
At the point of equal energy distribution, the charge on the capacitor will be such that:
Uelectric=Umagnetic
Since both energies are equal, we can set them equal to each other:
12(Q′)2C=12LI2
However, we know that when the energy is equally distributed, the charge Q′ can be expressed as:
Q′=Q√2
Therefore, the charge on the capacitor when the energy is equally distributed between the electric and magnetic fields is:
Q′=Q√2
The charge on the capacitor when the energy is stored equally between the electric and magnetic fields is Q√2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
AQ2BQ√3CQ√2DQIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
AQ/2BQ/√3CQ/√2DQIn a charged capacitor the energy is stored in
Apositive chargeBboth in positive and negative chargeCthe electric field between the platesDthe edges of the capacitor plates
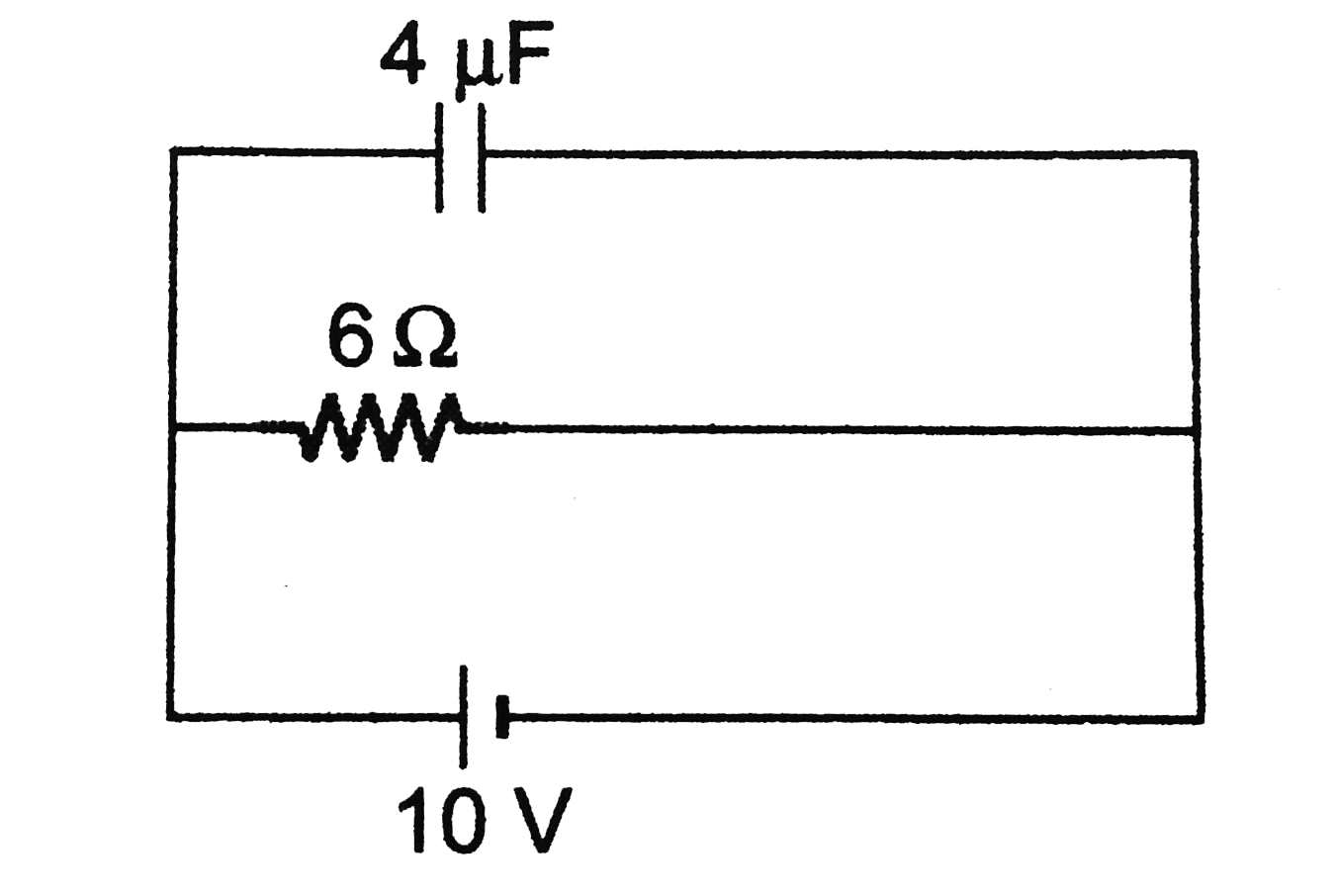
Find the charge stored in the capacitor.
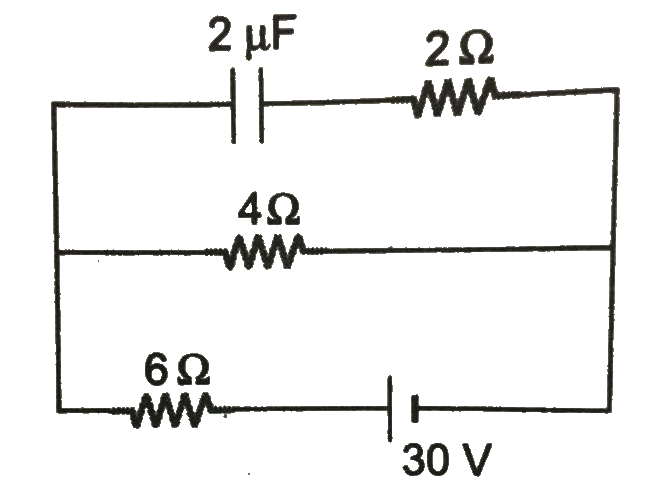
View SolutionFind the charge stored in the capacitor.
View SolutionWhat is the capacitance of an oscillating LC circuit if the maximum charge on the capacitor is 1.60 μC and the total energy is 140 μJ?
View SolutionIn LC circuit the maximum charge in capacitor is q0. Then maximum value of rate of change of current is
View SolutionIn a charged capacitor, the energy is stored in
View Solution