In an X - ray tube , electrons emitted from a filament (cathode) carrying current hit a target (anode) at a distance d form the cathode. The target is kept at a potential V higher than the cathode resulting in emission of continuous of and charateristic X - rays. It the filament current I is decreased to I2 , the potential difference V is increaed to 2v, and the separation distance d is reduuced to d2 ,then
The cut off wavelenghth will reduced to half, and the wavelenghts of the characteristi c X - rays wil reminan the same
the cut - off wavelength as well as the wavelenght of the characteristic X - rays will remain the same
the cut -off wavelenght will reduced to half , and the intensities of all the X - rays wil decrease
the cut - off wavelength will become two time larger, and the intensity of all the X -rays wil decrease
The correct Answer is:A,C
To solve the problem regarding the changes in an X-ray tube when certain parameters are altered, we will analyze the effects of these changes step-by-step.
Step 1: Understanding the Initial Conditions
In an X-ray tube, electrons are emitted from a cathode (filament) and accelerated towards an anode (target) due to a potential difference V. The kinetic energy gained by the electrons is converted into X-rays upon collision with the anode.
Step 2: Determine the Cut-off Wavelength
The cut-off wavelength λcut−off is related to the maximum energy of the electrons, which can be expressed as:
Emax=eV
where e is the charge of the electron and V is the potential difference. The energy of the X-ray photon is also given by:
E=hcλ
where h is Planck's constant and c is the speed of light. Setting these equal gives:
λcut−off=hceV
This shows that the cut-off wavelength is inversely proportional to the potential V.
Step 3: Analyze the Changes
1. Filament Current Decrease: The filament current I is decreased to I2. This affects the number of electrons emitted but does not directly affect the cut-off wavelength.
2. Potential Increase: The potential V is increased to 2V. Since the cut-off wavelength is inversely proportional to the potential, we have:
λ′cut−off=hce(2V)=12⋅hceV=12λcut−off
Thus, the cut-off wavelength is reduced to half.
3. Distance Decrease: The separation distance d is reduced to d2. This does not directly affect the cut-off wavelength or the energy of the emitted X-rays.
Step 4: Characteristic X-ray Wavelength
The wavelength of characteristic X-rays depends on the atomic number Z of the target material. Since the material of the anode is unchanged, the characteristic X-ray wavelength remains the same.
Step 5: Intensity of X-rays
The intensity of the emitted X-rays is proportional to the number of electrons hitting the anode. Since the filament current is decreased, the number of emitted electrons will also decrease, leading to a decrease in the intensity of the X-rays.
Conclusion
Based on the analysis:
- The cut-off wavelength is reduced to half.
- The wavelength of characteristic X-rays remains the same.
- The intensity of all X-rays decreases due to the reduced filament current.
Final Answer
The correct options are:
1. The cut-off wavelength will reduce to half and the wavelength of the characteristic X-ray will remain the same.
3. The cut-off wavelength will reduce to half and the intensity of all the X-rays will decrease.
In an X-ray tube, electrons are emitted from a cathode (filament) and accelerated towards an anode (target) due to a potential difference V. The kinetic energy gained by the electrons is converted into X-rays upon collision with the anode.
The cut-off wavelength λcut−off is related to the maximum energy of the electrons, which can be expressed as:
Emax=eV
where e is the charge of the electron and V is the potential difference. The energy of the X-ray photon is also given by:
E=hcλ
where h is Planck's constant and c is the speed of light. Setting these equal gives:
λcut−off=hceV
This shows that the cut-off wavelength is inversely proportional to the potential V.
1. Filament Current Decrease: The filament current I is decreased to I2. This affects the number of electrons emitted but does not directly affect the cut-off wavelength.
2. Potential Increase: The potential V is increased to 2V. Since the cut-off wavelength is inversely proportional to the potential, we have:
λ′cut−off=hce(2V)=12⋅hceV=12λcut−off
Thus, the cut-off wavelength is reduced to half.
The wavelength of characteristic X-rays depends on the atomic number Z of the target material. Since the material of the anode is unchanged, the characteristic X-ray wavelength remains the same.
The intensity of the emitted X-rays is proportional to the number of electrons hitting the anode. Since the filament current is decreased, the number of emitted electrons will also decrease, leading to a decrease in the intensity of the X-rays.
Based on the analysis:
- The cut-off wavelength is reduced to half.
- The wavelength of characteristic X-rays remains the same.
- The intensity of all X-rays decreases due to the reduced filament current.
The correct options are:
1. The cut-off wavelength will reduce to half and the wavelength of the characteristic X-ray will remain the same.
3. The cut-off wavelength will reduce to half and the intensity of all the X-rays will decrease.
Topper's Solved these Questions
- JEE (ADVANCE) 2020Book:JEE ADVANCED PREVIOUS YEARChapter:JEE (ADVANCE) 2020Exercise:SECTION 3
Explore 6 Videos
- JEE (ADVANCE) 2020Book:JEE ADVANCED PREVIOUS YEARChapter:JEE (ADVANCE) 2020Exercise:SECTION 3
Explore 6 Videos
- JEE ADVANCEDBook:JEE ADVANCED PREVIOUS YEARChapter:JEE ADVANCEDExercise:PHYSICS SECTION - IV Matrix Match Type
Explore 2 Videos
Similar Questions
Knowledge Check
if the cathode and the anode are kept at the same potential, the emitted electrons have
Athe same KE equal to 1.36 eVBthe average KE equal to (1.362) eVCthe maximum KE equal to 1.36 eVDthe minimum KE equal to 1.36 eVIf the potential difference between the anode and cathode of the X-ray tube is increases
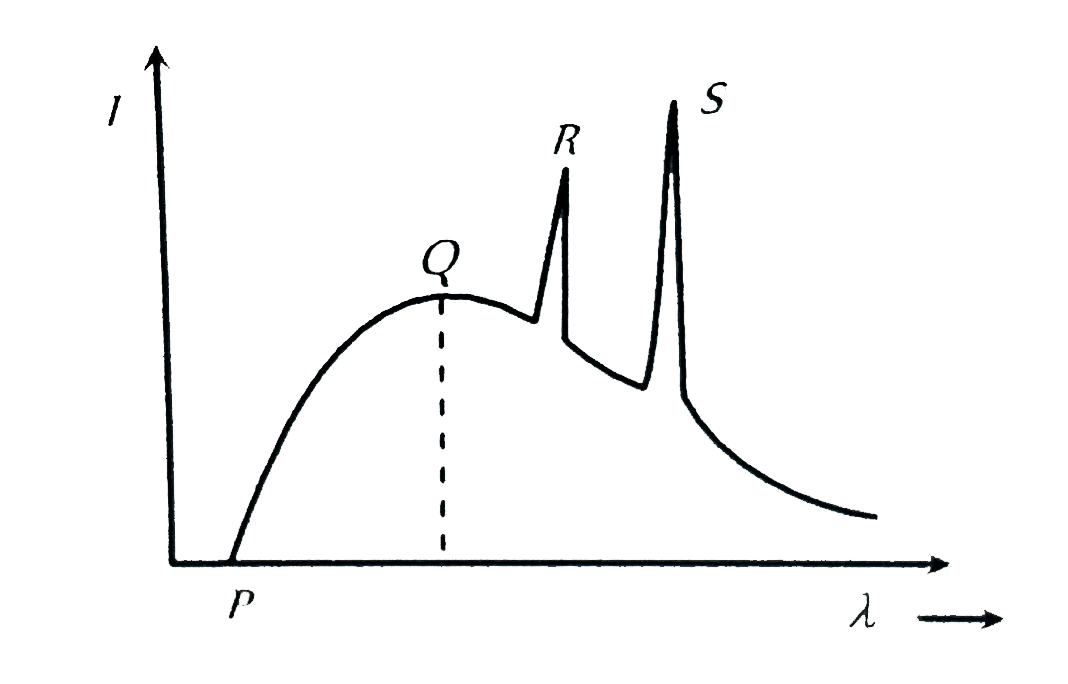 AThe peaks at R and S would move to shorter wavelengthBThe peaks at R and S would remain at the same wavelengthCThe cut off wavelength at P would decreaseD(b) and (c) both are correct
AThe peaks at R and S would move to shorter wavelengthBThe peaks at R and S would remain at the same wavelengthCThe cut off wavelength at P would decreaseD(b) and (c) both are correctCathode rays are
AElectromagnetic wavesBRadiationsCStream of α-particlesDStream of electrons.
Given two point of difference between cathode rays and anode rays
View SolutionCathode rays are
View SolutionThe binding energy of the innermost electron in tungsten is 40keV. To produce characteristic X - rays using a tungsten target in an X - rays tube the potential difference V between the cathode and the anti - cathode should be
View SolutionX-ray of wavelength λ=2 Å is emitted from the metal target. The potential difference applied across the cathode and the metal target is
View SolutionIf the potential difference between the anode and cathode of the X - ray tube is increases

View Solution
