A student skates up a ramp that makes an angle 30∘ with the horizontal . He/she starts ( as shown in the figure) at the bottom of the ramp with speed v0 and wants to turn around over a semicicular path xyz of radius R during which he/she reaches a maximum height h (at point ) form the ground as shown in the figure . Assume that the energy loss is negligble and the force required for this turn at the highest point is provided by his / her weight only. Then (g is the acceleration due to gravity).
v20−2gh=12gR
v20−2gh=√32gR
the centripetal force required at points x and z is zero
the centripetal force required is maximum at points x and z
The correct Answer is:A,D
To solve the problem, we will analyze the situation step by step:
Step 1: Understand the Energy Conservation
The student starts at the bottom of the ramp with speed v0 and moves up to point y at height h. We can use the principle of conservation of mechanical energy since energy loss is negligible.
Energy at the bottom (initial):
- Kinetic Energy (KE) = 12mv20
- Potential Energy (PE) = 0 (taking the bottom as the reference point)
Energy at point y (final):
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) = mgh
According to the conservation of energy:
Total Energy at bottom=Total Energy at point y
12mv20=mgh+12mv2
Step 2: Simplify the Equation
We can cancel m from both sides since it appears in all terms:
12v20=gh+12v2
Step 3: Rearranging the Equation
Rearranging gives us:
12v20−gh=12v2
Multiplying through by 2:
v20−2gh=v2
Step 4: Relate to Centripetal Force
At the highest point y, the only force providing the centripetal force is the weight of the student. The centripetal force Fc required for circular motion is given by:
Fc=mv2R
At the highest point, this centripetal force is provided by the weight:
mg=mv2R
Cancelling m gives:
g=v2R
Step 5: Substitute v2 from Energy Conservation
From our earlier equation, we have v2=v20−2gh. Substituting this into the centripetal force equation:
g=v20−2ghR
Rearranging gives:
gR=v20−2gh
Thus:
v20=gR+2gh
Step 6: Final Result
Now we can express the maximum height h in terms of v0 and g:
v20=g(R+2h)
This implies:
h=v202g−R2
The student starts at the bottom of the ramp with speed v0 and moves up to point y at height h. We can use the principle of conservation of mechanical energy since energy loss is negligible.
- Kinetic Energy (KE) = 12mv20
- Potential Energy (PE) = 0 (taking the bottom as the reference point)
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) = mgh
Total Energy at bottom=Total Energy at point y
12mv20=mgh+12mv2
We can cancel m from both sides since it appears in all terms:
12v20=gh+12v2
Rearranging gives us:
12v20−gh=12v2
Multiplying through by 2:
v20−2gh=v2
At the highest point y, the only force providing the centripetal force is the weight of the student. The centripetal force Fc required for circular motion is given by:
Fc=mv2R
At the highest point, this centripetal force is provided by the weight:
mg=mv2R
Cancelling m gives:
g=v2R
From our earlier equation, we have v2=v20−2gh. Substituting this into the centripetal force equation:
g=v20−2ghR
Rearranging gives:
gR=v20−2gh
Thus:
v20=gR+2gh
Now we can express the maximum height h in terms of v0 and g:
v20=g(R+2h)
This implies:
h=v202g−R2
Topper's Solved these Questions
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE (ADVANCE) 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 3
6 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PHYSICS SECTION - IV Matrix Match Type
2 Videos
Similar Questions
A spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
View SolutionA spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For a<<R the magnitude of the work done in the process is given by (4πpoRa2)X. where X is a a constant and y=Cp/Cv=41/30. The value of X is
View SolutionOne mole of a monatomic ideal gas is taken through a cycle ABCDA as shown in the P-V diagram. Column II gives the characteristics involved in the cycle. Match them with each of the processes given in Column I.

View SolutionA person in a wheelchair is moving up a ramp at constant speed.Their total weight is 900N. The ramp makes an angle of 37∘ with the horizontal. Calculate the component of its weight parallel and perpendicular to ramp.

View SolutionUniform ring of radius R is moving on a horizontal surface with speed v and then climbs up a ramp of inclination 30^(@) to a height h. There is no slipping in the entire motion. Then h is
View SolutionIn the picture shown, a ball standing from rest rolls down a ramp AB,goes along at the horizontal bottom BC, and then backs up a smaller ramp CD, thereafter rolls on horizontal plance DE Ignore friction and air resistance. Which of the following figure shows variation in speed with time?
View SolutionA box is projected up a long ramp (incline angle with the horizontal=30∘) with an initial speed of 8m/s. if the surface of the ramp is very smooth (essentially frictionless), how high up the ramp will the box go? What distance along the ramp will it slide?
View SolutionTwo ramp (1) and (2) are initially just touching each other and placed on a smooth horizontal surface A block released from the top of ramp (1) when it reaches to the other ramp (2) then the height attained by the block is -
View SolutionDanielle is a civil enginner for Dastis Dynamic Construction, Inc. She must create blueprints for a wheelchair accessible ramp leading up to the entrance of a mall that she and her group are building. The ramp must be exactly 100 meters in length and make a 20∘ angle with the level ground. What is the horizontal distance, in meters, from the start of the ramp to the point level with the start of the ramp immediately below the entrance of the mall, rounded to the nearest meter? (Disregard units when inputting your answer)
View SolutionAs shown above, a 10 - foot ramp forms an angle of 23∘ with the ground, which is horizontal. Which of the following is an expression for the vertical rise, in feet, of the ramp?
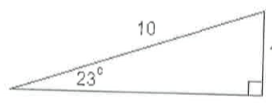
View Solution
The figure above shows a 14 - foot ramp that forms an angle of 63∘ with the vertical wall it is leaning against. Which of the following is an expression for the horizontal length, in feet, of the ramp?
View SolutionWhen condstructing wheelchair remps, the ramp must not rise more than 1 inch for every foot of ramp. What is the maximum angle the ramp can make with the ground for a 3 foot ramp ?
View SolutionAs shown in the figure below , with angles as marked ,a ramp is being designed that will have a vertical height of 4 feet . Which of the following is closest to the horizontal length of the ramp , in feet ?
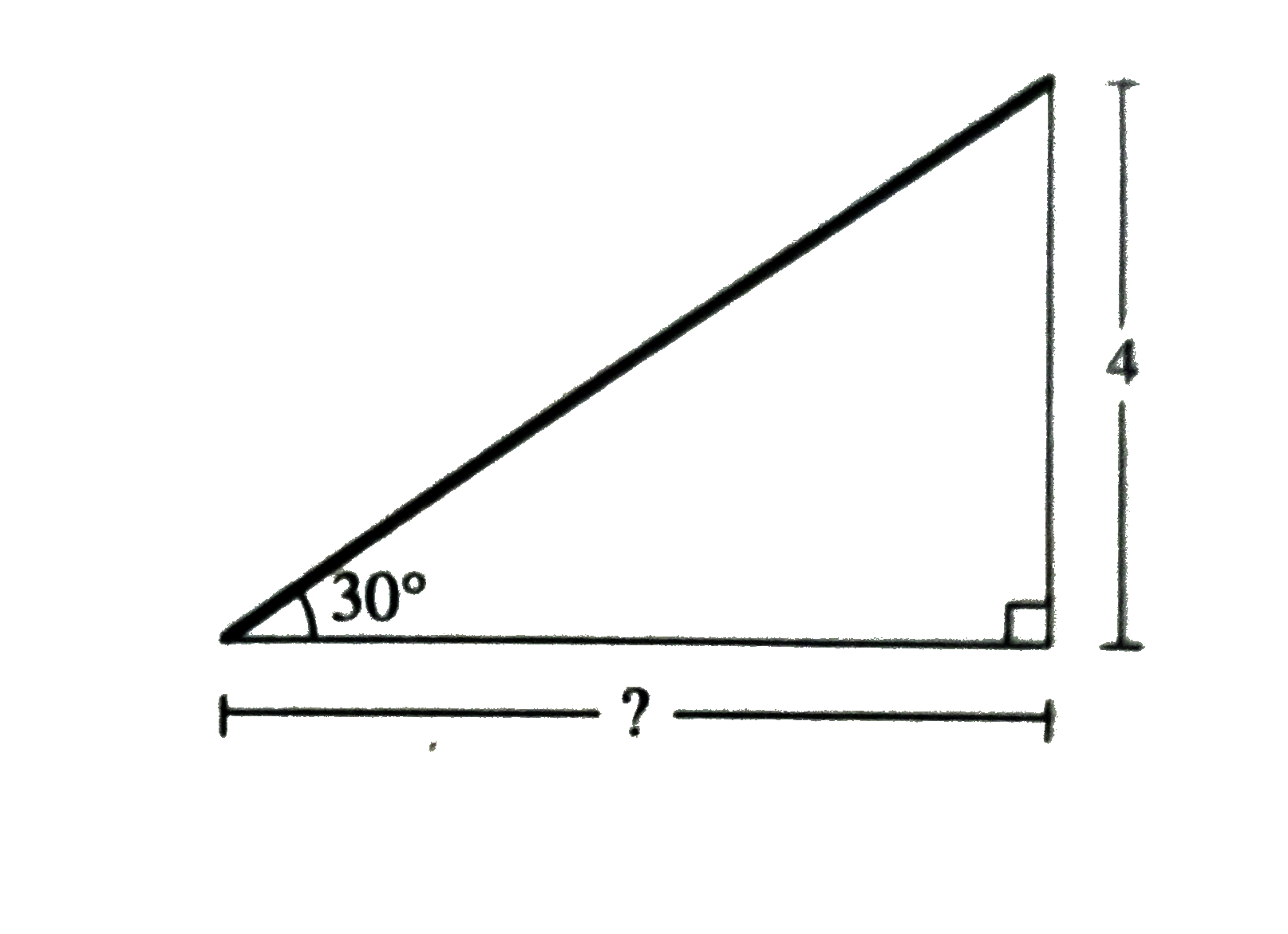
View SolutionA uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ=30.0∘ .
(a) The ball descends a vertical height h = 1.20 m to reach the bottom of the ramp. What is its speed at the bottom?
View SolutionA uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle theta = 12^(@) with the horizontal. The objects roll smoothly down the ramp. (a) Which object wins the race to the bottom of the ramp?
View Solution
