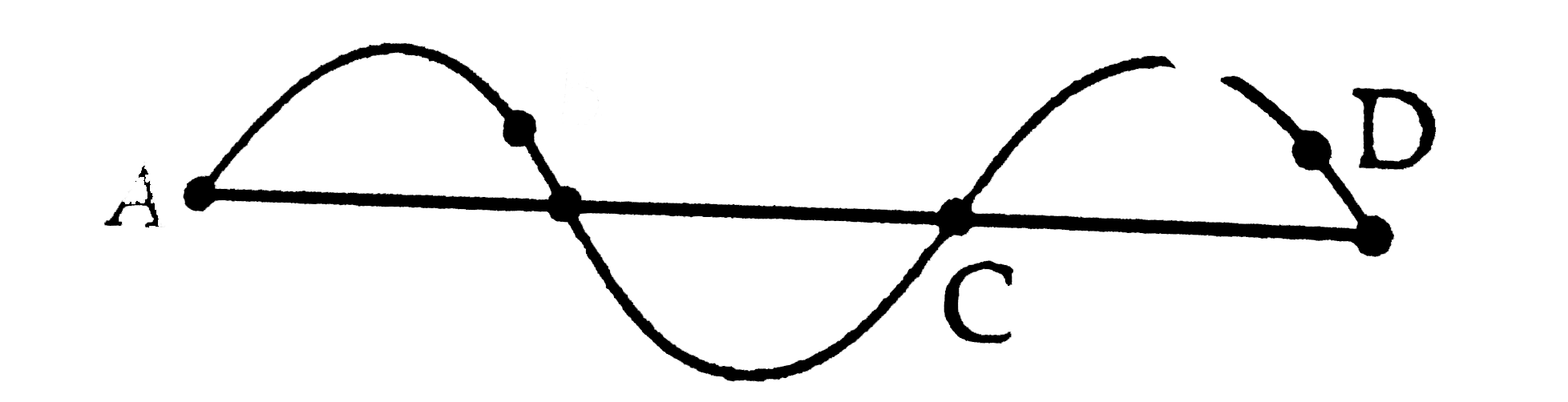
In case of reflection of a wavefront from a reflecting surface,

I. points A and E are in same phase.
II. Points A and C are in same phase.
III points A and B are in same phase.
IV. Points C and E are in same phase.
Which of the following is correct?
A
I and II
B
II and III
C
III and IV
D
I and IV
Text Solution
The correct Answer is:C
Figure shows AB as incident wavefront, so A and B are in same phase.

By the time B reaches C, secondary wavelet from A reaches E.
So, points C and E are same time intervals apart as they are in same phase.
|
Topper's Solved these Questions
- WAVE THEORY OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE THEORY OF LIGHT EXERCISE - EXERCISE 2 (Miscellaneous Problems)
18 Videos
- WAVE THEORY OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE THEORY OF LIGHT EXERCISE - MHT CET CORNER
4 Videos
- WAVE THEORY OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE THEORY OF LIGHT EXERCISE - MHT CET CORNER
4 Videos
- WAVE MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER
23 Videos
Similar Questions
Knowledge Check
The minimum distance between the two points having the same phase is
Awavelength of the waveBamplitude of the waveCwave numberDfrequency of the waveThe diagram below shows the propagation of a wave. Which points are in same phase?
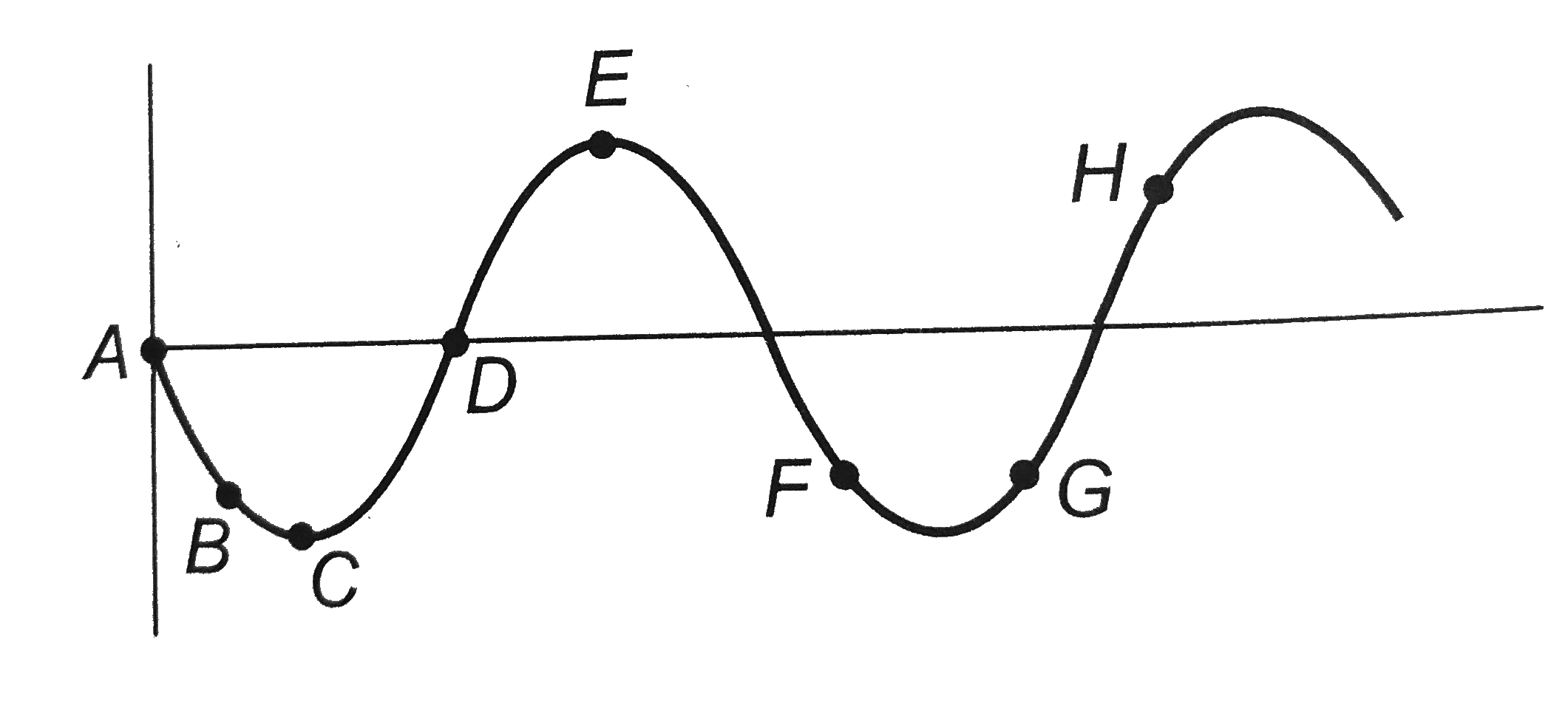 .AF and GBC and FCB and GDB and F
.AF and GBC and FCB and GDB and FConsider a reaction A+B→C , in which boht reactants are in the same phase, may be
Aunimolecular elementary reactionBExothermicCHeterogeneousDPhotochemical
Two waves of amplitudes 3mmand2mm reach a point in the same phase. What is the resultant amplitude ?
View SolutionThe distance between two consecutive points in the same phase is called
View SolutionPhase difference between any two points of a wavefront is
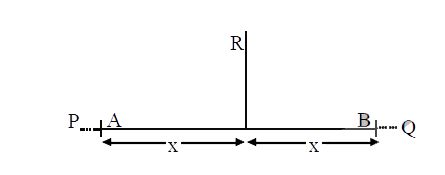
View SolutionThe frequencies of sources A and B as shown in figure are same. The nature of interference at points P, Q and R will be if AB=λ2 and the two sources are in same phase.
View SolutionThe locus of all points of the medium having the same phase for particles of light is called
View Solution