In Fig. coil 1 and coil 2 are wound on a long cylindrical insulator. The ends A' and B are joined together and current I is passed. Self-inductance of the two coils are L1 and L2, and their mutual inductance is M.
a. Show that this combination can be replaced by a single coil of equivalent inductange given by
Leq=L1+L2+2M.
b. How could the coils be reconnected by yieldings an equivalent inductance of Leq=L1+L2−2M.

When the termial A' and B are connected, the sence of current in both the coil is same. Let the current be changing at the rate of dI/dt. The magnetic fields of both coil 1 and coil 2 point toward left. When the current increases, both fields increases and both the changes in flux contribute emfs in the same direction. Thus, the induced emf in coil 1 is
E1=−(L1+M)dIdt (i)
Similarly, the magnetic field in coil 2 due to it and field due to coil 1 point toward left. The two induced emfs are again in the same direction.
E2=−(L2+M)dIdt (ii)
Hence, the total emf across both the coils is
E=E1+E2=−(L1+L2+2M)dIdt (iii)
If these coils were replaced by a single coil, then we have
E=−LeqdIdt (iv)
On comparing Eqs (iii) and (iv), we have
Leq=L1+L2+2M
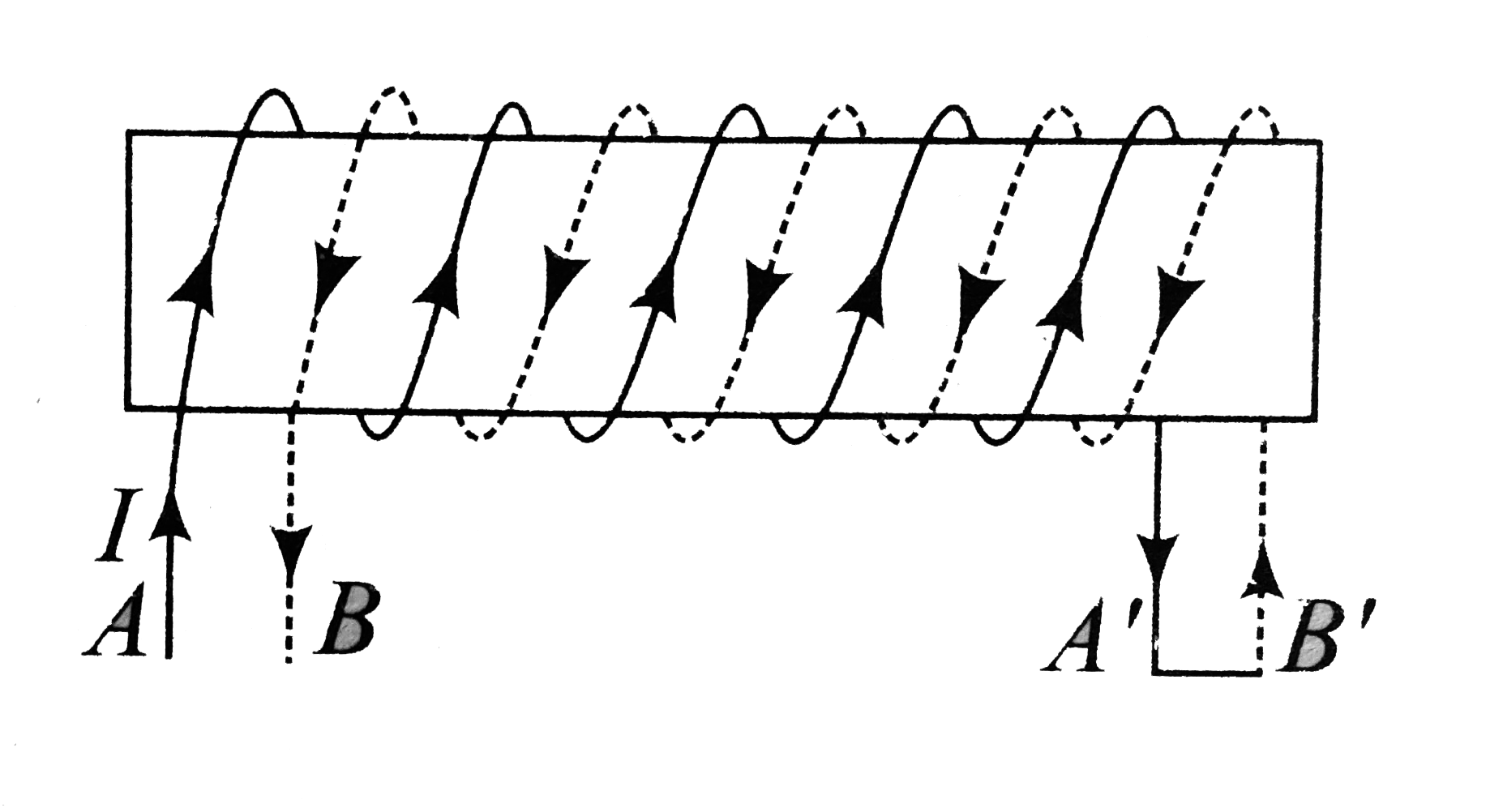
b.When terminals A' and B are connected, the sense of the flow of current in coil 1 is opposite to that in coil 2. Then at the site of coil 1 the field produced by coil 2is opposite to the field produced by coil 1 itself. An increasing current in coil 1 tends to increase the flux in that coil but an increasing current on coil 2 tends to decrease it. The emf across coil 1 is
E1=−(L1−M)dIdt
Similarly, emf across coil 2 is E2=−(L2−M)dIdt.
The total emf E=E1+E2=−(L1+L2−2M)dIdt
Thus, Leq=(L1+L2−2M)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.124videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit28videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
Similar Questions
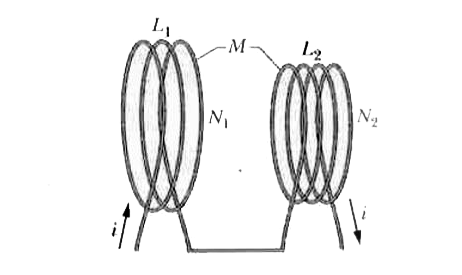
Two coils connected as shown in Fig. 30-48 separately have inductances L1 and L2. Their mutual inductance is M. (a) Show that this combination can be replaced by a single coil of equivalent inductance given by
Leq=L1+L2+2M
(b) How could the coils in Fig. 30-48 be reconnected to yield an equivalent inductance of
Leq=L1+L2−2M?
 View Solution
View SolutionEnergy needed to establish an alternating current I in a coil of self inductance L is
View Solution
Knowledge Check
- Question 1 - Select One
Mutual inductance of two coils depends on their self inductance L1 and L2 as :
AM12=L1/L2BM12=L2/L1CM12=√L1L2DM12=√L1/L2 - Question 2 - Select One
The self-inductances of two identical coils are 0.1H. They are wound over each other. Mutual inductance will be-
A0.1HB0.2HC0.01HD0.05H - Question 3 - Select One or More
The mutual inductance M12 of coil 1 with respect to coil 2
Aincreases when they are brought nearerBdepends on the current passing through the coilsCincreases when one of them is rotated about an axisDis the same as M21 coil 2 with respect to coil 1
Derive an expression for the total magnetic energy stored in two coils with inductances L1 and L2 and mutual inductance M, when the currents in the coils are I1 and I2, respectively.
View SolutionWhen a current I is established in a coil of self-inductance L, energy stored in the inductor is ______.
View SolutionThe inductors of self inductance L1 and L2 are put in series .
View SolutionEnergy required to establish a current of 4 A in a coil of self-inductance L=200 mH is
View SolutionIf the rate of change of current is 1A per second in one coil induces an emf of 2 V in the neighbouring coil, the mutual inductance of two coils is
View Solution

