In Fig. Find the magnetic field at common centre.

Consider Fig.
→BP=(→B1)P+(→B2)P+(→B3)P+(→B4)P+(→B5)P
where (→B1)P=μ0i4π(3a2)(−ˆj) (semi-infinite wire)
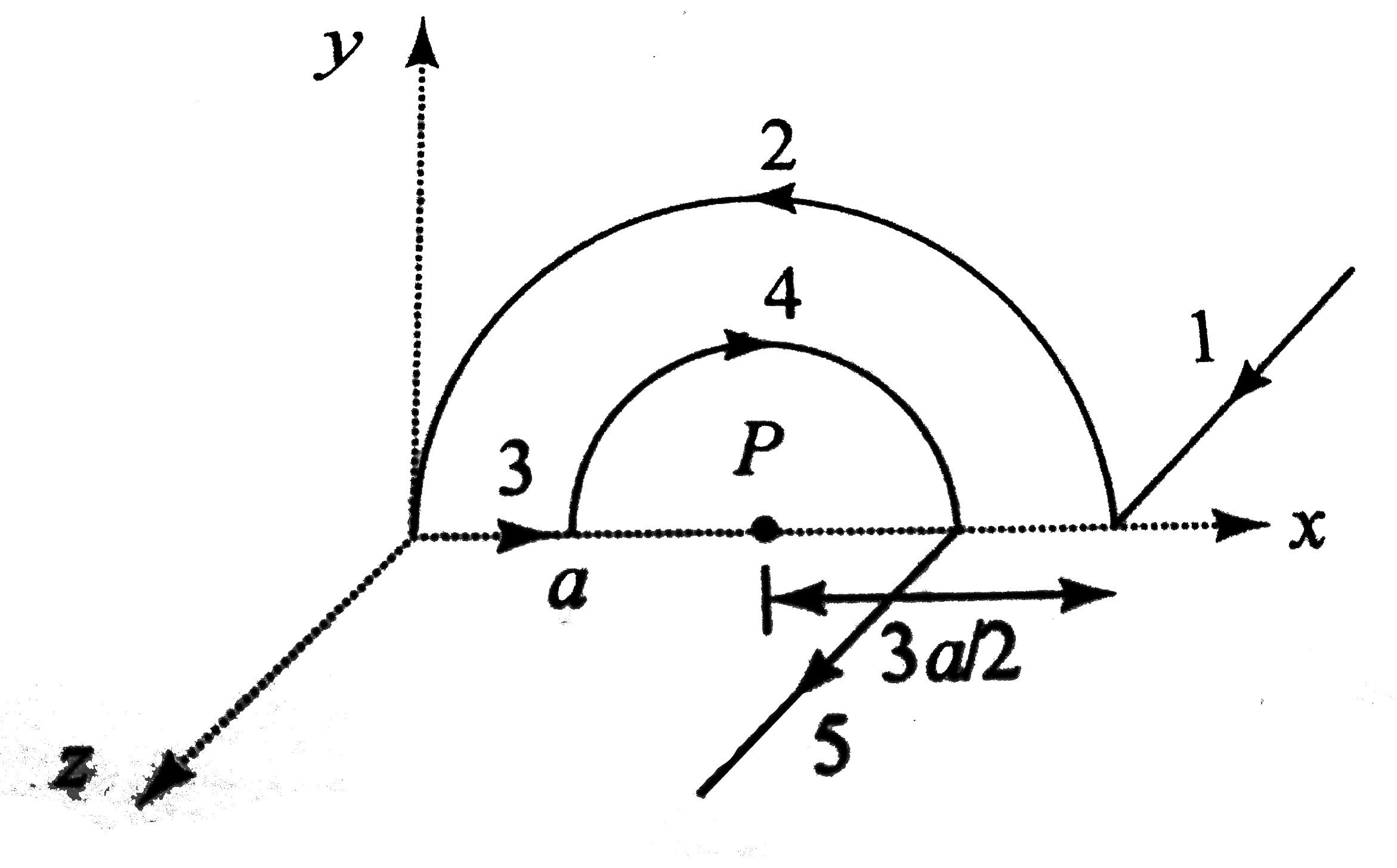
(→B2)P=μ0i4π(3a2)(−ˆk)
(→B3)P=0
(→B4)P=μ0i4(a2)(−ˆk)⇒(→B5)P=μ0i4π(a2)(−ˆj)
(→B)P=μ0i2a[−(13π+1π)ˆj−(1−13)ˆk]
→BP=μ0i3a[2πˆj−ˆk]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
In Fig, find the magnetic field at point P.
 View Solution
View SolutionFind magnetic field at O.
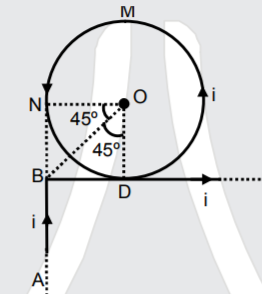 View Solution
View SolutionAn otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
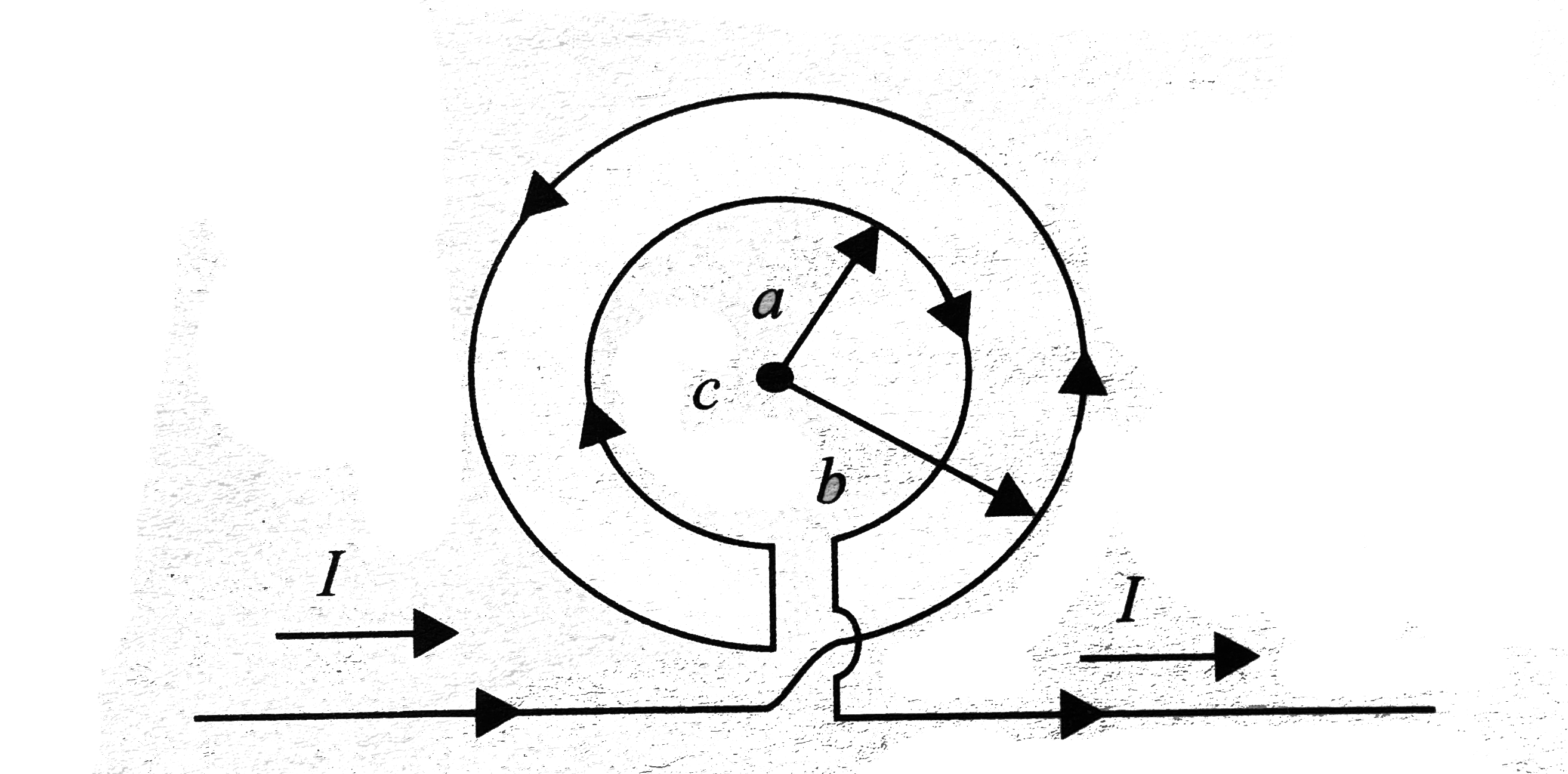 View Solution
View SolutionThe wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.
 View Solution
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.
 View Solution
View SolutionFor the arrangement shown in Fig. determine the magnetic field at centre O.
 View Solution
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
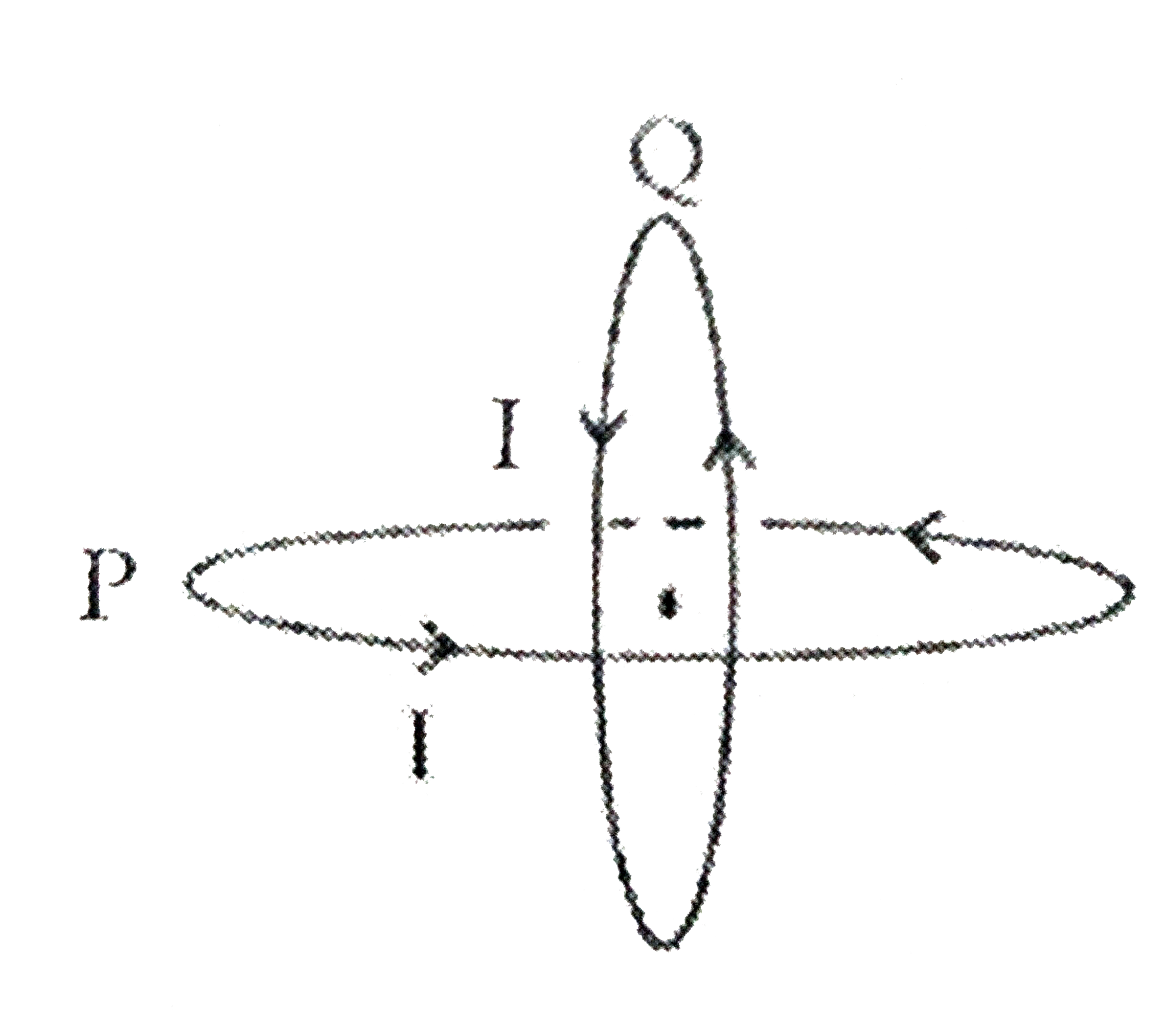 View Solution
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View SolutionA regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
View Solution

