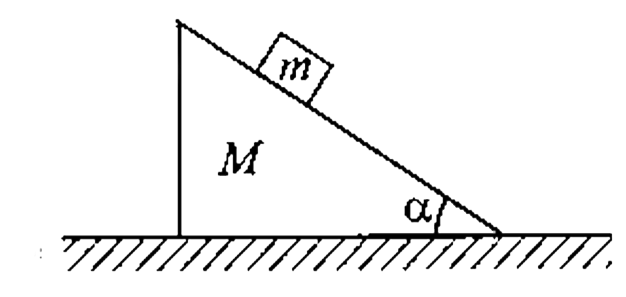
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
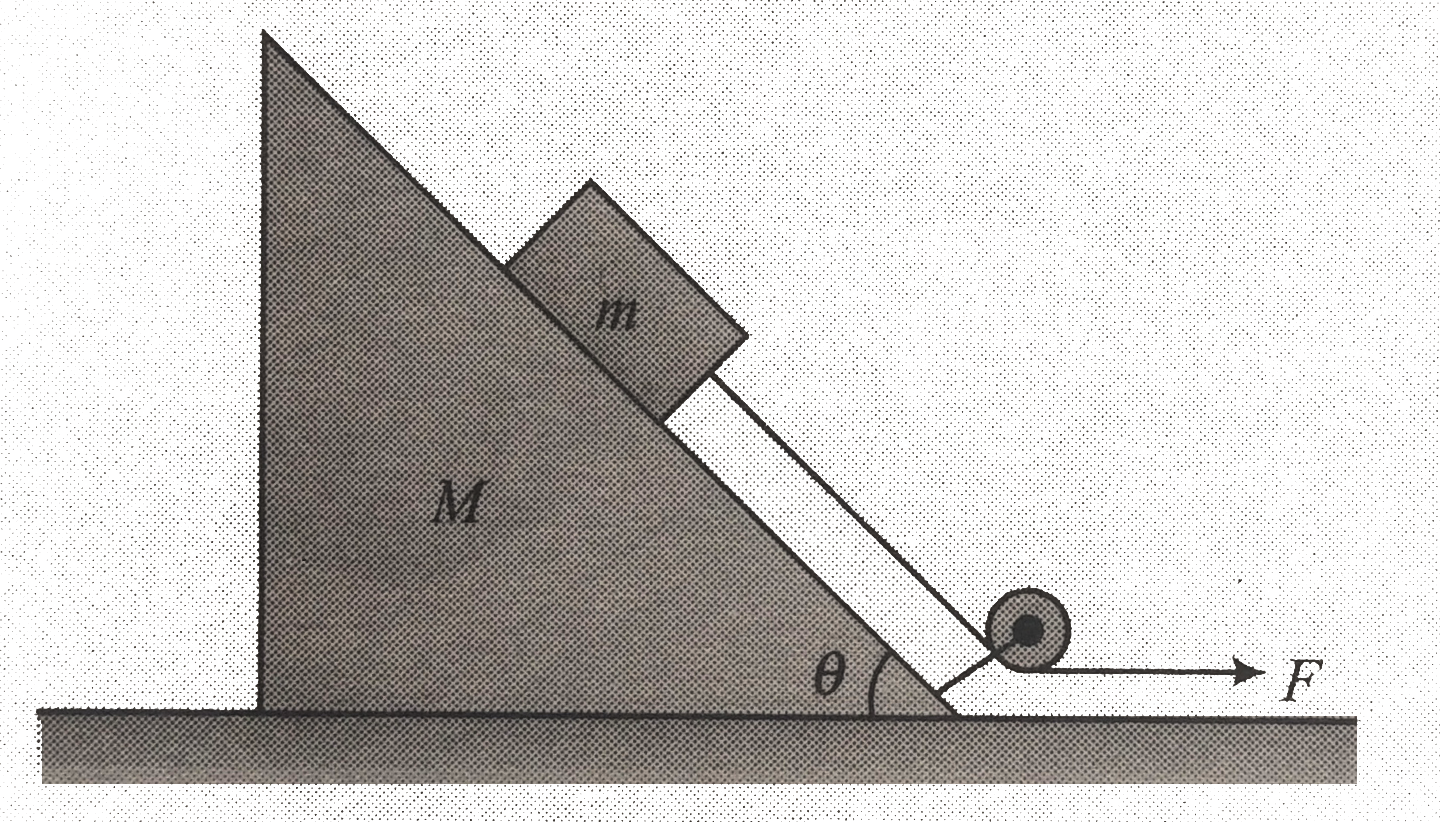
Constraint relation
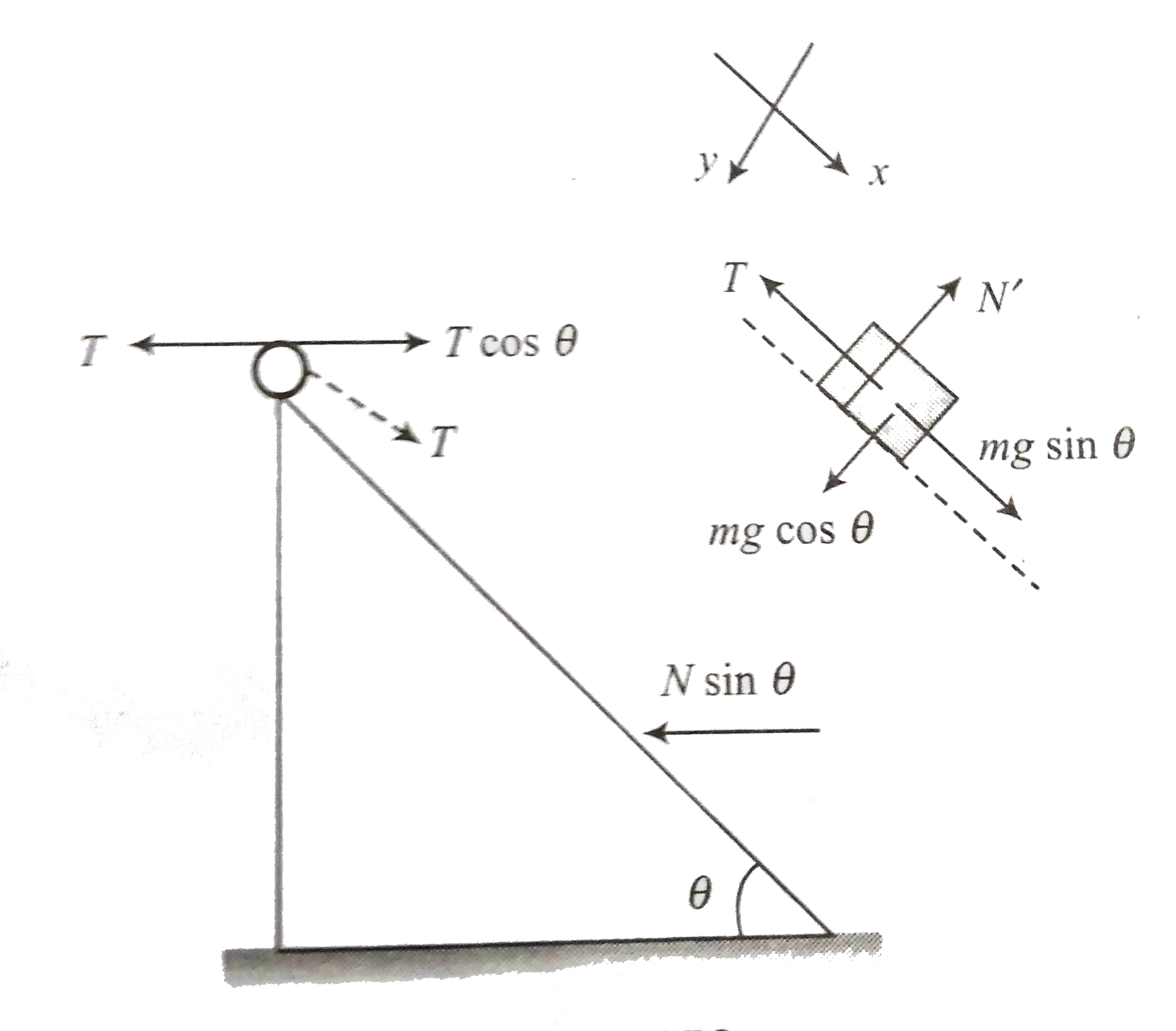
It is clear from above discussion
ax=A(1−cosθ)
and ay=Asinθ
Equations of motion
Considering the motion of wedge in horizontal direction
For wedge
T=Tcosθ+Nsinθ=MA
Considering the motion of block parallel and perpendicular to the sloping side in horizontal direction
For block: In the direction parallel to inclined surface,
mgsinθ−T=max=MA(1−cosθ)
or T=mgsinθ=MA(1−cosθ) ...(ii) In the direction perpendicular to inclined plane,
mgcosθ−N=may=mAsinθ
N=mgcosθ=mAsinθ ...(iii)
Substituting the value of N from (ii) and (iii) in (i) we get,
A=mgsinθM+2m(1−cosθ).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
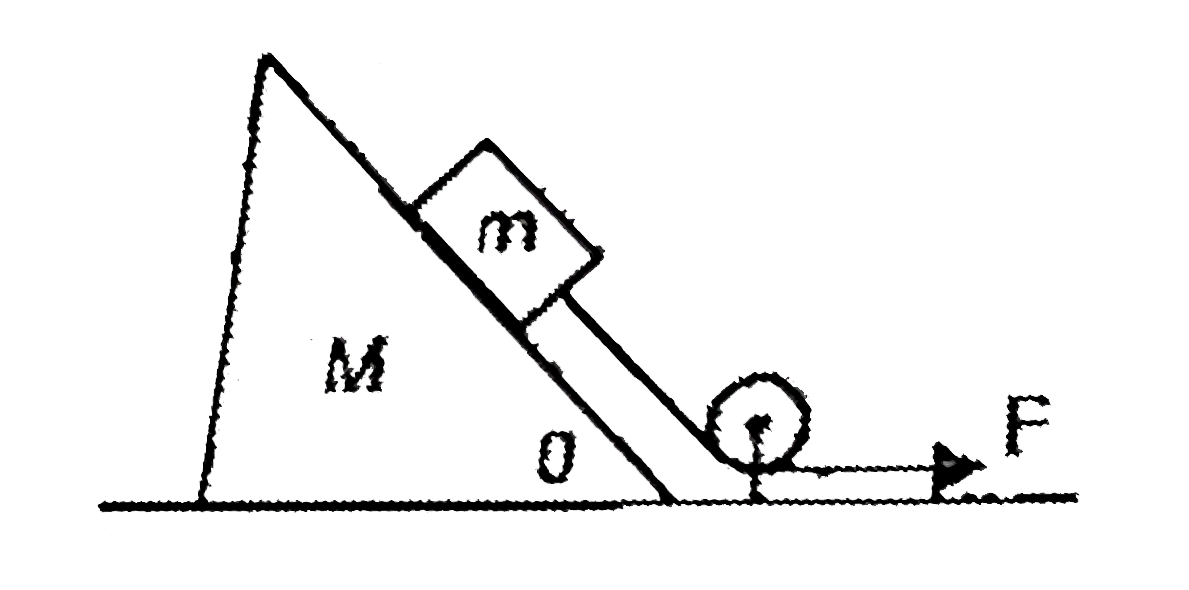 View Solution
View SolutionIn the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
All surfaces are smooth. The acceleration of mass m relative to the wedge is
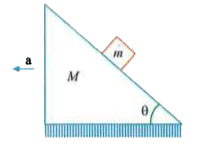 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 2 - Select One
All surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 3 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
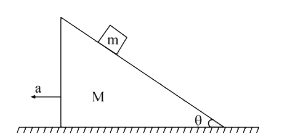 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
 View Solution
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.
 View Solution
View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.
 View Solution
View SolutionIn the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View SolutionIn the arrangement shown in figure wedge of mass M moves towards left with an acceleration a. All surfaces are smooth. The acceleration of mass m relative to wedge is
 View Solution
View Solution

