In Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

The velocity of the rod as function of time is
(a) EBl(1−e−t/τ)
(b) EBl(1+e−t/τ)
( c) 32EBl(1−e−t/τ)
(d) E2Bl(1−e−t/τ)
The correct Answer is:A
(a)Due to applied emf, current will flow as shown. Due to this current and magnetic field B, force on the wire will act towards right and rod will start moving towards right. Let at any instant, its velocity, emf e=Blv will be induced as shown.

Net emf: E−Blv,I=E−BlvR ....(i)
F=IBl=(E−BlvR)Bl ...(ii)
→ mdvdt=(E−Blv)BlR
mRBldvdt=E−Blvrarr∫v0dvE−Blv=∫t0BlmRdt
→ [1n(E−Blv)−Bl]v0=BlmRt → 1n(E−BlvE)=−B2l2mRt
→ E−BlvE=et/τ → v=EBl[1−et/τ]
Velocity will increase upto t∞, and t=∞, velocity will be maximum and constant.
Also, when the velocity is constant, net force on the rod will become zero, so putting F=0 in equation (ii), we get
vterminal=EBl
hen the rod attains terminal velocity, then from equation (i), I=0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
In Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

The current when the rod attains its terminal speed is
View SolutionIn Fig. shown, the rod has a resistance R, the horizontal rails have negligible friction. A battery of emf E and negligible internal resistance is connected between points aandb. The rod is released from rest.

after some time, the rod will approach a terminal speed . Find an expression for it.
View SolutionA series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depends upon
View SolutionA 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be

View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
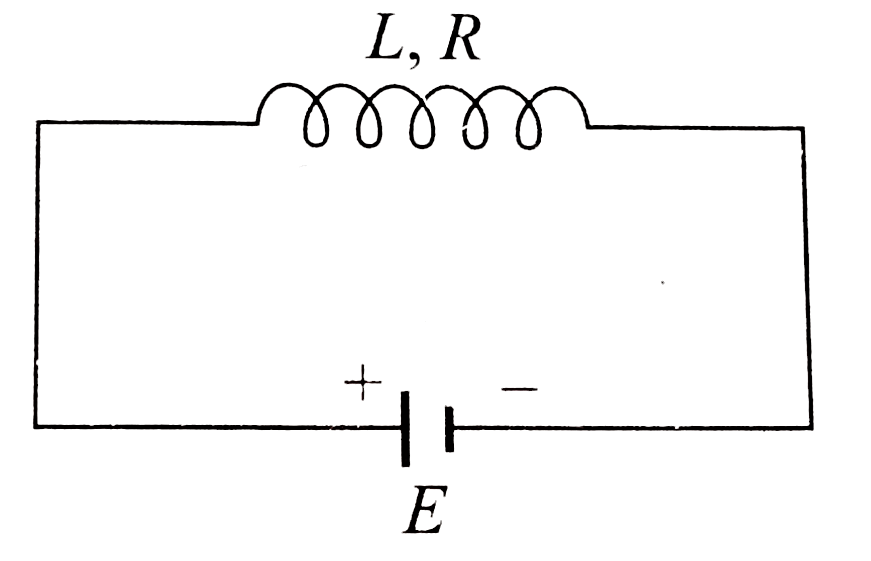
Power supplied by the battery as a function of time
View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
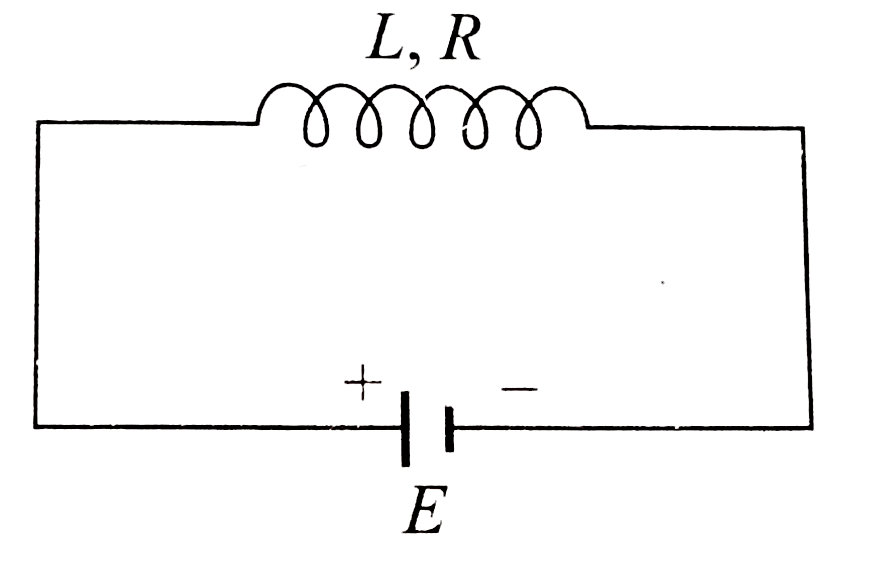
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this is
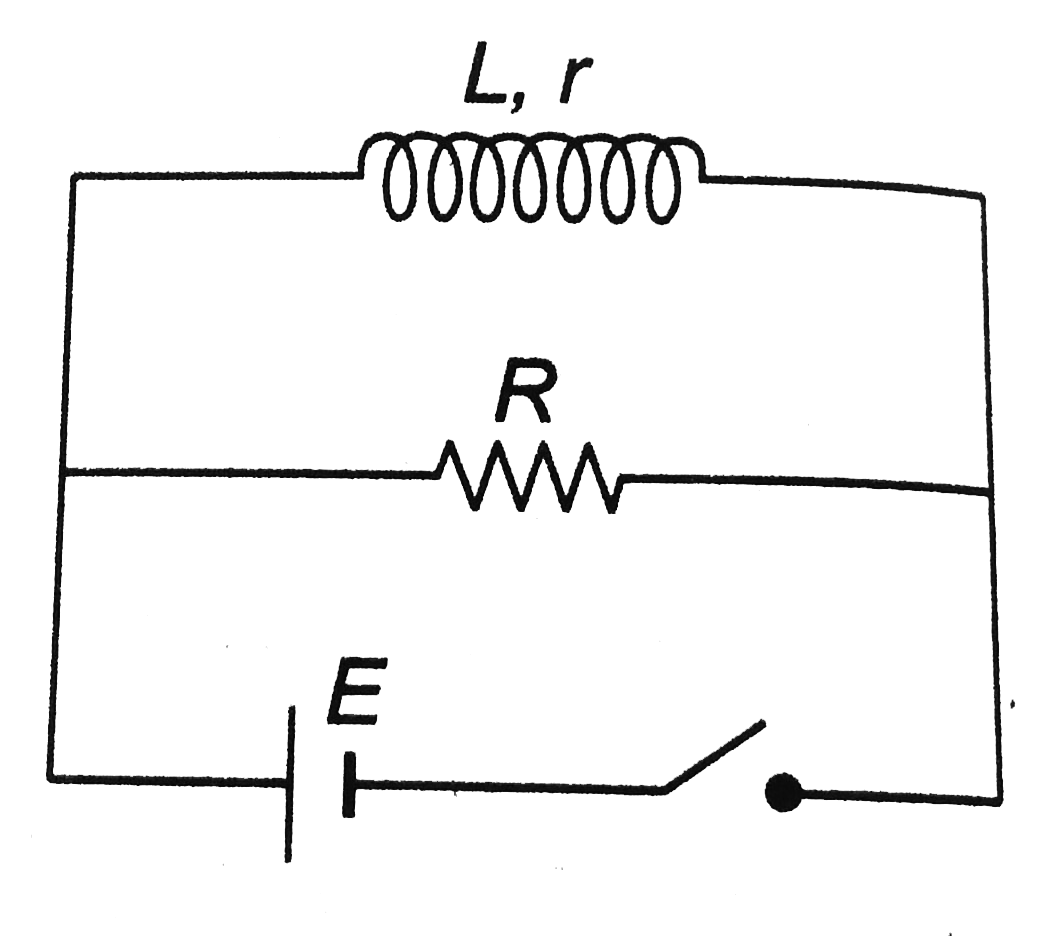
View SolutionA solenoid of inductance L with resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time t=0, switch S is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
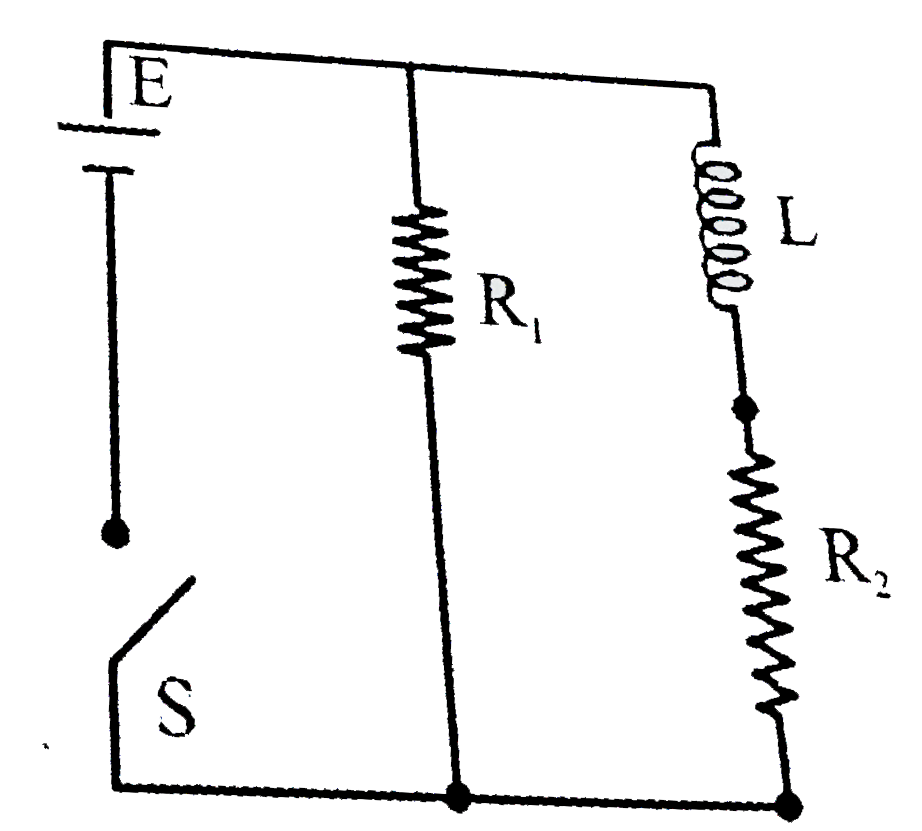
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is

View Solution
