In Fig. the circular and the straight parts of the wire are made of same material but have different diameters. The magnetic field at the centre is zero.

Ratio of the currents I1andI2 flowing through the circular and straight parts is
√32π
2√2π
3√32π
3√32√2π
The correct Answer is:C
(c) If I1andI2 be the currents in circular and straight parts,
respectively, and B1,B2 the magnetic field due to them, then
→B1=μ0I12R×23=μ0I13R
B2=μ0I24π[Rcos60∘][2sin60∘]=√3μ0I22πR
For the total field at 'O' to be zero,
μ0I13R=√3μ0I22πR⇒I1I2=3√32π
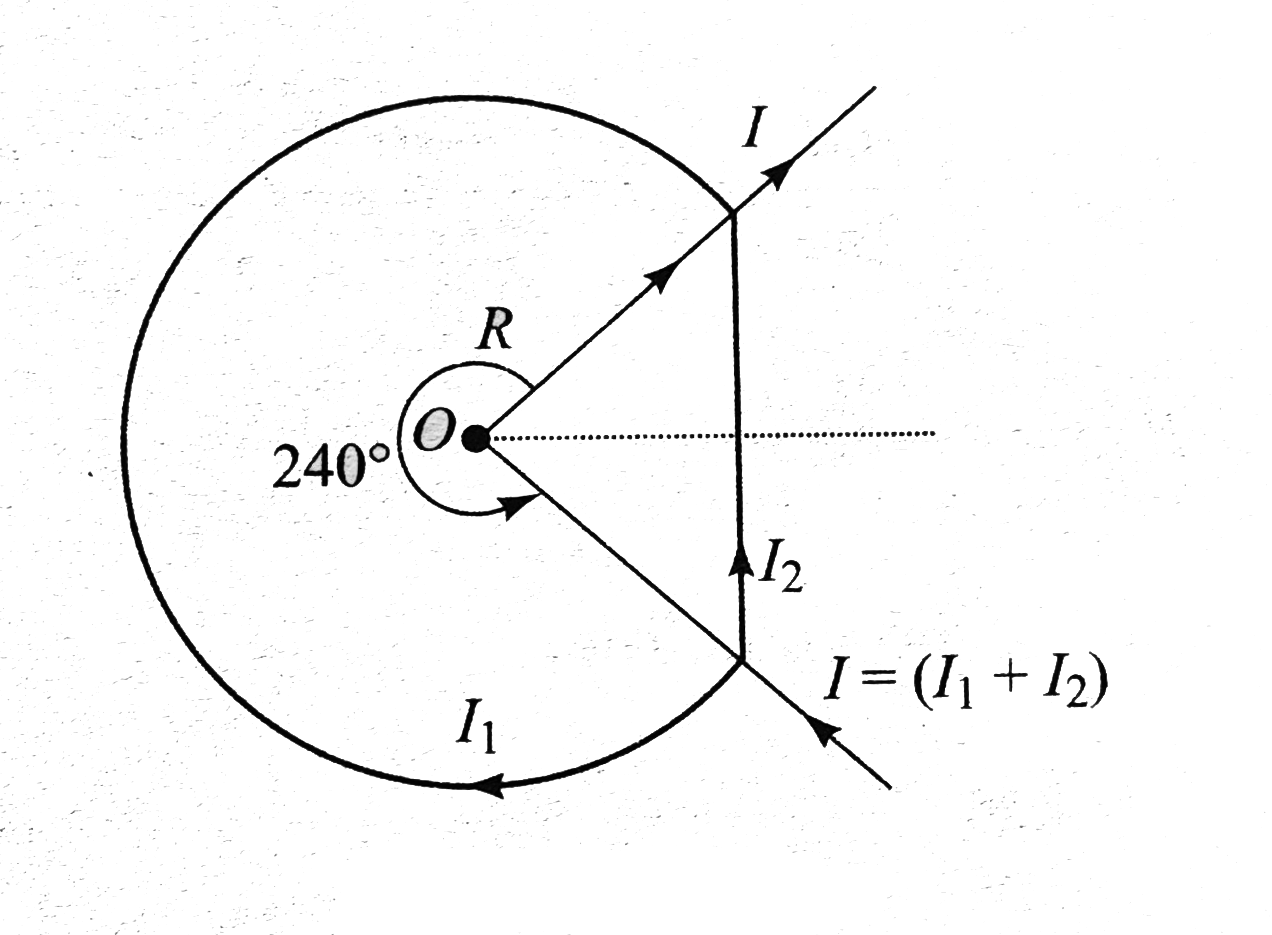
From R=ρlA
R1R2=l1l2A2A1⇒V/I1V/I2=l1l2(π/4)d22(π/4)d21⇒d1d2=√l1I1l2I2
where l1=2πR(23)=43πRandl2=2Rsin60∘=√3R
⇒d1d2=√4πR3√3R3√32π=√2
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)
7 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
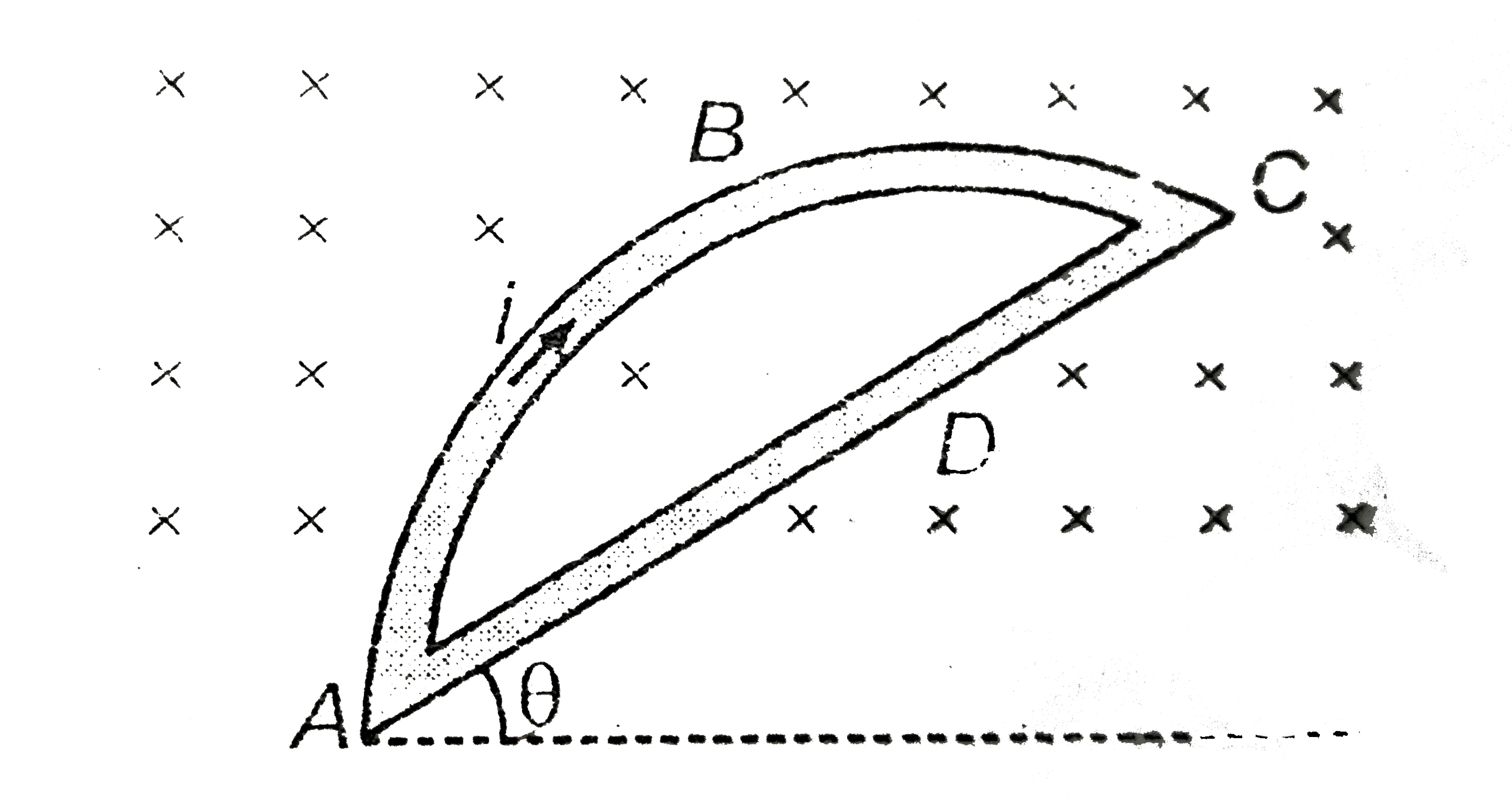
A circular wire ABC and a straight conductor ADC are carrying current i and are kept in the magnetic field B then considering points A and C
View SolutionTwo wires of the same material but of different diameters carry the same current i. If the ratio of their diameters is 2:1 , then the corresponding ratio of their mean drift velocities will be
View Solution
Knowledge Check
In Fig. the circular and the straight parts of the wire are made of same material but have different diameters. The magnetic field at the centre is zero.

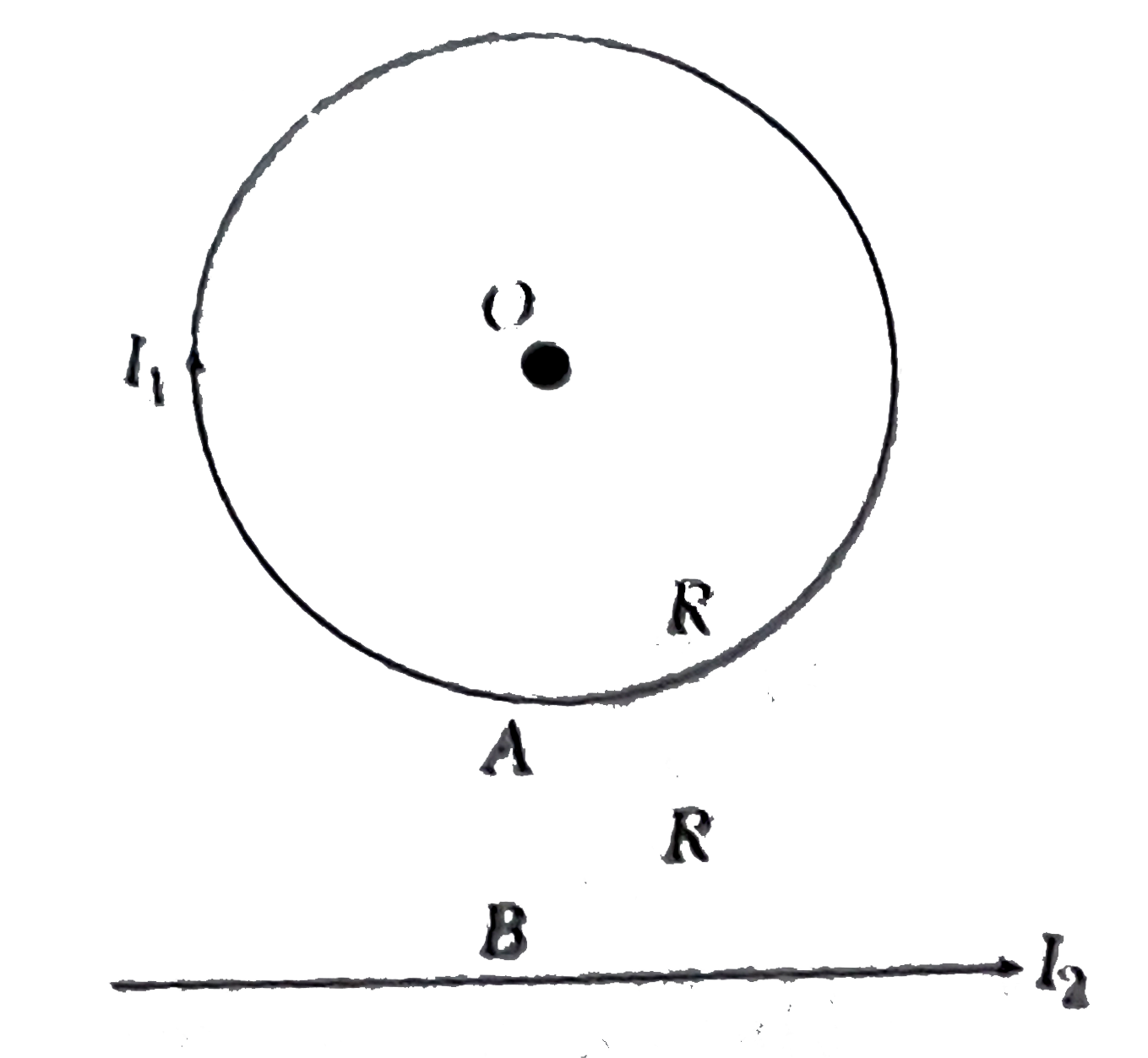
The ratio of the diameters of wires of circular and straight parts isA1√2B2√3πC3√32πD√2In the diagram I1,I2 are the strength of the currents in the loop and straight conductors respectively OA=AB=R. the net magnetic field at the centre O is zero . Then the ratio of the currents in the loop and the straight conductor is
 AπB2πC1πD12π
AπB2πC1πD12πTo produce a magnetic field of π tesla at the centre of circular loop of diameter 1 m, the current flowing through loop is :
A5×106AB107AC2.5×106AD2×106A
The figure shows a current- carrying loop, some part of which is circular and some part is a line segement. The magnetic induction at the centre is

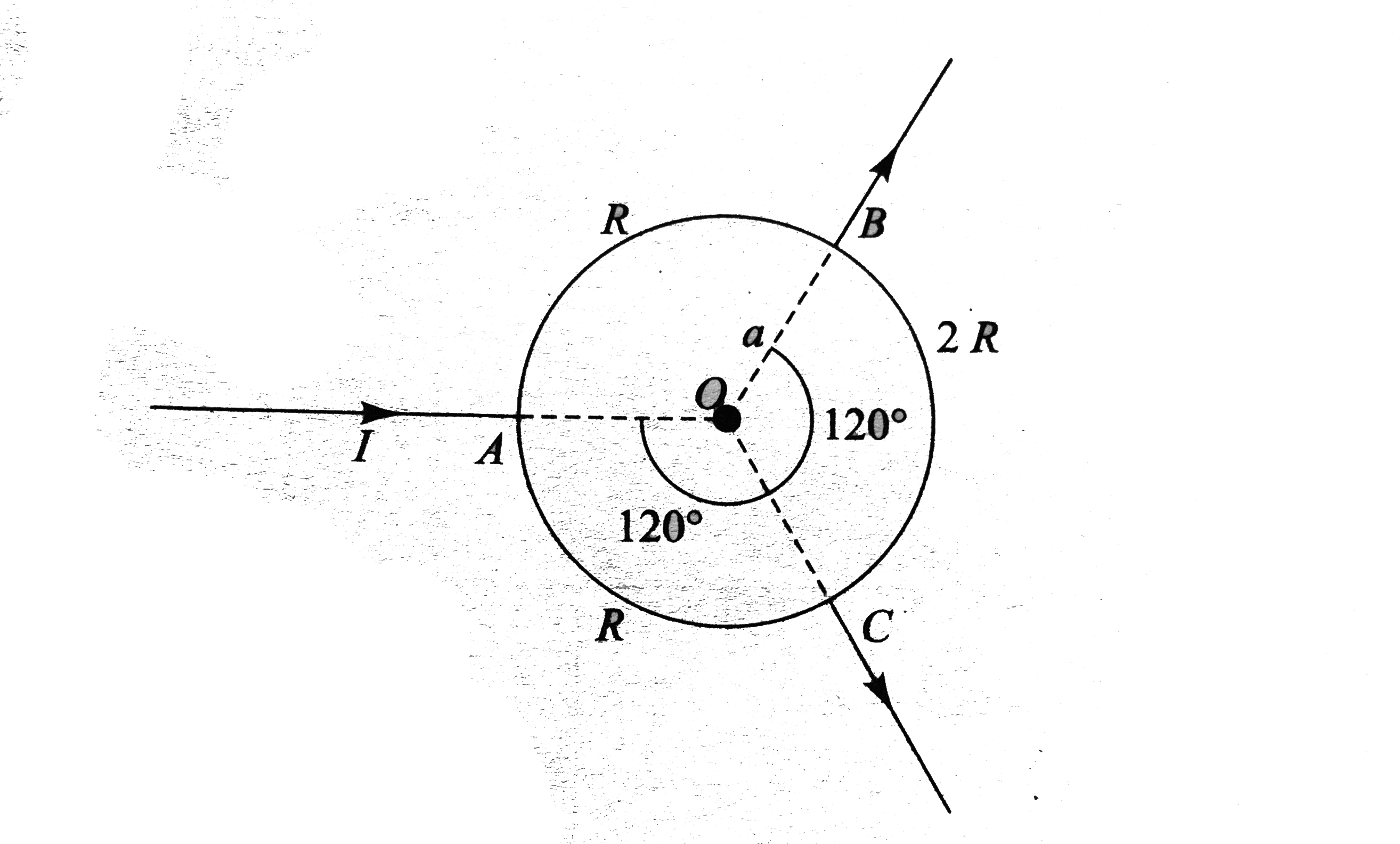
View SolutionThe resistances of three parts of a circular loop are as shown in Fig. The magnetic field at the centre O is (current enters at A and leaves at B and C as shown)
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop

View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a square coil made from the same length of wire will be
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View Solution
