According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
B=μ0I4πr(sinϕ1+sinϕ2)
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

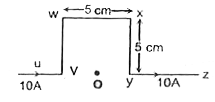
Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given OA=OB=OC=a. Find the magnetic field at point B due to this loop.

A
−μ0I4π(√2a)(ˆi+ˆj)
B
−μ0I4π(√2a)(ˆj+ˆi)
C
−μ0I2(√2π)(ˆj+ˆi)
D
none of these
Video Solution
Text Solution
The correct Answer is:B
(b)
At B, magnetic field will be zero due to CB and AB parts.
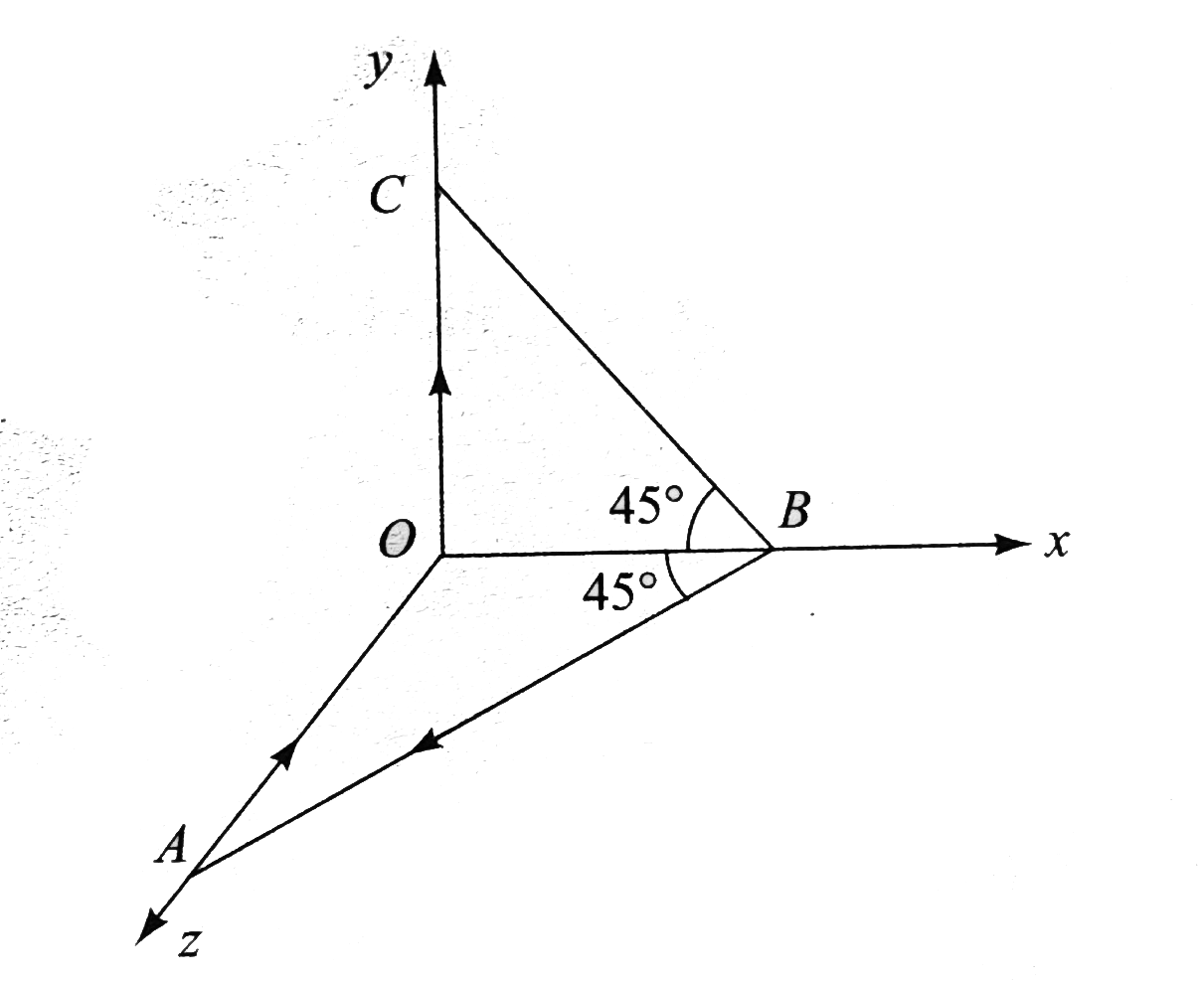
→BAO=μ04πIa[sin0∘+sin45∘](−ˆj)=−μ0I4π√2aˆj
→BOC=μ04πIa[sin0∘+sin45∘](−ˆk)=−μ0I4π√2aˆk
Net magnetic field at B
=→BAO+→BOC=−μ0I4π√2a(ˆj+ˆk)
At O, magnetic field due to AO and OC will be zero.
Due. to BC: r=acos45∘=a√2
→BCB=μ04πIr[sin45∘+sin45∘](−ˆk)=−μ0I2πaˆk
Similarly, due to BA: →BBA=−μ0I2πaˆj
Net magnetic field =→BCA+→BBA=−μ0I2πa(ˆj+ˆk)
|
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)
7 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
B=μ0I4πr(sinϕ1+sinϕ2)
The direction of magnetic field being perpendicular to the plane containing the wire and the point.
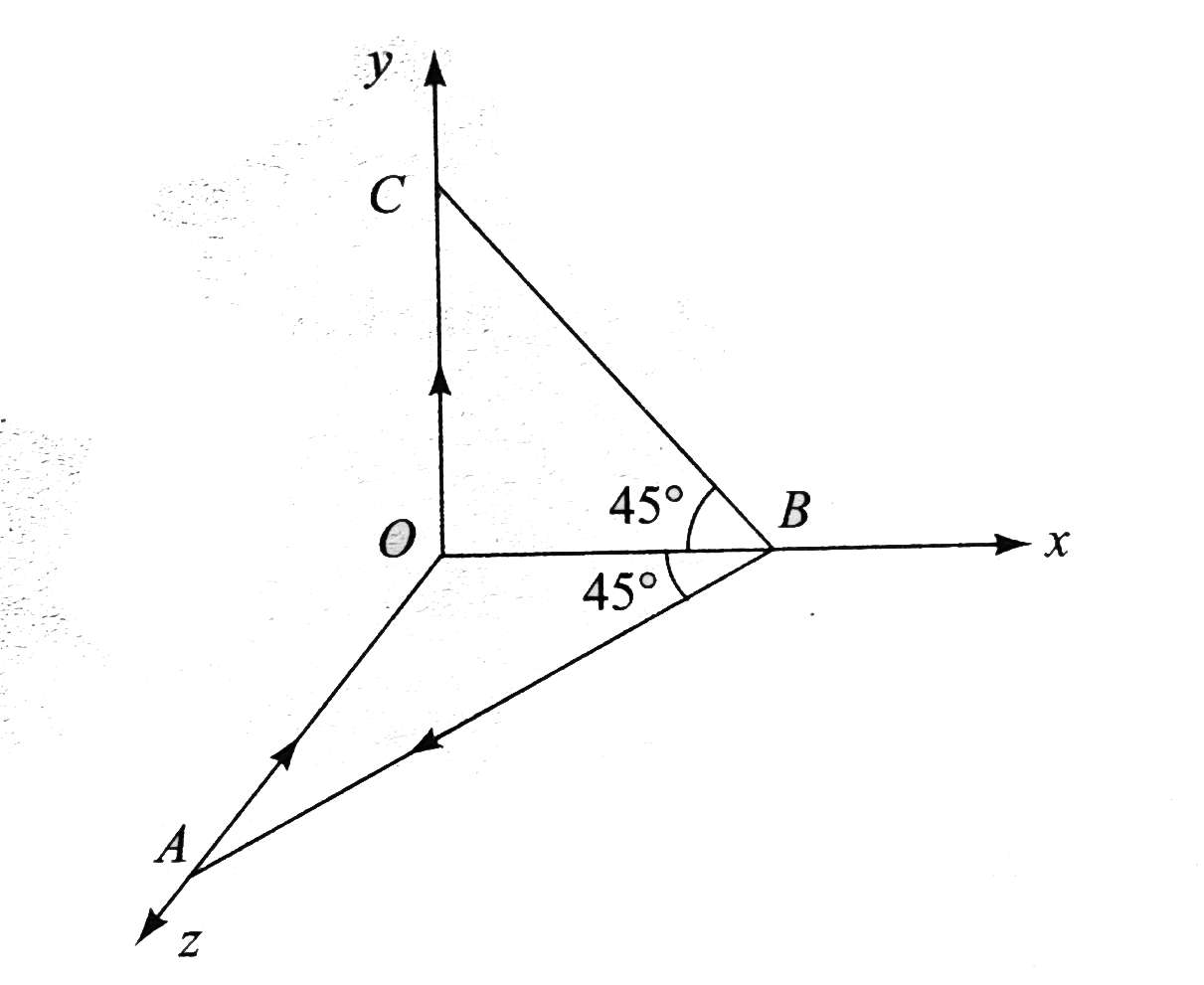
Find magnetic field at point O in Fig.A−μ0I4πa(ˆi+ˆk)B−μ0I4πa(ˆj+ˆk)C−−μ0I2πa(ˆj+ˆk)D−μ0I2√2πa(ˆj+ˆk)The direction of magnetic field at a point due to an infinitely long wire carrying current is
Aparallel to the currentBantiparallel to the currentCalong the perpendicular drawn from a point on the wireDperpendicular to the plane containing the conductor and the pointThe magnetic field at a point P due to a current carrying coil as shown in figure is
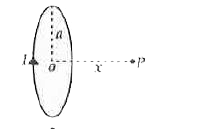 Aμ04π1a2Bμ04πlax(x2−a2)2Cμ04π2πla2x2Dμ04π2πla2(x2+a2)3/2
Aμ04π1a2Bμ04πlax(x2−a2)2Cμ04π2πla2x2Dμ04π2πla2(x2+a2)3/2
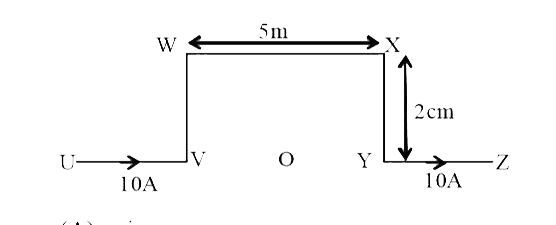
The resulting magnetic field at the point O due to the current carrying wire shown in the figure-
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
View Solution

