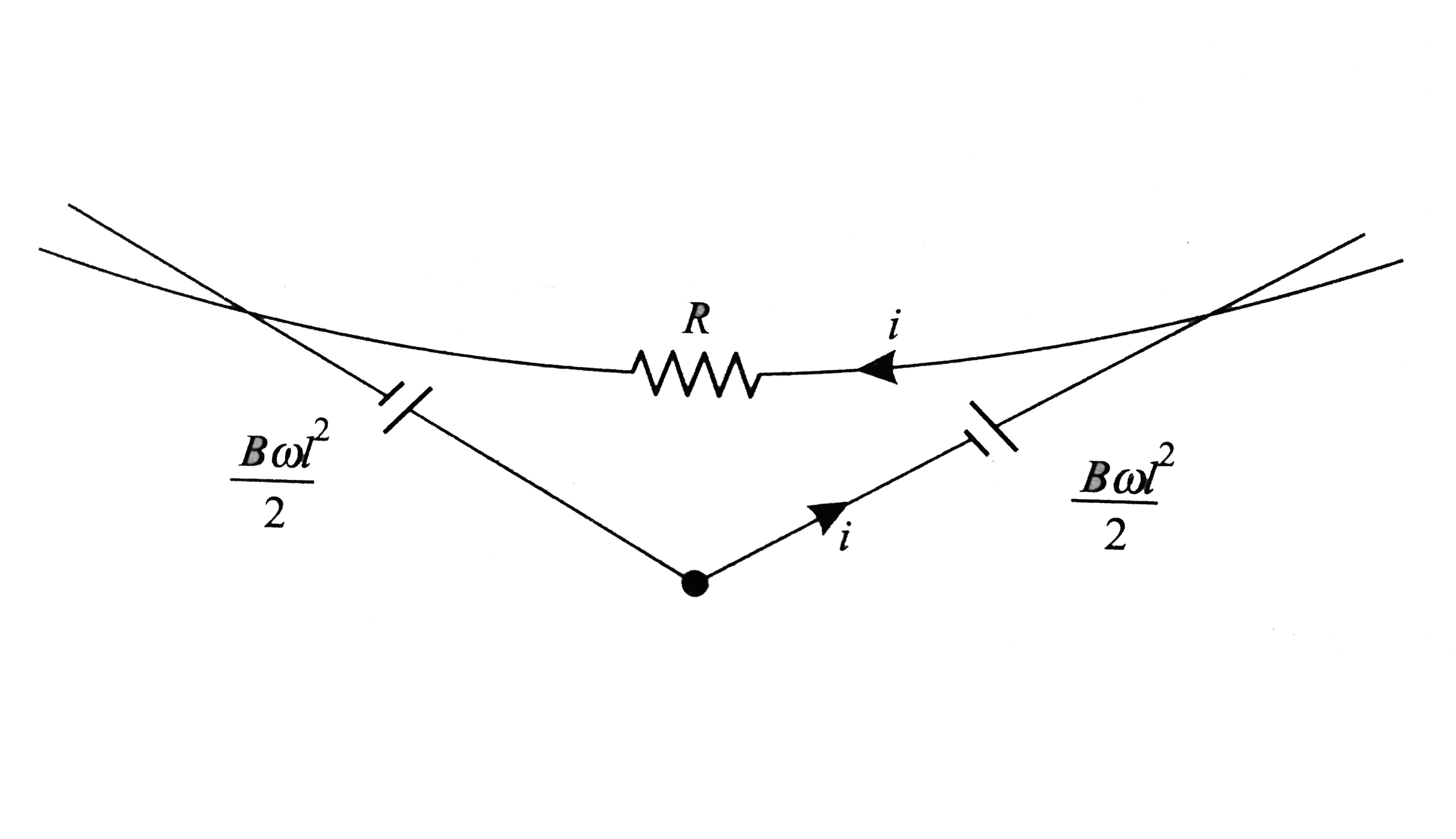
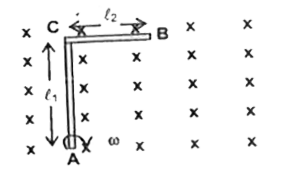
In fig. there exists a uniform magnetic field B into the plane of paper. Wire CD is in the shape of an arc and is fixed. OA and OB are the wires rotating with angular velocity ω as shown in the figure in the same plane as that of the arc about point O. If at some instant, OA=OB=l and each wire makes angle θ=30∘ with y-axis, then teh current through resistance R is (wires OAandOB have no resistance)

(a) 0
(b) Bωl2R
( c) Bωl22R
(d) Bωl24R
The correct Answer is:B
(b) I=Bωl22+Bωl22R=Bωl2R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View Solution
Knowledge Check
For the L shaped conductor in a uniform magnetic field B shown in figure the emf across its ends when it rotates with angular velocity ω about an axis through one its ends O and normal to its plane will be
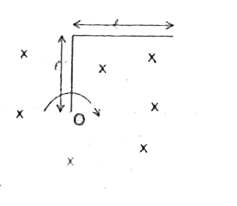 A2Bωl2BBωl2C12Bωl2D4Bωl2
A2Bωl2BBωl2C12Bωl2D4Bωl2A rod OA of length l is rotating (about end O) over a conducting ring in crossed magnetic field B with constant angular velocity ω as shown in figure.
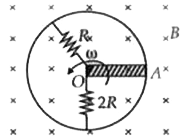 ACurrent flowing through the rod is 3Bωl24RBMagnetic force acting on the rod is 3B2ωl34RCTorque due to magnetic force acting on the rod is 3B2ωl48RDMagnitude of external force that acts perpendicularly at the end of the rod of maintain the constant angular speed is 3B2ωl38R
ACurrent flowing through the rod is 3Bωl24RBMagnetic force acting on the rod is 3B2ωl34RCTorque due to magnetic force acting on the rod is 3B2ωl48RDMagnitude of external force that acts perpendicularly at the end of the rod of maintain the constant angular speed is 3B2ωl38RA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionMagnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
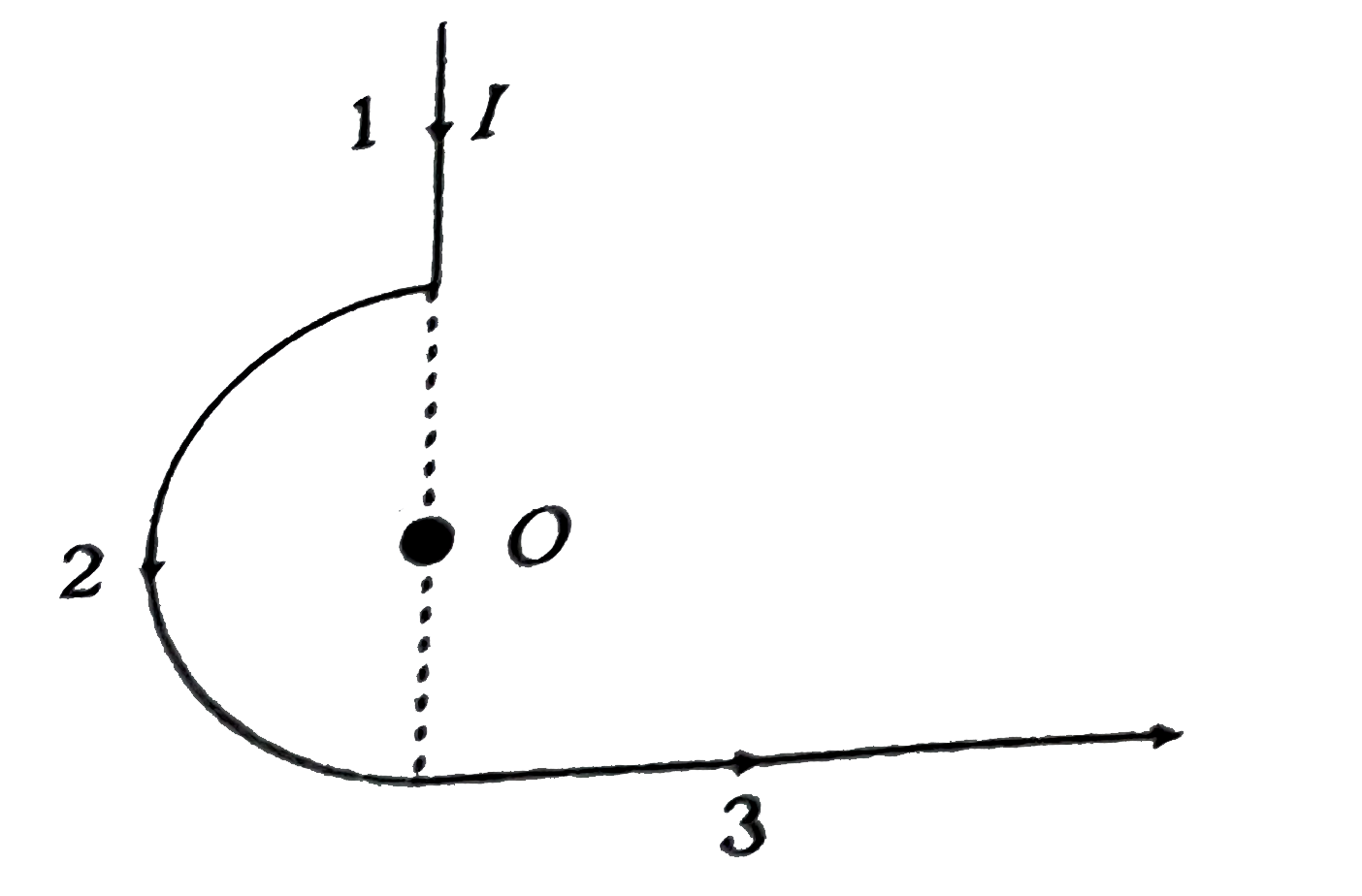
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
View SolutionA circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
View Solution
