the uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
(a) all the points on the ring are at the same potential
(b) the emf induced in the ring is πa2α
( c) electric field intensity E at any point on the ring is zero
(d) E=(aα)/2
The correct Answer is:A, B, D
(a, b, d):
ϕ=πa2B
e=πa2dBdt=πa2α
E2πa=e → E=πa2α2πa=αa2
Let R bethe resistance of the ring. Then current in the ring is I=e/R
Consider a small element dl on the ring,
emf induced in the element, de=(e2πa)dl
resistance of the element, dR=(R2πadl
:. Potentail difference across the element
=de−
=(e2πa)dl−(eR)(R2πa)dl=0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find
a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
View Solution
Knowledge Check
The magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
AThe emf induced in the ring is πr2dBdtBThe emf induced in the rintg is 2πrdBdtCThe potential difference between diametrically opposite points on the ring is half of the induced emf.DAll points on the ring are at the same potential.The magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
Athe emf induced in the ring is πr2dBdtBthe emf induced in the ring is 2πrdBdtCdiametrically opposite points on the ring are at the same potentialDall points on the ring are at the same potentialA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
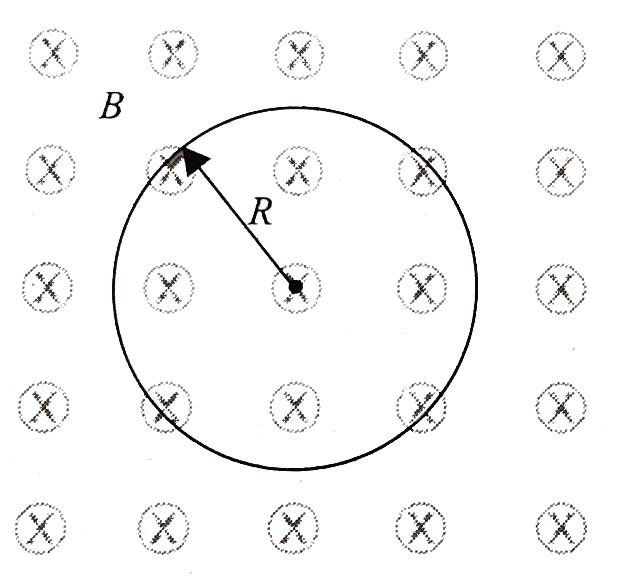A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
The figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
)
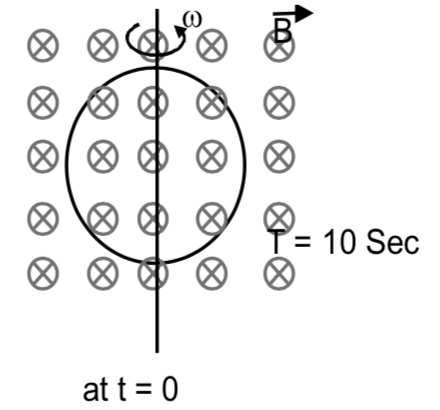View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
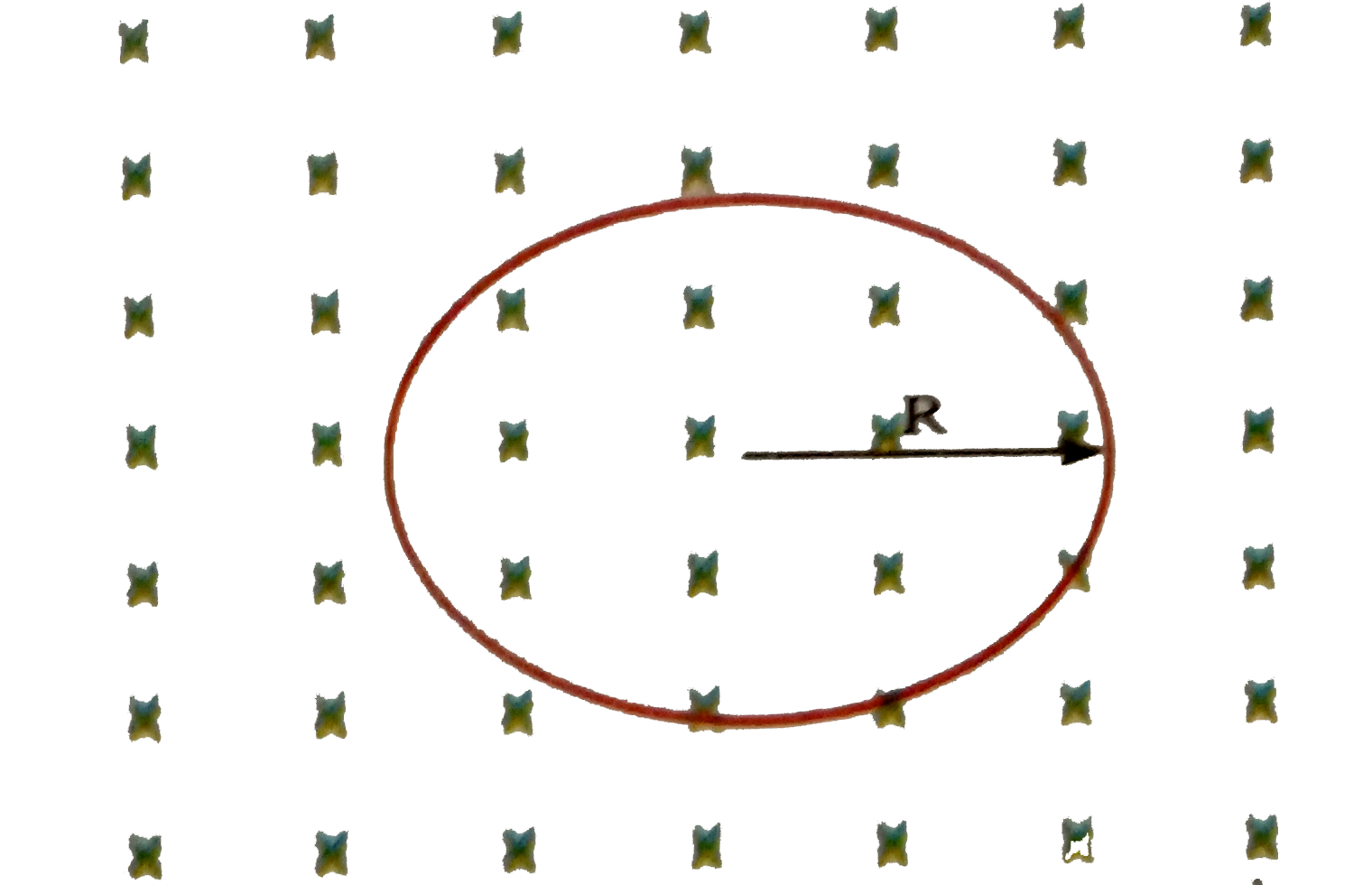
View Solutiona conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View Solution