In Fig. three identical massless springs are kept horizontal. The left end of the first is tied to a wall. The left end of the second spring is tied to a block of mass m placed on rough ground and the ,eft end of the third spring is tied to a block of mass m placed frictionless ground. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extensions in these springs are x1, x2 and x3, respectively. Find the relationship between x1, x2, and x3

The spring force on all springs will be same as springs are ideal. As spring constants of all three springs are same, hence, stretch of all three springs will be equal.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct76videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionA block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (x0) in the spring during the subsequent motion.
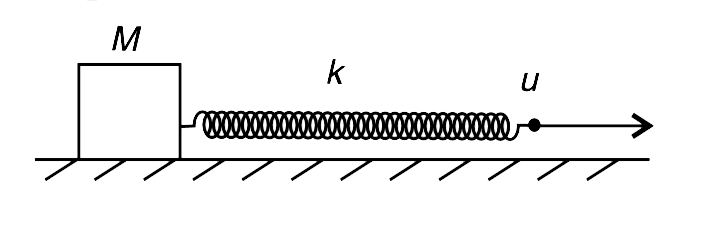 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The left end of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.
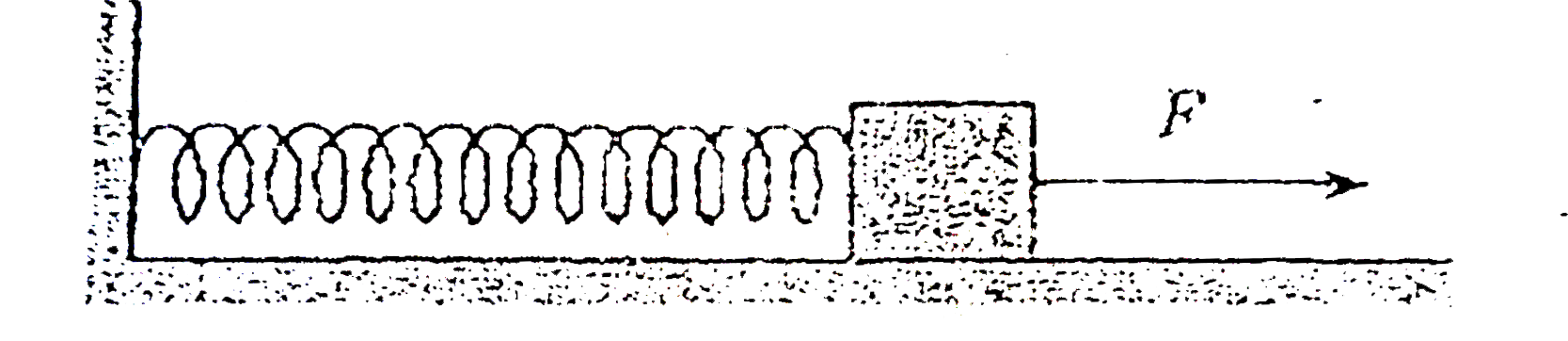
What is the maximum speed of the block in the ensuing motion after the force F is removed?A√FxmB√Fx2mC√2FxmDx√Fm - Question 2 - Select One
The left and of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.

What is the maximum speed of the block in the ensuing motion after the force F is removed?A√FxmB√Fx2mC√2FxmDx√Fm - Question 3 - Select One
Two spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
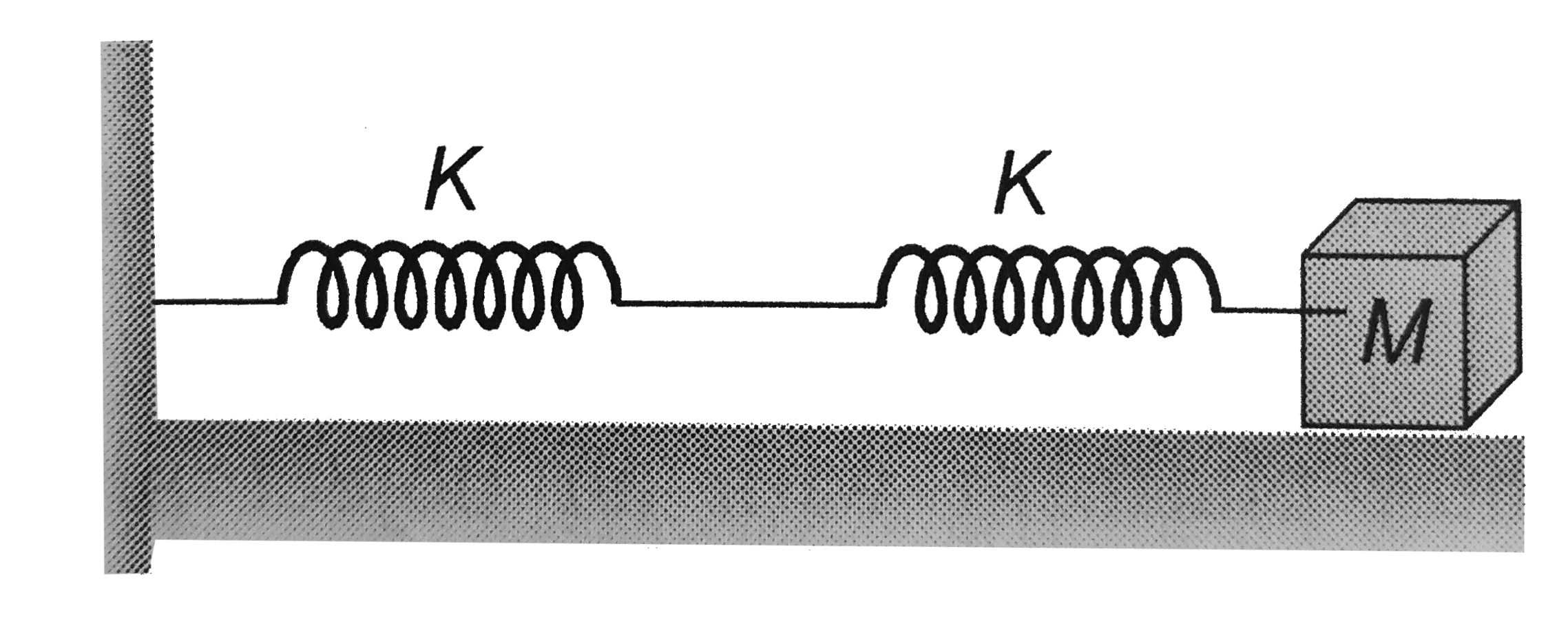 A12π√k2MB12π√kMC12π√2kMD12π√Mk
A12π√k2MB12π√kMC12π√2kMD12π√Mk
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
 View Solution
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
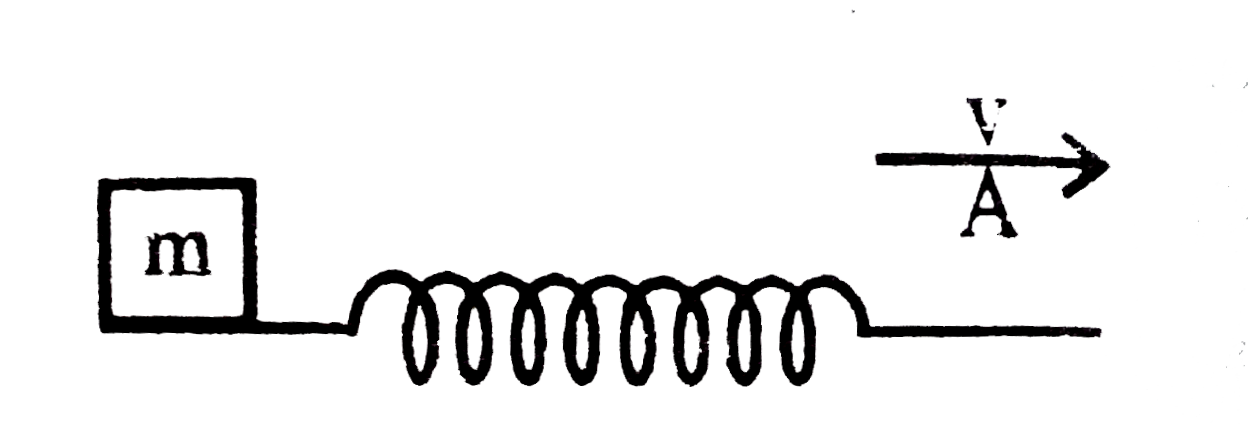 View Solution
View Solution

