In figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is L=√3R. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is ω=VR. Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled (=2√3R).
(a) ![In figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is L = sqrt3R. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is omega = (V)/(R). Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled (= 2 sqrt3 R). (a)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C06_E01_040_Q01.png)
The correct Answer is:34MV2 in both case. In case (b) the Kinetic energy will be higher if length was doubled.
Step by step video, text & image solution for In figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is L = sqrt3R. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is omega = (V)/(R). Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled (= 2 sqrt3 R). (a) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A string is wrapped around a cylinder of radius R and pulled at the top most point horizontally by a force F The cylinder rolls without slipping on the horizontal surface. The work done by the force by the time the cylinder makes one full rotation is
View SolutionA uniform cylinder has radius R and length L. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is mg equal to the moment of inertia of the same cylinder about an axis passing through its centre and normal to its length, then
View Solution
Knowledge Check
A ring performs pure rolling on a horizontal fixed surface with its centre moving with speed v.
AMaximum possible speed that any particle of ring may have is v/√2BMinimum possible speed that any particle of ring may have is v/√2Cparticles on the ring may have speed anywhere between 0 and 2u.DNone of theseA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
AML212BMR24CM[L212+R24]DM[L212+R22]
A cylinder is rolling without slipping on a plank which is also moving with speed 10m/s on a horizontal surface as shown. The speed of centre of the cylinder is 20m/s. The mass of cylinder is 2kg. The kinetic energy of the cylinder when observed from ground is
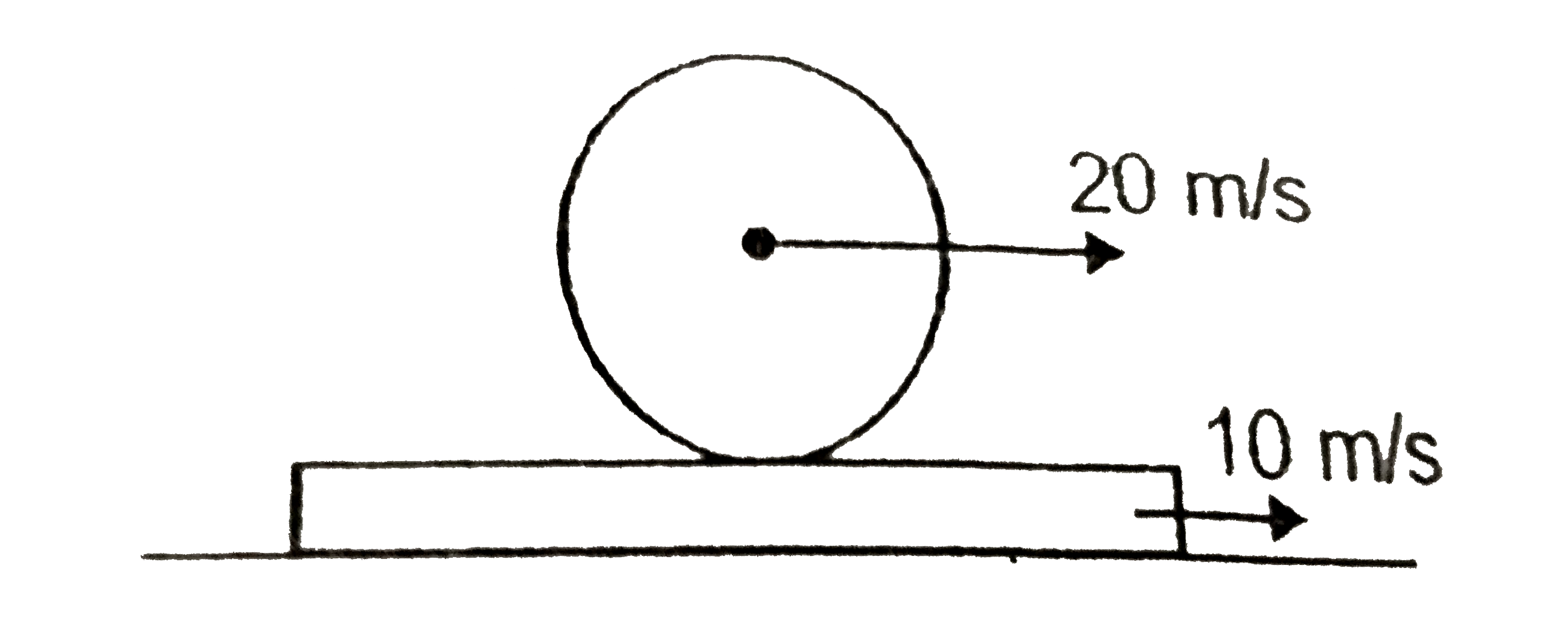
View SolutionA cylinder rolls on a horizontal polane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
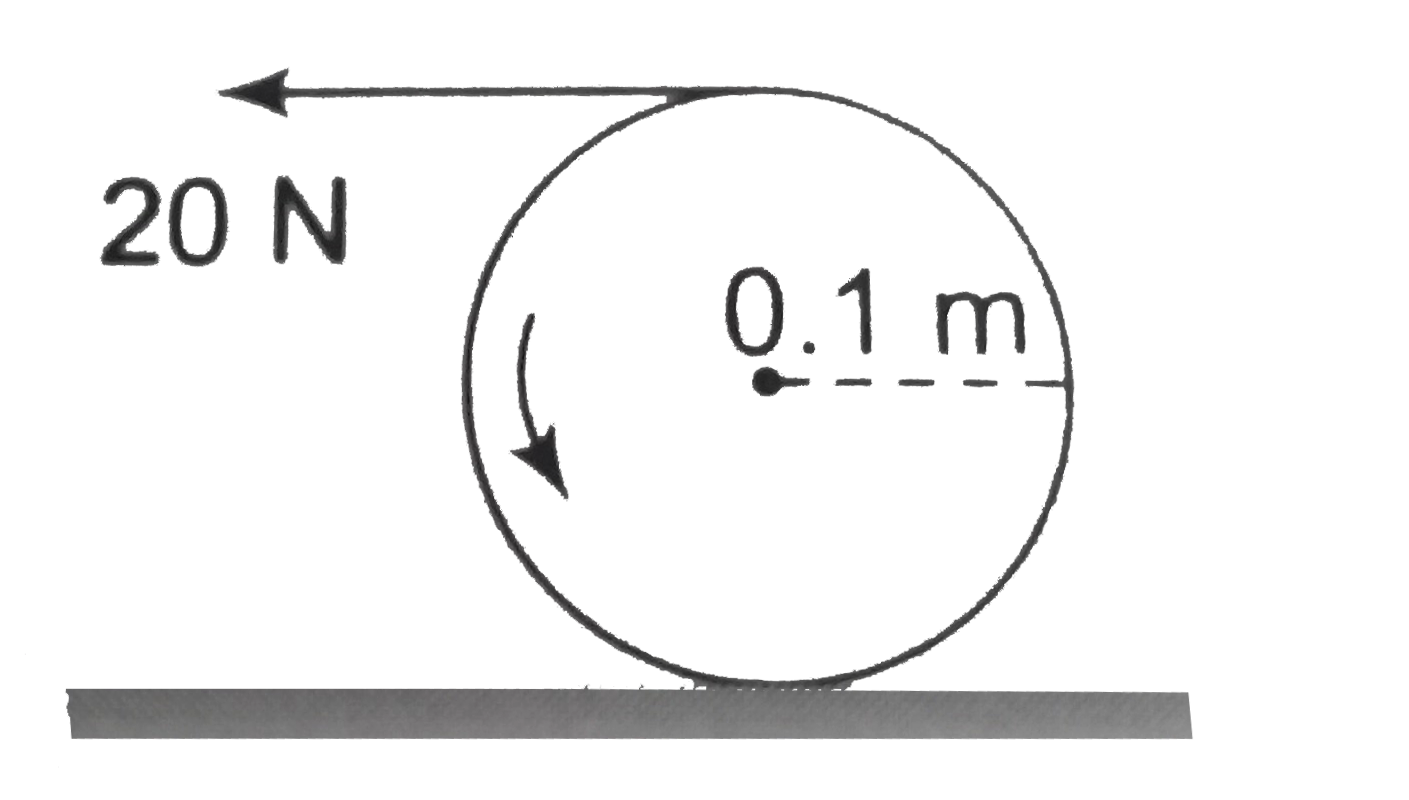 .
.
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View SolutionA solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
View Solution
