There is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
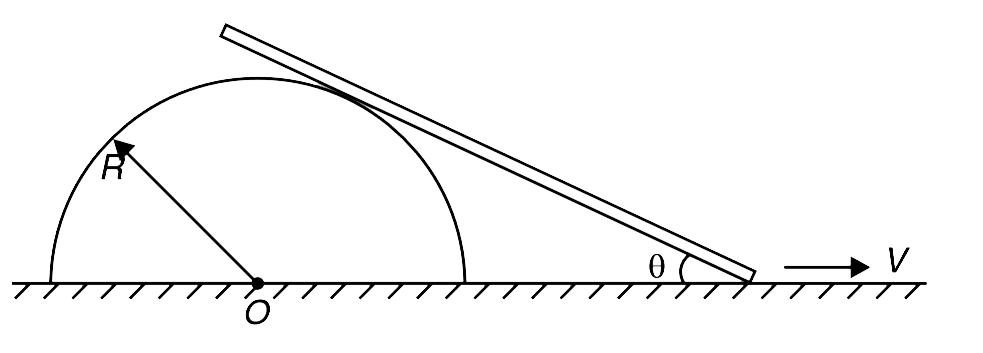
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
The correct Answer is:(a) ω=v2√3R
(b) vy=v4(⏐↓)
Topper's Solved these Questions
Similar Questions
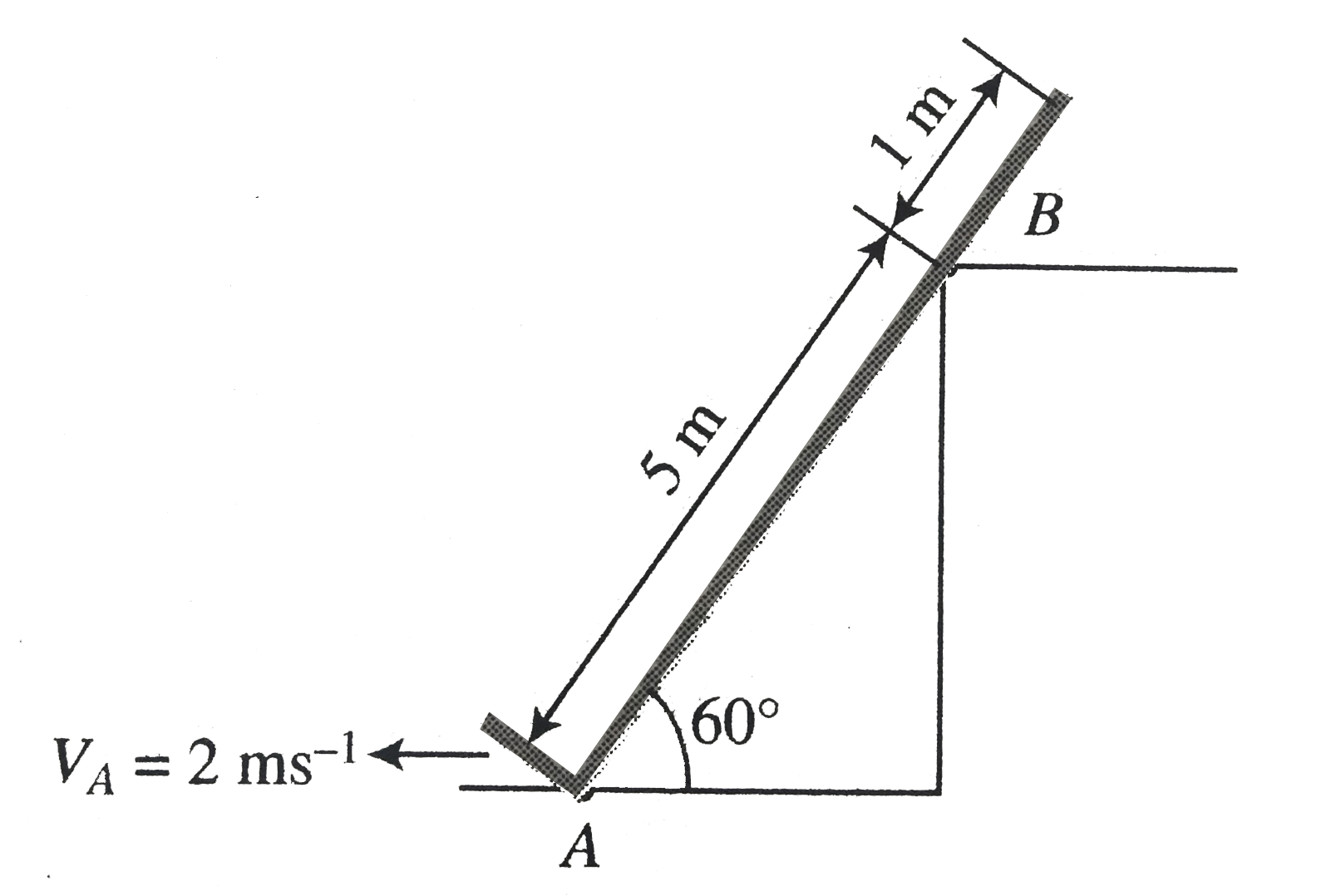
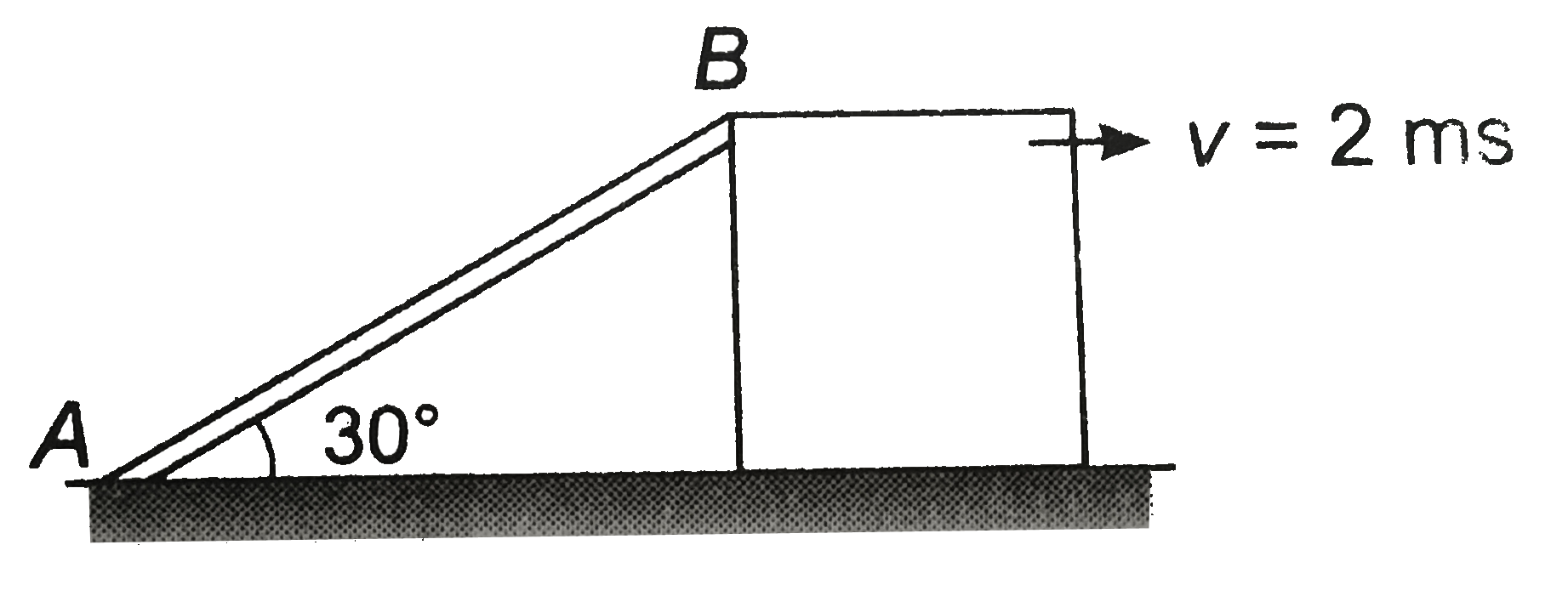
The velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
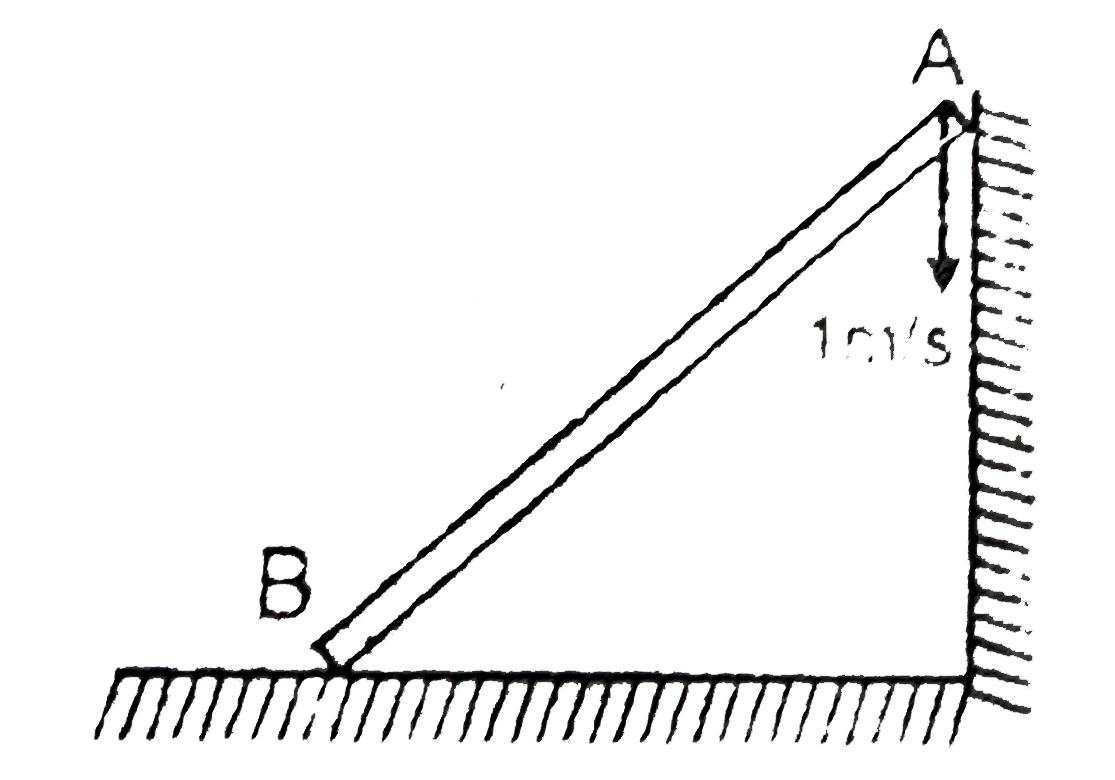
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
View Solution
Knowledge Check
The velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
 A2√3ms−1B1ms−1C12√3ms−1D√32ms−1
A2√3ms−1B1ms−1C12√3ms−1D√32ms−1A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
 A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/sA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224
A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionPoint A of rod AB(l=2m) is moved upwards against a wall with velocity v=2m/s. Find angular speed of the rod at an instant when θ=60∘.
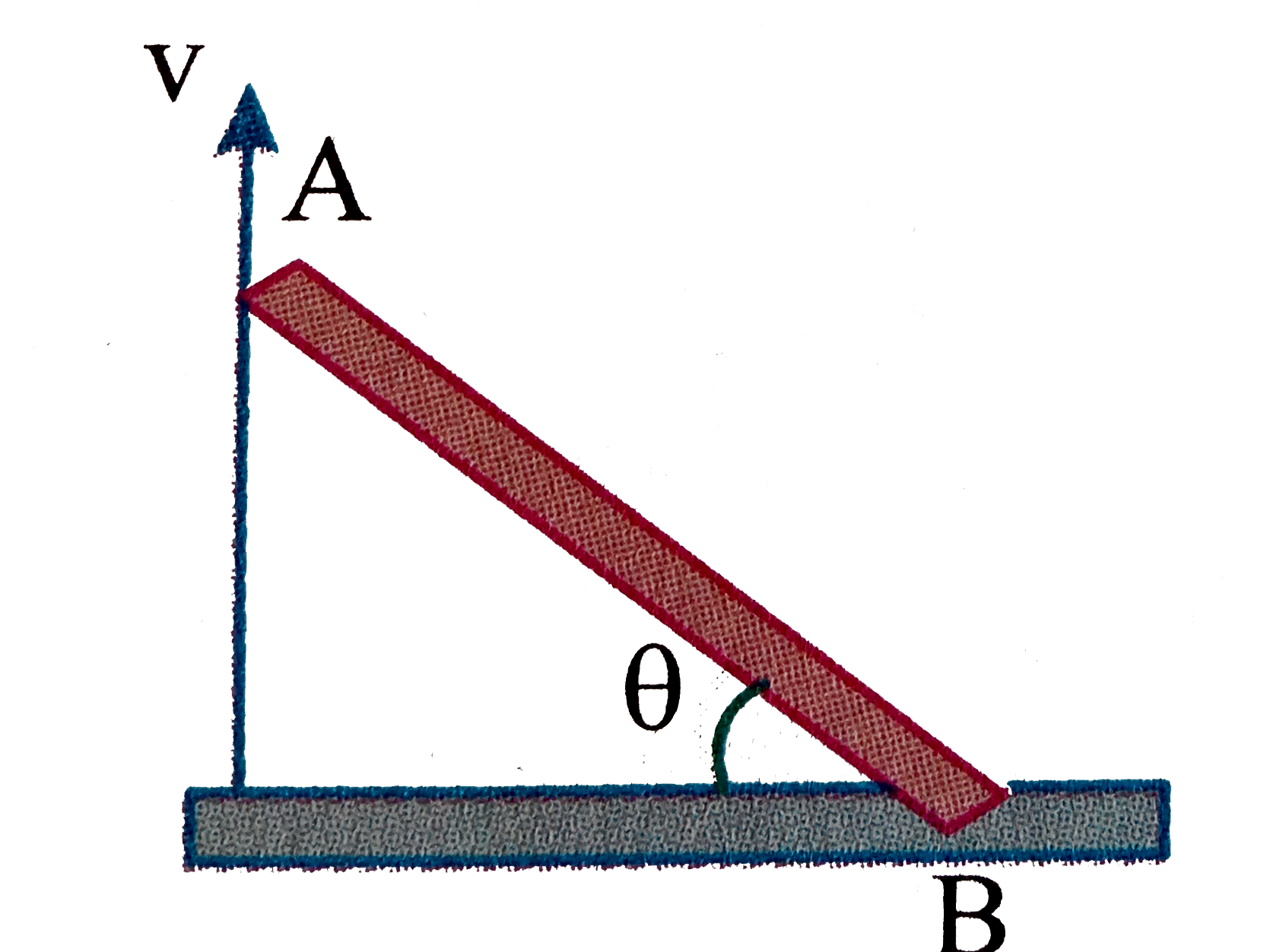
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
View Solution
