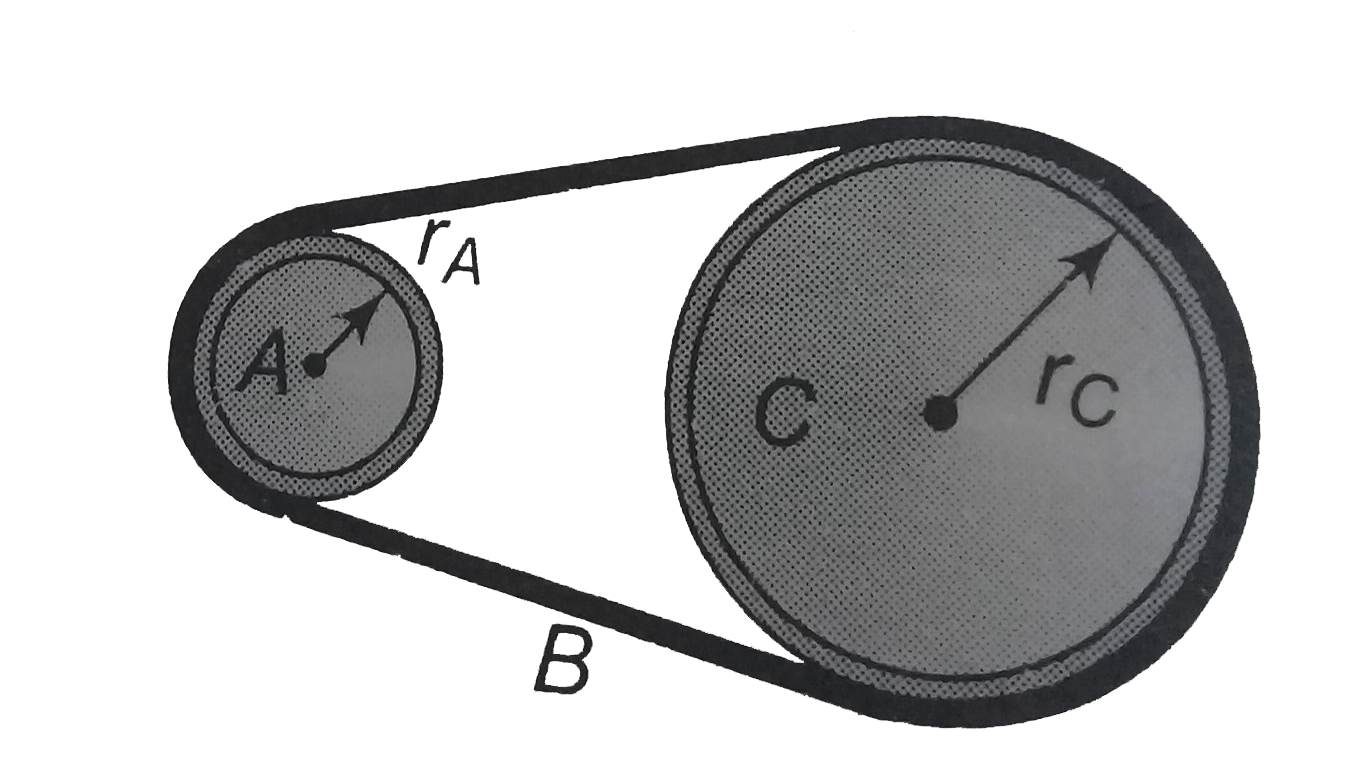
In figure whell A of radius rA=10cm is coupled by belt B to whell C of radius rC=25cm. The angular speed of whell A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for whell C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
 .
.
15 s
12.5 s
20 s
10 s
The correct Answer is:C
( c) If the belt does not slip, the linear speeds at the two rims must be equal. Since the belt does not slip, a point on the rim of wheel C has the same tangential acceleration as a point on the rim of wheel A. This means that ∝ArA=∝CrC. where ∝A is the angular accleration of wheel A and ∝c is the angular acceleration of wheel C . Thus,
∝C=(rArC)∝c=(10cm25cm)(1.6rad/s2)=0.64rad/s2
With the angular speed of wheel C given by ωC=∝Ct,
The time for it to reach an angular speed of ω=100rev/min=10.5rad/s starting from rest is
t=ωC∝C=12.8rad/s0.64rad/s2=20s.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Torque , Torque Equation And Equilibrium Of A Rigid Body29videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia39videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
In Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.
 View Solution
View SolutionWheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of 1.5rads−2 . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
A20 secB10 secC1.5 secD15sec - Question 2 - Select One
A belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
A3.2rad/sB0.32rad/sC20rad/sD0.032rad/s - Question 3 - Select One
The angular speed of a particle,moving in a circle of radius 20 cm ,increases from 2rad/s→40rad/s in 19 s the ratio of its centripetal acceleration to tangential acceleration at the end of 19 s is ,
A400:1B1:800C1:400D800:1
A gridstone has a constant acceleration of 4 rad s−1. Starting from rest, calculate the angular speed of the grindstone 2.5 s later.
View SolutionA gridstone has a constant acceleration of 4rads−1. Starting from rest, calculate the angular speed of the grindstone 2.5 s later.
View SolutionA belt moves over two pulleys A and B as shown in the figure. The pulleys are mounted on two fixed horizontal axles. Radii of the pulleys A and B are 50 cm and 80 cm respectively. Pulley A is driven at constant angular acceleration of 0.8 rad/s2 unitl pulley B acquries an angular velocity of 10 rad/s. The belt does not slide on either of the pulleys.
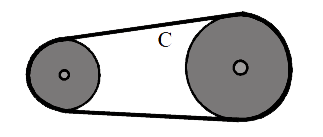
(a)Find the acceleration of a point C on the belt and angular acceleration of the pulley B.
(b) How long does it take for the pulley B to acquire an angular velocity of 10 rad/s ?View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of a radius.View SolutionA circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of 20.0rad/s2. What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
View Solution

