In given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
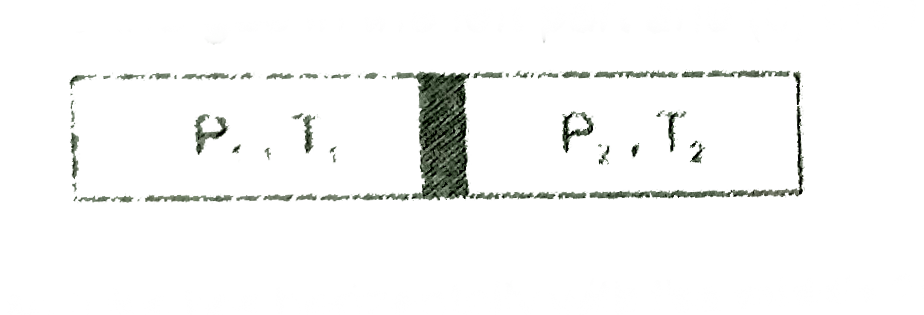Solution in Tamil
For an adiabatic process, PVγ=Constant
So P1Vγ1=P2Vγ2 … (i)
According to the problem
V1+V2=V0
Then the euation (i)
P1Vγ2=P2(V0−V1)γ
or (P1P2)1γ=V0−V1V1
or V1−P1γ1=V0−P1γ2−V1P1γ2
or V1(P1γ1+P1γ2)=V0P1γ2
or V1=P1γ2V0P1γ1+P1γ2
V2=P1γ1V0P1γ1+P1γ2
(b) Since the whole process takes place in adiabatic surroundings, the separator is adiabatic.
Hence heat given to the gas in the left part = 0
(c) There will be a common pressure 'p' when the equilibrium is reached.
P1Vγ1+P2Vγ2=PVγ0
For equilibrium, V1=V2=V02
Hence,
P1(V02)γ+P2(V02)γ=P(V0)γ
P=⎛⎜
⎜⎝P1γ1+P1γ22⎞⎟
⎟⎠γ 
Topper's Solved these Questions
Similar Questions
A wave of wavelength 0.60 cm is produced in air and it travels at a speed of 300 ms^-1. Will it be audible?
07:04View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
16:47View SolutionShow a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
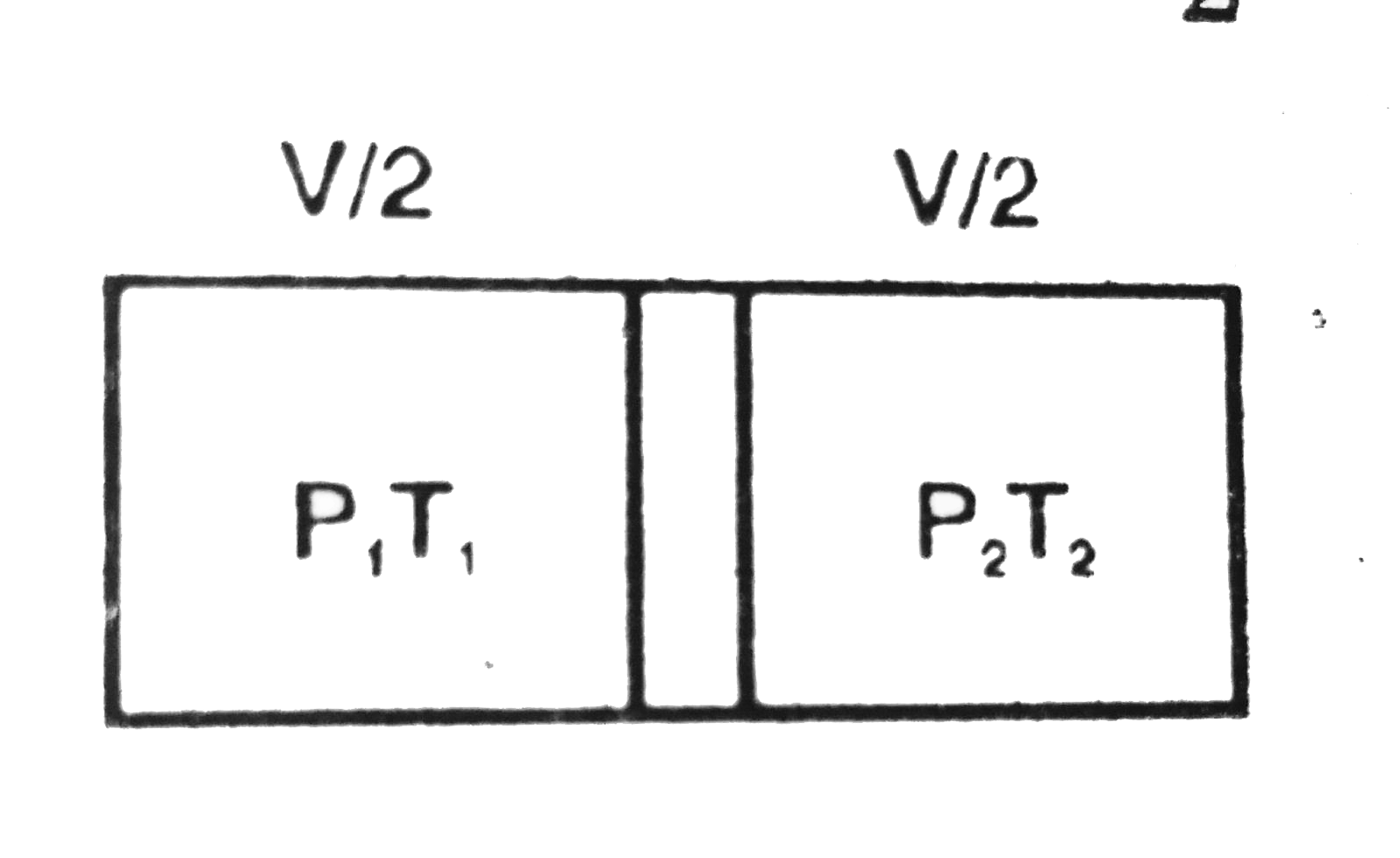
06:54View Solutionshows a cylindrial tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the tempreture are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the tempreture becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium tempreture. (d) how much heat has flown from the gas on the right to the gas on the left ?
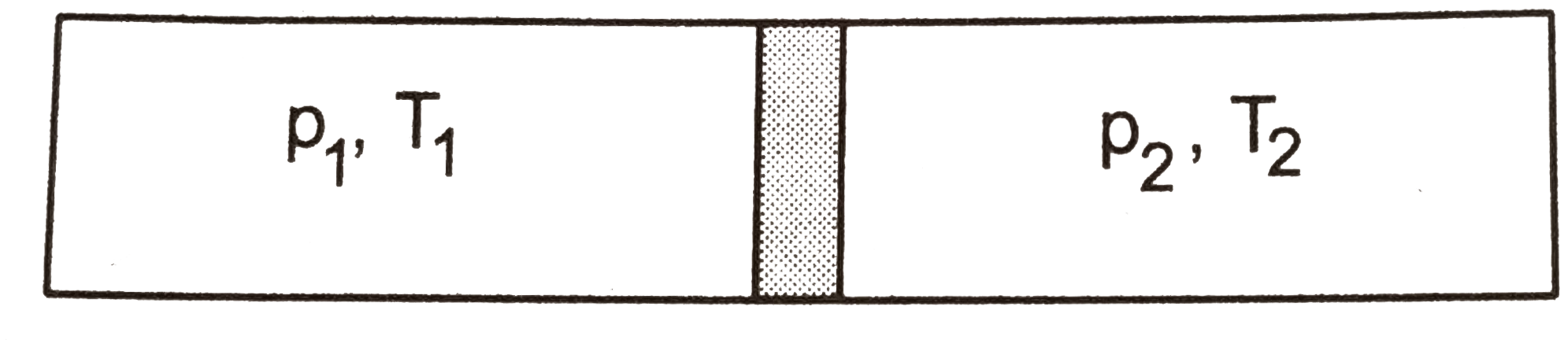
05:05View SolutionFigure shows an adiabatic cylindrical tube of volume (V_0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p_1) and the temperatures (T_1) is injected into the left part and the another ideal gas at pressures (P_2) and temperature (T_2) is injected into the right part. (C_p / C_v = gamma) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.
12:14View SolutionAn adiabatic cylindrical tube is fitted with an adiabatic separator as shown in figure. Initial separator is in equilibrium and divides a tube in two equal parts. The seperator can be slide into the tube by an extermal mechanism. An ideal gas (gamma = 1.5) is injected in the two slides at equal pressure and temperature. Now separator is slid to a piston where it divides the tube in the ratio 7 :3 The ratio of the temperature in the two parts of the vessel is sqrt(n) : sqrt(7) find n .
04:41View SolutionA cylindrical tube with adiabatic walls having volume 2V_(0) contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are P_(0), T_(0) on the left and 2P_(0), 2T_(0) on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal
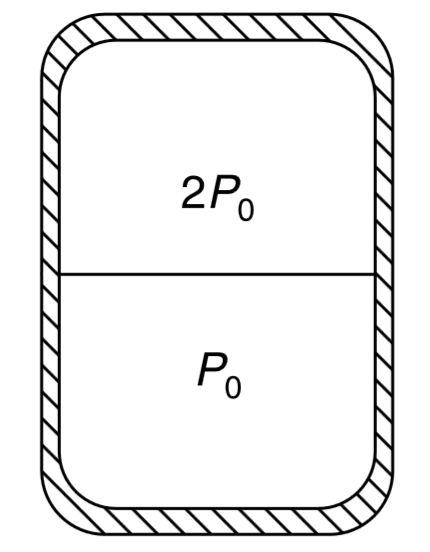
04:47View SolutionA cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
View SolutionFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
View SolutionTwo closed bulb of euqal volume (V) containing an ideal gas initially at pressure p_(i) and Temperature T_(1) are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then released to T_(2) . The final pressure p_(t) is :
03:40View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure P_(i) and temperature T_(1) are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T_(2) . The final pressure P_(f) is :
03:40View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:
08:41View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure P_(1) . The same gas is expanded adiabatically to a volume 2V, the final final pressure is P_(A) . In terms of the ratio of the two specific heats for the gas gamma , the ratio P_(I)//P_(A) is
06:43View SolutionFig shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the temperature becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium temperature. (d) how much heat has flown from the gas on the right to the gas on the left ?
02:50View SolutionFigure shows an adiabatic cylindrical tube of volume (V_0) divided in two parts by a frictionless adiabatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (P_1) and the temperatures (T_1) is injected into the left part and the another ideal gas at pressures (P_2) and temperature (T_2) is injected into the right part. (C_p / C_v = gamma) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.
08:30View Solution