A cylindrical tube with adiabatic walls having volume 2V0contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are P0,T0 on the left and 2P0,2T0 on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal

Find work done by the gas on the right part?
Find the final pressure on the two sides
Find the final equilibrium temperature
How much heat has flows from the gas on the right to the gas on the left?
The correct Answer is:A, B, C, D
(a) As change in volume ΔV=0
∴ Work done by gas on right part =∫pdV=0
(b) and (c ) Due to adiabatic walls, no heat transfer form cylindrical tube.
U1+U2=U1+U2
32n1RT1+32n2RT2=32n1RT+32n2RT

T=n1T1+n2T2n1+n2
=(P0V0)T0RT0+2P0(V0)2T0R(2T0)P0V0RT0+2P0V0R(2T0)=3T02
From mole conservation
P0(V0)RT0=P1(V0)RT⇒p'=3P02
⇒ similarly p'2=3P02
(d) Heat flow form the gas right to left.
Q=ΔU+W(∵W=0)
Q=ΔU=32n1R(T−T1)
=32P0V0RRT0(3T02−T0)=3P0V04
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
65 Videos
Similar Questions
shows a cylindrial tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the tempreture are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the tempreture becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium tempreture. (d) how much heat has flown from the gas on the right to the gas on the left ?
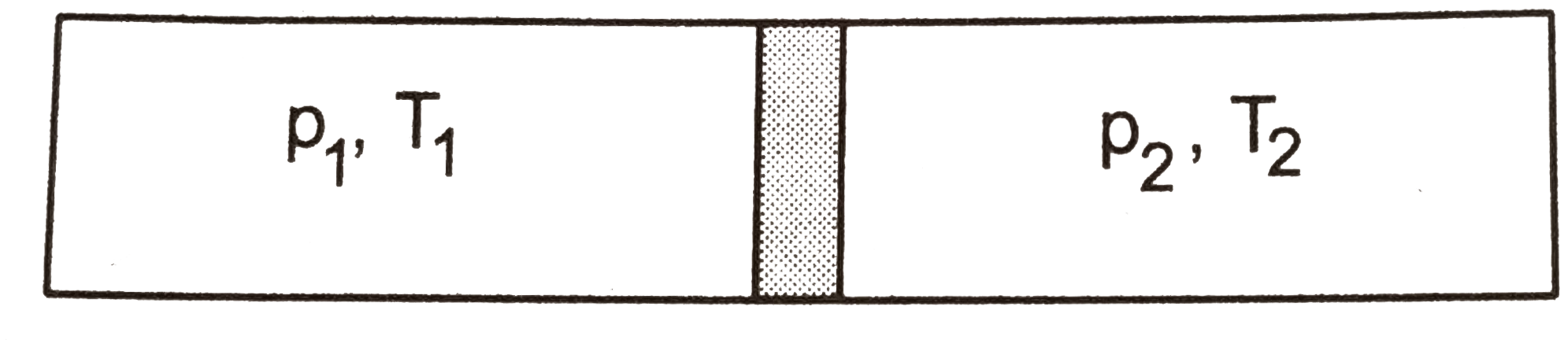
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
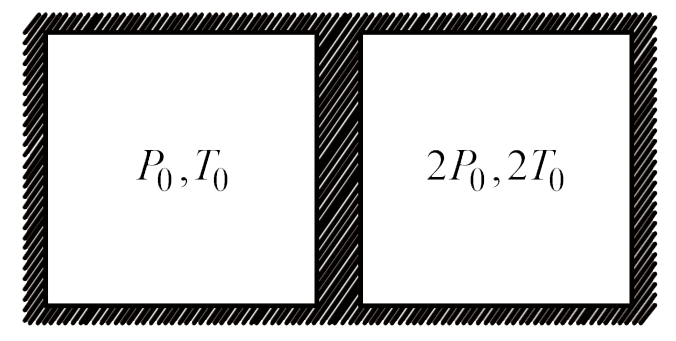
The pressure in left compartment after thermal equilibrium is achieved is
View Solution
Knowledge Check
A uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
AThe number of moles of the gas in the tube is PVRTln2BThe number of moles of the gas in the tube is PVRTln4CThe internal energy of the gas in the tube is (3/2)PVDThe internal energy of the gas in the tube is (3/2)nRT.If 2 mol of an ideal monatomic gas at temperature T0 are mixed with 4 mol of another ideal monatoic gas at temperature 2T0 then the temperature of the mixture is
A53T0B32T0C43T0D54T0In an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
A35B53C25D52
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

The heat that flown from right compartment to left compartment before thermal equilibrium is achieved is
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

If the pin which was keeping the piston fixed is removed and the piston is allowed to slide slowly such that a state of mechanical equilibrium is achieved. The volume of left compartment when piston is in equilibrium is
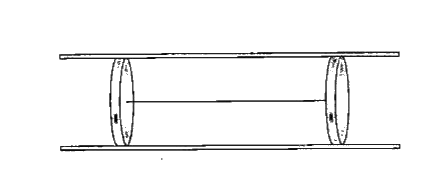
View SolutionA cylindrical tube ofuniform cross sectional area A is fitted with two frictionless pistons, as shown in figure-2.46. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is equal to atmospheric pressure P0 and temperature isT0. If the temperature of the gas is increased to 2T0, find the tension in the wire.
View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
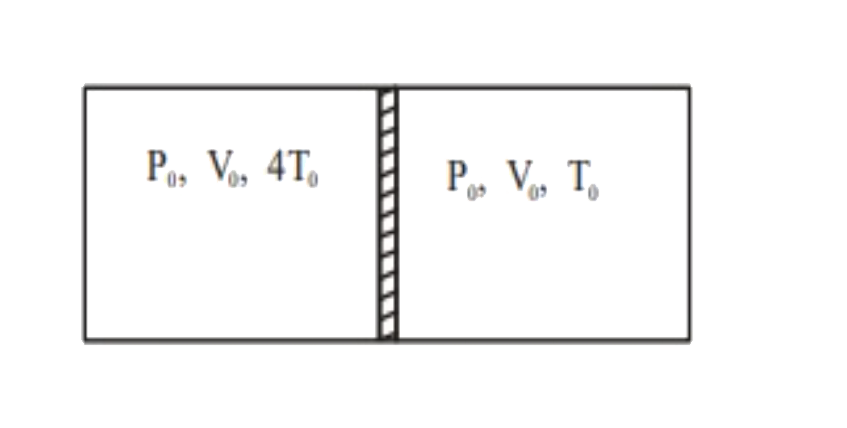
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is cthe cross-sectional are of the cylinder. at this time, the temperature of the gas has become.

View Solution
